
第三节平面及其方程曲面方程与空间曲线方程的概念平面的点法式方程平面的一般方程两平面的夹角■小结思考题
第三节 平面及其方程 ◼ 曲面方程与空间曲线方程的概念 ◼ 平面的点法式方程 ◼ 平面的一般方程 ◼ 两平面的夹角 ◼ 小结 思考题

一、曲面方程与空间曲线方程的概念曲面的实例水桶的表面、台灯的罩子面等曲面在空间解析几何中被看成是点的儿何轨迹F(x,y,z) = 0曲面方程的定义如果曲面S与三元方程SF(x,y,z)= 0有下述关系:(1)曲面S上任一点的坐标都满足方程;0x(2)不在曲面S上的点的坐标都不满足方程;那么,方程F(x,y,z)=0就叫做曲面S的方程而曲面S就叫做方程的图形
一、曲面方程与空间曲线方程的概念 水桶的表面、 曲面在空间解析几何中被看成是点的几何轨迹. 曲面方程的定义 曲面的实例 (1) 曲面S上任一点的坐标都满足方程; (2) 不在曲面S上的点的坐标都不满足方程; 如果曲面S F(x, y,z) = 0 有下述关系: 那么, 方程F(x, y,z) = 0 就叫做曲面S的方程, 而曲面S就叫做方程的图形. 台灯的罩子面等. 与三元方程 x y z O S F(x, y,z) = 0
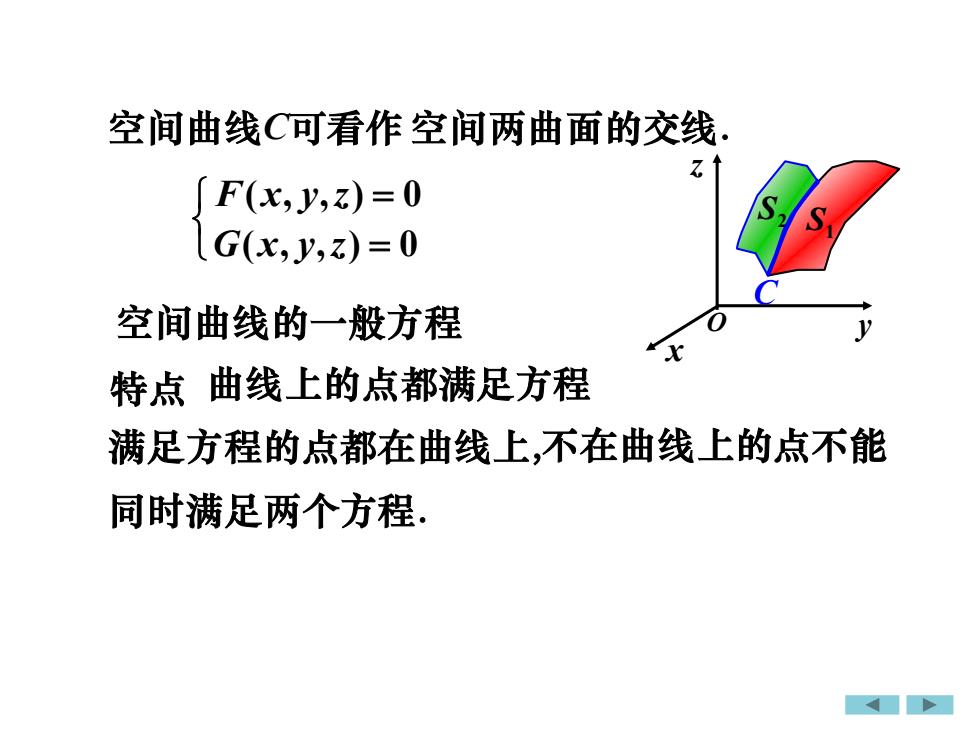
空间曲线C可看作空间两曲面的交线Z[F(x,y,z) = 0?S[G(x,y,z) = 0空间曲线的一般方程VX特点曲线上的点都满足方程满足方程的点都在曲线上,不在曲线上的点不能同时满足两个方程
空间曲线的一般方程 空间曲线C可看作 特点 曲线上的点都满足方程 满足方程的点都在曲线上,不在曲线上的点不能 同时满足两个方程. 空间两曲面的交线. x y z O S1 S2 C F(x, y,z) = 0 G(x, y,z) = 0

二、平面的点法式方程1如果一非零向量垂直于一平面,这向量就叫做该平面y的法线向量(法向量)法线向量的特征:垂直于平面内的任一向量一块平面可以有许多法向量。已知 n=(A,B,C),M.(xo, yo, zo)设平面上的任一点为 M(x,J,z)必有 M,Mln= M,M.n=0
x y z O n 如果一非零向量垂直于 法线向量的特征:垂直于平面内的任一向量. 已知 n = (A, B, C), ( , , ) 0 0 0 0 M x y z 设平面上的任一点为 M(x, y, z) M M n 必有 0 ⊥ M0M n = 0 二、平面的点法式方程 一块平面可以有许多法向量. M0 • M • 一平面,这向量就叫做该平面 的法线向量(法向量)
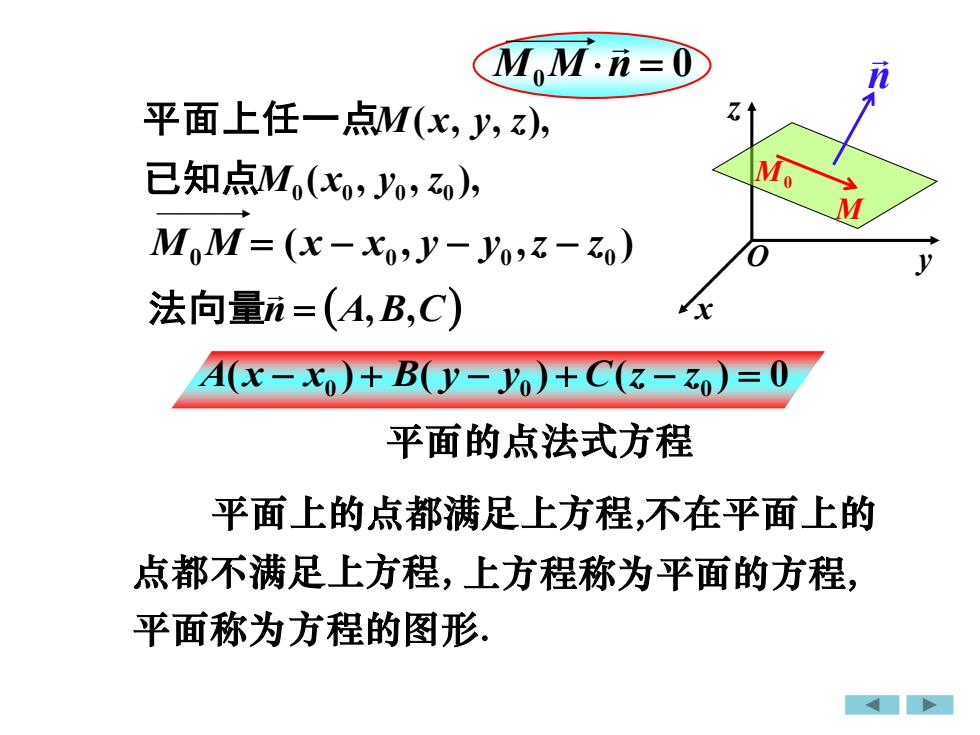
M.M.n=0nZt平面上任一点M(xy,z)M.已知点M.(xo,yo,zo),MM,M= (x-xo,y-yo,z- zo)0V法向量n=(A,B,C)XA(x - x) + B(y- yo)+ C(z - zo)= 0平面的点法式方程平面上的点都满足上方程,不在平面上的点都不满足上方程,上方程称为平面的方程平面称为方程的图形
x y z M0M = O 平面的点法式方程 平面称为方程的图形. n = (A,B,C) 法向量A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0 n M0 M 平面上的点都满足上方程,不在平面上的 点都不满足上方程, 上方程称为平面的方程, M0M n = 0 ( , , ), 0 0 0 0 已知点M x y z 平面上任一点M(x, y, z), ( , , ) 0 0 0 x − x y − y z − z