
第四节空间直线及其方程空间直线的一般方程空间直线的对称式方程与参数方程两直线的夹角直线和平面的夹角小结思考题
第四节 空间直线及其方程 ◼ 空间直线的一般方程 ◼ 空间直线的对称式方程与参数方程 ◼ 两直线的夹角 ◼ 直线和平面的夹角 ◼ 小结 思考题

空间直线的一般方程I定义空间直线可看成两平面的交线II: Ax+By+Cz+D =0z.ⅡII, : A,x+ B,J+C,z+ D, = 0ⅡAx+ By+Ciz + D, = 0L10yAx+B,y+C,z+D, = 0x空间直线的一般方程注(1)A、B、C与A、B,、C,不成比例;(2)直线L的一般方程形式不是唯一的
1 2 定义 空间直线可看成两平面的交线. 1 : A1 x + B1 y + C1 z + D1 = 0 2 : A2 x + B2 y + C2 z + D2 = 0 + + + = + + + = 0 0 2 2 2 2 1 1 1 1 A x B y C z D A x B y C z D 空间直线的一般方程 一、空间直线的一般方程 L 注 (1) ; A1、B1、C1与A2、B2、C2不成比例 (2) 直线L的一般方程形式不是唯一的. x y z O L
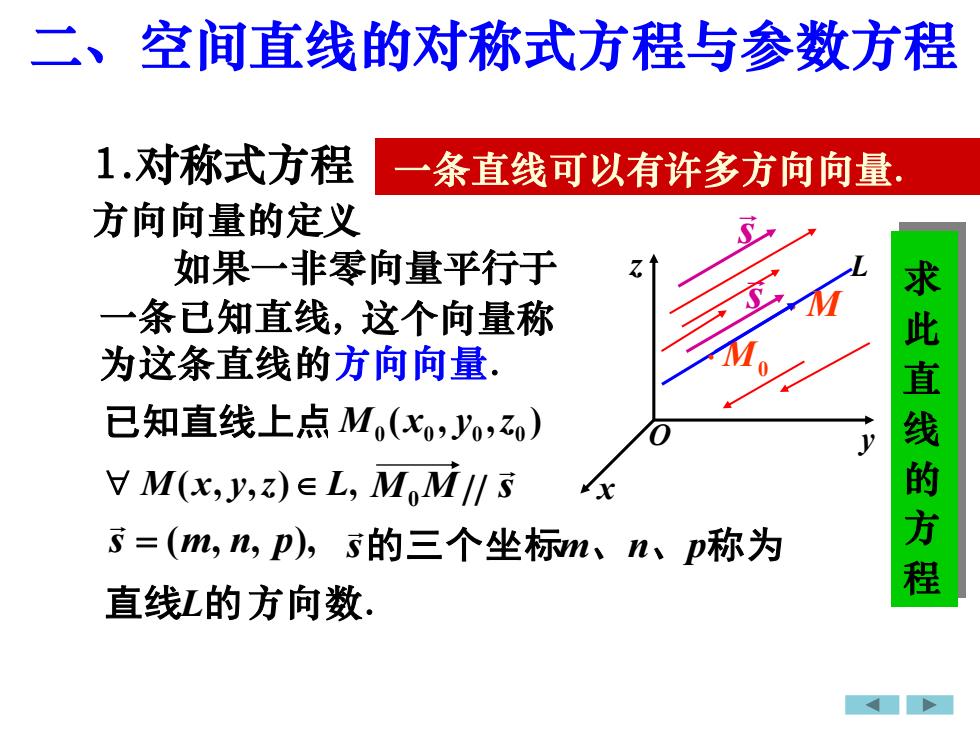
二、空间直线的对称式方程与参数方程1.对称式方程一条直线可以有许多方向向量方向向量的定义如果一非零向量平行于求此直线的方程M一条已知直线,这个向量称M为这条直线的方向向量已知直线上点M.xo,yo,zo)yV M(x,y,z)e L, M,M// s=(m,n,p), s的三个坐标m、n、p称为直线L的方向数
方向向量的定义 如果一非零向量平行于 s L 已知直线上点 M0 M M(x, y,z) L, M M s 0 // s = (m, n, p), 二、空间直线的对称式方程与参数方程 1.对称式方程 一条直线可以有许多方向向量. 求 此 直 线 的 方 程 一条已知直线, 这个向量称 为这条直线的方向向量. ( , , ) 0 0 0 0 M x y z 直线L的 s的三个坐标m、n、p称 为 s 方向数. x y z O

因为 M,M=(x-Xo,-yo,z- zo)故M,MI/ →x-xoZ-Zoy-yo直线的对称式方程nmp(点向式、标准式)x-xoZ- Zoy-yomnpx=xo +mt直线的参数方程y= yo +nt故z = zo + pt直线方程的几种形式可以互相转换
p z z n y y m x x0 0 − 0 = − = − 直线的对称式方程 p z z n y y m x x0 0 − 0 = − = − 令 直线的参数方程 ( , , ) 0 0 0 0 因为 M M = x − x y − y z − z 故 M M s 0 // 故 直线方程的几种形式可以互相转换. (点向式、标准式) = t x = x + mt 0 y = y + nt 0 z = z + pt 0

x-xo_y-yo_z-zo过两点作直线mnD例1 求过两点M,(1,2,3),M2(2,6,5)的直线方程解向量M,M,与直线平行M2取 s =M,M, =(1,4,2)M,所求直线方程为z-3x-1y-2142
例1 解 取 所求直线方程为 = − 1 x 1 p z z n y y m x x0 0 − 0 = − = − ·M1 ·M2 s 求过两点M1 (1,2,3),M2 (2,6,5)的直线方程. 向量 M1M2 与直线平行 s = (1,4,2) M1M2 = = − 4 y 2 2 z − 3 过两点作直线