北京工业大学：《概率与数理统计》课程教学资源（PPT课件讲稿）§3.1 二维随机向量及其分布函数 §3.2 二维离散型随机向量 §3.3 二维连续型随机向量

说明 由上面的几何解释， 易见：随机点(X,Y)落在矩 形区域： x1x≤x2,y1y≤y2 内的概率为 P{x1<X≤2，Jy12} =Fc2,y2)广Fc2,y1)厂Fc1,Jy2+Fc1,Jy1) @@网

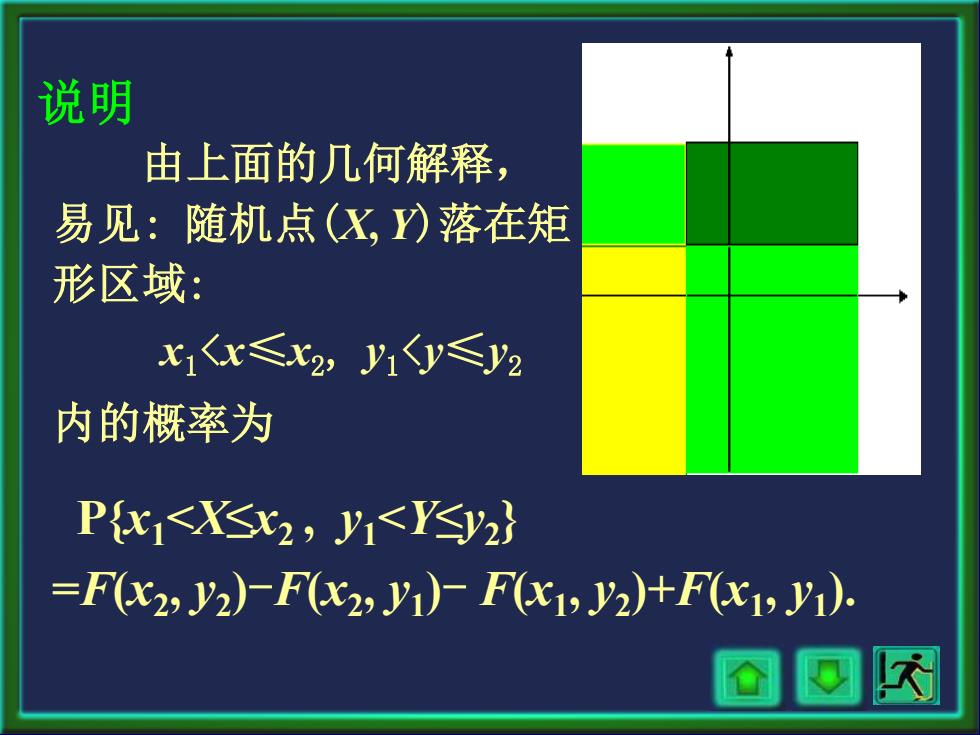
由上面的几何解释， 易见: 随机点(X, Y)落在矩 形区域: x1<x≤x2, y1<y≤y2 内的概率为 P{x1<X≤x2 , y1<Y≤y2 } =F(x2 , y2 )-F(x2 , y1 )- F(x1 , y2 )+F(x1 , y1 ). 说明

二维分布函数Fx,y)的三条基本性质 (1).F化，y)是变量x,y的非减函数； 即yeR给定，当x1<x2时， F(1,y)<F(x2,y). 同样，VxeR给定，当y2时， F(x,y )<F(x,y2). (2).x,y∈R,有0≤Fx,y)≤1； @四的

二维分布函数 F(x, y)的三条基本性质 (1).F(x, y)是变量 x,y 的非减函数； 即  yR给定，当 x1< x2 时， F(x1 , y)≤F(x2 , y). 同样, xR 给定，当y1≤y2时, F(x, y1 )≤F(x, y2 ). (2).x, yR, 有 0≤F(x, y)≤1；

(3).Vy∈R,F(-0,y)=0, Vx∈R,Fx,-oo=0, F(-00,-0o=0,F(0,o)=1. 其中 F(-o,y)=lim F(x,y), ●0 F(x,-oo)=lim F(x,y), F(-o,-∞)=，liF(x,y)， Y,V->-c0 F(o,o)=m.Fx,)

(3).  yR, F(-∞, y)=0，  xR, F(x, -∞)=0， F(-∞, -∞)=0，F(∞, ∞)=1. ( , ) lim ( , ). ( , ) lim ( , ) , ( , ) lim ( , ), ( , ) lim ( , ) , , , F F x y F F x y F x F x y F y F x y x y x y y x → →− →− →−   = − − = − = − = 其中

§3.2三维离散型随机向量 如果随机向量X,)的每个分量都是离 散型随机变量，则称X,)是二维离散型随 机向量。 二维离散型随机向量X,)所有可能取 的值也是有限个，或可列无穷个

§3.2 二维离散型随机向量 如果随机向量 (X, Y) 的每个分量都是离 散型随机变量，则称 (X, Y) 是二维离散型随 机向量。 二维离散型随机向量(X, Y) 所有可能取 的值也是有限个，或可列无穷个

离散型随机变量 离散型随机向量 X的概率分布： X,)的联合概 率分布： P(X=xk)=Pk> P(X=x,Y=yjPu k=1,2, i,j=1,2, Pk≥0，k=1,2, p,≥0,1，j=1,2,. ∑Σp,=1

离散型随机变量 X 的概率分布: =  = = 1,2, ( ) , kP X x k p k  =  = k k k p p k 1. 0, 1,2, 离散型随机向量 (X, Y) 的联合概 率分布: , 1 , 2 , . ( , ) , = = = = i j P X x i Y y j pi j  =  = i j i j i j p p i j 1. 0, , 1,2,