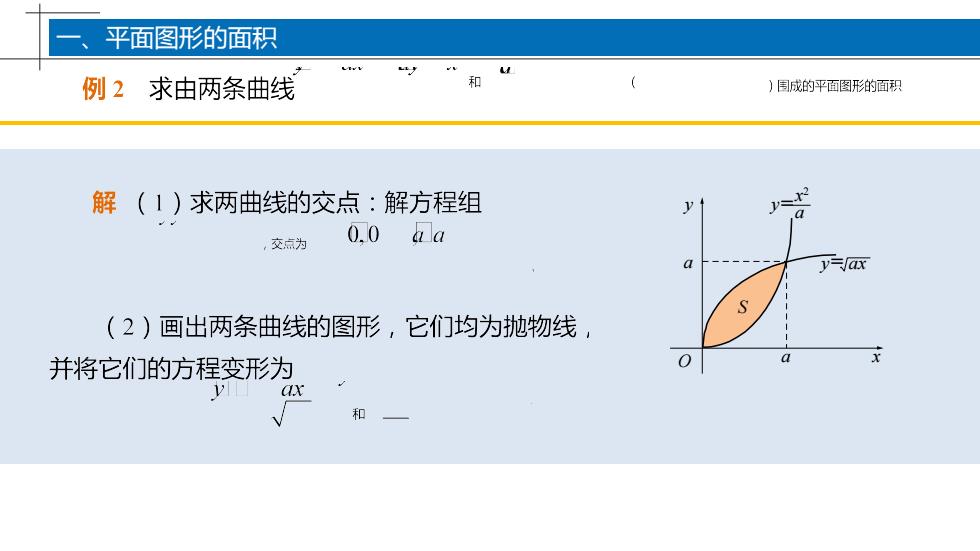
平面图形的面积u和例2求由两条曲线)周成的平面图形的面积x解(1)求两曲线的交点:解方程组yQ0.0dla交点为y-ax0S(2)画出两条曲线的图形,它们均为抛物线,xa0并将它们的方程变形为Vax和
11 S y= ax y O x a a y= x 2 a 一、平面图形的面积

平面图形的面积uyu/1和例2求由两条曲线)围成的平面图形的面积(3)求面积:利用平面图形求面积公式,有
12 一、平面图形的面积

平面图形的面积A萼直线求抛物线例3所围成的平面图形的面积解求曲线与直线的交点,即解方程组yt3y2=2xA(8,4),得与S2V=-x-4S:(D, 4)P, )故交点为和OB(2,-2)若选择为积分变量,则该平面图形视为主两部分2Cx.和组成,并将抛物线方程变形为,则由求平面图形面积的公式,有
13 y 2=2x y=x-4 O x y S1 S2 4 B(2,-2) A(8,4) 一、平面图形的面积

平面图形的面积考百线X例3求抛物线所围成的平面图形的面积dPx4)2Jdd7SS
14 一、平面图形的面积
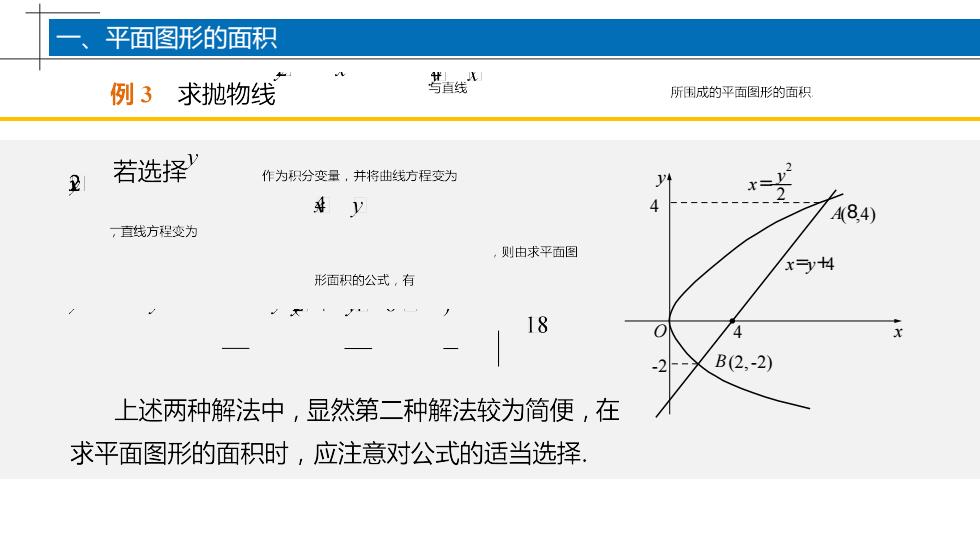
平面图形的面积H.JX与直线求抛物线例3所围成的平面图形的面积若选择"2作为积分变量,并将曲线方程变为y422#y4A(8,4)直线方程变为则由求平面图x14形面积的公式,有118x04B(2,-2)-2上述两种解法中,显然第二种解法较为简便,在求平面图形的面积时,应注意对公式的适当选择
15 4 4 A(8,4) B(2,-2) -2 x=y+4 x= y 2 2 O x y 一、平面图形的面积