
导期 二、双曲线的定义及标准方程 【问题思考】 1定义:一般地,如果F,F2是平面内的两个定点,是一个正常 数,且2<FF2,则平面上满足PF-PF2=2的动点P的轨迹 称为双曲线 2.标准方程: (>0,b>0), (>0,b>0), 3.离心率e-e∈
导航 二、双曲线的定义及标准方程 【问题思考】 1.定义:一般地,如果F1 ,F2是平面内的两个定点,a是一个正常 数,且2a<|F1F2 |,则平面上满足||PF1 |-|PF2 ||=2a的动点P的轨迹 称为双曲线. 2.标准方程: 𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃𝟐 =1(a>0,b>0),𝒚 𝟐 𝒂𝟐 − 𝒙 𝟐 𝒃𝟐 =1(a>0,b>0). 3.离心率 e= 𝒄 𝒂 ,e∈(1,+∞)

导航 4双曲线若-二-1a>,b0的渐近线方程为 双曲线器-三1a@b0的渐近线方程为 5做一做:若双曲线号-二-1>0b0)的焦点到其海近线的 距离等于实轴长,则其离心率e= 答案:√5
导航 4.双曲线𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃 𝟐 =1(a>0,b>0)的渐近线方程为 y=± 𝒃 𝒂 x ; 双曲线𝒚 𝟐 𝒂𝟐 − 𝒙 𝟐 𝒃 𝟐 =1(a>0,b>0)的渐近线方程为 y=± 𝒂 𝒃 x . 5.做一做:若双曲线𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃𝟐 =1(a>0,b>0)的焦点到其渐近线的 距离等于实轴长,则其离心率 e= . 答案: 𝟓

导航 三、抛物线的定义及标准方程 【问题思考】 1.定义:一般地,设F是平面内的一个定点,是不过点F的一条 定直线,则平面上到F的距离与到的距离相等的点的轨迹称 为抛物线
导航 三、抛物线的定义及标准方程 【问题思考】 1.定义:一般地,设F是平面内的一个定点,l是不过点F的一条 定直线,则平面上到F的距离与到l的距离相等的点的轨迹称 为抛物线
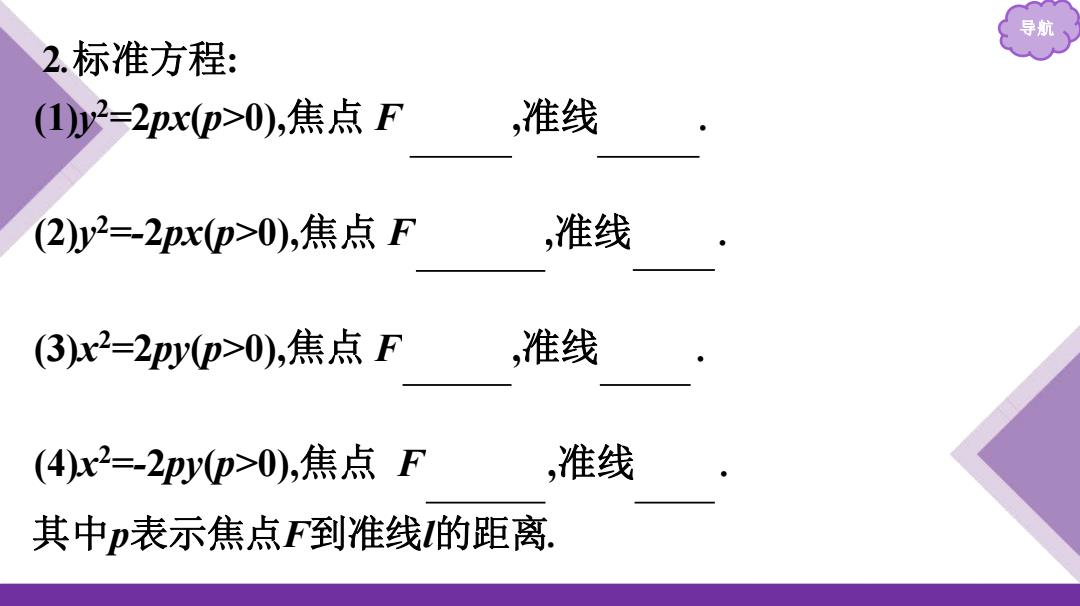
导航 2.标准方程: (1)y2=2px(p>0),焦点F ,准线 (2y2=-2px(D>0),焦点F ,准线 (3)x2=2pyp>0),焦点F ,准线 (4)x2=-2pyp>0),焦点F ,准线 其中p表示焦点F到准线的距离
导航 2.标准方程: (1)y 2 =2px(p>0),焦点 F 𝒑 𝟐 ,𝟎 ,准线 x=- 𝒑 𝟐 . (2)y 2 =-2px(p>0),焦点 F - 𝒑 𝟐 ,𝟎 ,准线 x= 𝒑 𝟐 . (3)x 2 =2py(p>0),焦点 F 𝟎, 𝒑 𝟐 ,准线 y=- 𝒑 𝟐 . (4)x 2 =-2py(p>0),焦点 F 𝟎,- 𝒑 𝟐 ,准线 y= 𝒑 𝟐 . 其中p表示焦点F到准线l的距离

导航 3.做一做:若抛物线y2=-2px的准线经过点(2,2),则该抛物线的 焦点坐标为 答案:(-2,0)
导航 3.做一做:若抛物线y 2=-2px的准线经过点(2,2),则该抛物线的 焦点坐标为 . 答案:(-2,0)