
非线性方程的近似解法 ·迭代法收敛性例题 ·一种迭代加速方法一埃特全方法 ·牛顿迭代法 ·孩截法
非线性方程的近似解法 • 迭代法收敛性例题 • 一种迭代加速方法—埃特金方法 • 牛顿迭代法 • 弦截法
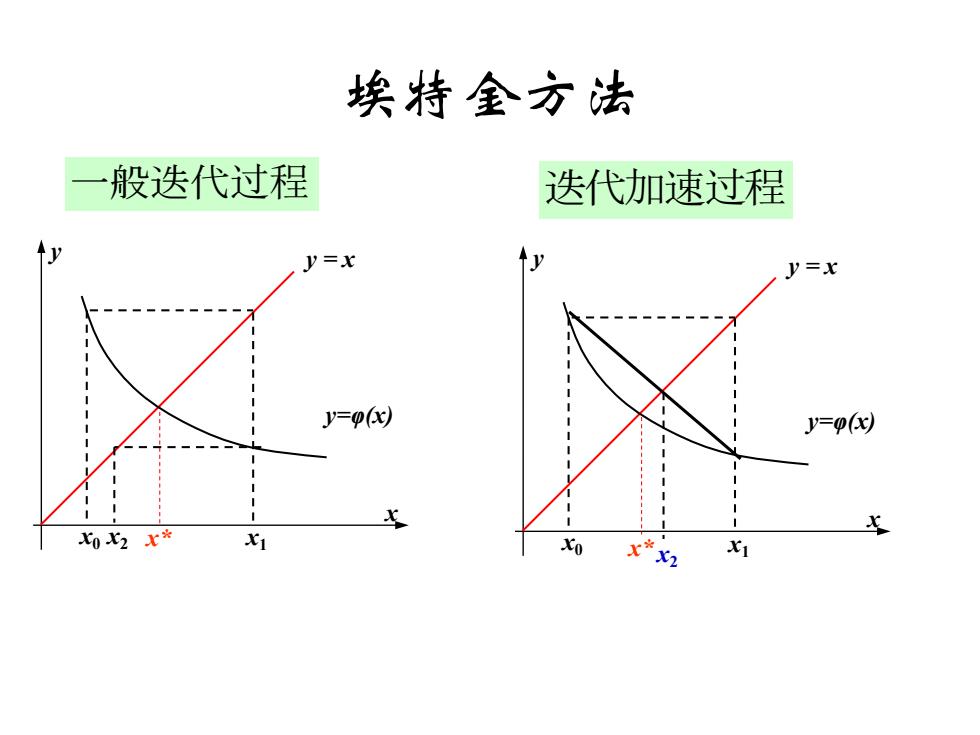
埃特全方法 般迭代过程 迭代加速过程 y=x y=x y=o(x) y=p() 02x* 0 x*x2 x1
埃特金方法 x y y = x x* y=φ(x) x1 x0 x2 x y y = x x* y=φ(x) x1 x0 x2 一般迭代过程 迭代加速过程

埃特全方法 迭代加速过程 过程分析: (1)从x出发先迭代两次,得到 Ax。,x x=p(x)乃x2=p(x) 在y=0(x)上构成两点4(x。,xbB(区,x) x,x,可以看作是临时变量 y-o(x) B(,) (2)求直线AB与y=x的交点(x,x)为 将x 作为第一次的迭代结果。 直线AB方程: x-x=无-x x=p(x)x2=p(x)》 y-x x,-x 迭代方程:x= x无2-x k+ x-2x+ x。-2元+x
埃特金方法 x y y = x x* y=φ(x) x0 x1 迭代加速过程1 x ( , ) 0 1 A x x ( , ) 1 2 B x x 过程分析:( ) ( ) (1) 1 0 2 1 0 x x x x x = , = 从 出发先迭代两次,得到 ( ) ( , ) ( , ) 0 1 1 2 在y = x 上构成两点A x x ,B x x 将 作为第一次的迭代结果。 求直线 与 的交点 , 1 1 1 (2) ( , ) x AB y = x x x x1 ,x2 可以看作是临时变量 2 1 1 0 1 0 AB x x x x y x x x − − = − − 直线 方程: 0 1 2 2 0 2 1 1 x 2x x x x x x − + − 迭代方程: = − + − = = = + 1 2 2 2 1 1 1 2 1 2 ( ) ( ) x x x x x x x x x x x k k k k ,

例1: 灭=p(x)为x2=p(区)》 用埃特金方法求方程2+x-4=0的根 x玉2一 (初值x。=1)。 x-2x+x, 解:将方程改写成达代格式X=h(4一 )取x,=1 第1次选代:正-(4-)=05493L.=号M4-05493)=0.61929 得到:x= x元2-x2 1×0.61929-0.54931 =0.60988 x。-2x+x,1-2×0.54931+0.61929 1 1 第2次迭代:元=h(4-0.60988)=0.61043,元=。ln(4-0.61043)=0.61035 2 得到:x,= x2-x 0.60988×0.61035-0.61043 =0.61036 x-2x+x0.60988-2×0.61043+0.61035 x,-x=0.61036-0.61035=0.0001 ∴.可以认为迭代过程已经收敛,将x,作为方程根的近似
− + − = = = + 1 2 2 2 1 1 1 2 1 2 ( ) ( ) x x x x x x x x x x x k k k k , 初值 。 用埃特金方法求方程 的根 例 : ( 1) 4 0 1 0 2 = + − = x e x x x = ln (4 − x) 2 1 解:将方程改写成迭代格式 ln( 4 0.54931) 0.61929 2 1 ln( 4 1) 0.54931 2 1 第1次迭代:x1 = − = ,x2 = − = 0.60988 1 2 0.54931 0.61929 1 0.61929 0.54931 2 2 0 1 2 2 0 2 1 1 = − + − = − + − = x x x x x x 得到:x 取x0 = 1 ln( 4 0.61043) 0.61035 2 1 ln( 4 0.60988) 0.61043 2 1 2 第 次迭代:x1 = − = ,x2 = − = 0.61036 0.60988 2 0.61043 0.61035 0.60988 0.61035 0.61043 2 2 1 1 2 2 1 2 1 2 = − + − = − + − = x x x x x x 得到:x 可以认为迭代过程已经收敛,将 2作为方程根的近似。 2 2 0.61036 0.61035 0.0001 x x x − = − =