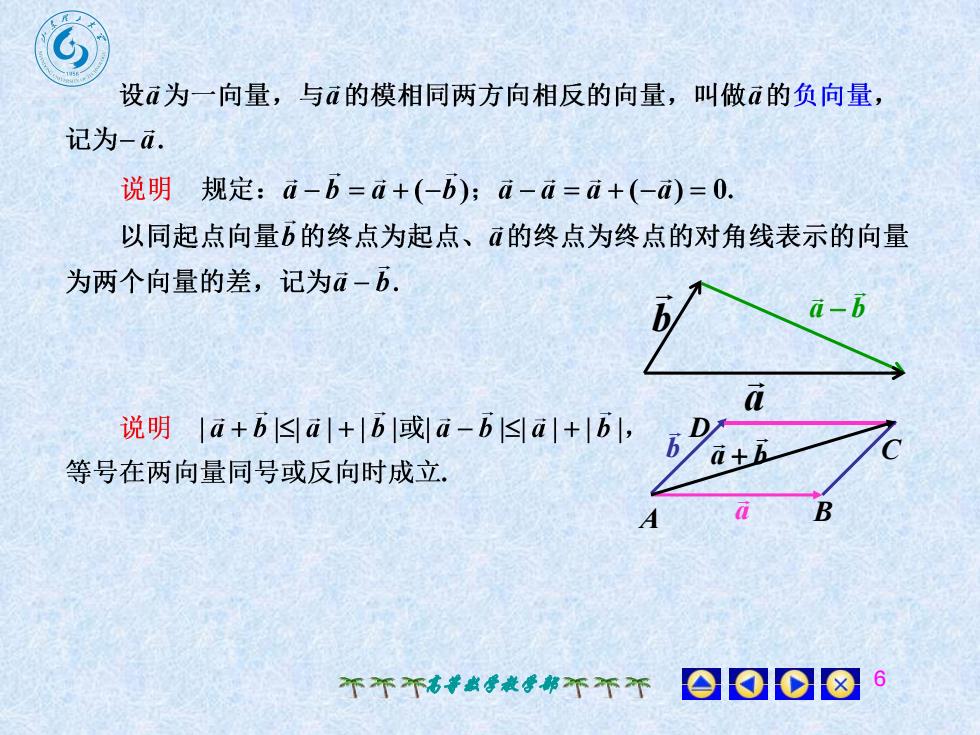
设a为一向量,与a的模相同两方向相反的向量,叫做a的负向量记为-a.说明规定: a-b=a+(-b); a-a=a+(-a)=0.以同起点向量b的终点为起点、的终点为终点的对角线表示的向量为两个向量的差,记为a一b0a说明 |a+b[<[a|+|b|或|a-b<[a|+|b],Dba+h等号在两向量同号或反向时成立BfCA0008个个个高等数学教学部
高等数学教学部 6 a b a b a b a b A B C D

2、向量与数的乘法向量的数乘(a)设为常数,与向量a的乘积规定为:(1)a--a];(2)>0时,a与a同向;<0时,a与a反向:=0时,a=0说明1a=a; (-1)a=-a运算律:(1)交换律 ·a=a·;(2)结合律(μu)a= a(ua);(3)分配律 (a+ μu)a = Ma + ua;(a+ b)= a+ ab;向量的加法及数乘运算称为向量的线性运算008个个个高数学教学部不不个
高等数学教学部 7
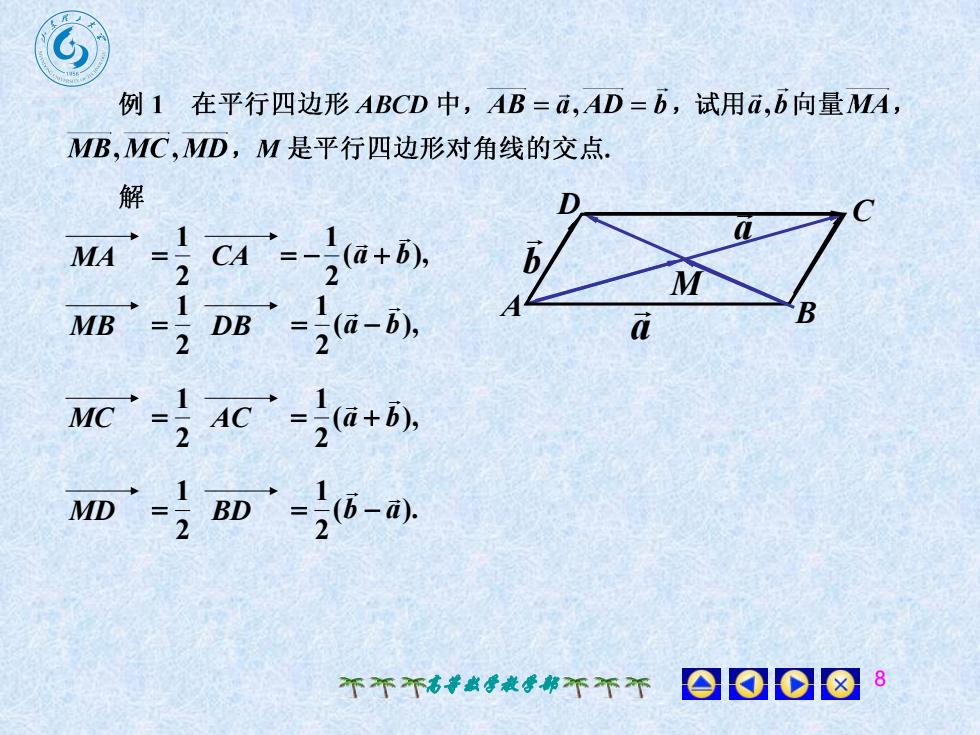
例1 在平行四边形ABCD中,AB=a,AD=b,试用a,b向量MAMB,MC,MD,M是平行四边形对角线的交点解D福aI(a+b),bMACA21MAB(a-b)DBaMB12AC -,(a+b)1-2MCBD(6-a),MD280008不不不高尊数学教学部不不个
高等数学教学部 8 MA 2 1 A B D C M a b a CA ( ), 2 1 a b MB 2 1 DB ( ), 2 1 a b MC 2 1 AC ( ), 2 1 a b MD 2 1 BD ( ). 2 1 b a

向量的单位化(b)设e,表示与非零向量a同向的单位向量,则é,a=aé定理 1设向量a≠0,则向量b //a的充分必要条件是存在唯一的实数几,使b = Λa.证充分性假定b=aa,当>0时,b与a同向;当元=0时,b=0;当几<0时,b与a反向,均有b lla.必要性假定bllab取[[b与a同向时a取正,b与a反向时几取负,可知b=aa,a16al-|b].因为b与a同向;a=aa唯一性 假定b=a,b = ua =(-u)a=0 → =μ.0008中个不高教学教学部不不不
高等数学教学部 9 ( )a 0