
2-2行列式的性质和计算、行列式的性质性质1n阶行列式按任一行展开,其值相等,即det A=a,A, +a2A,+L +amA,=a a,A(i=1,2,L ,n)推论若行列式的某行元素全为零,则行列式的值为零。60015-13- 2例1计算行列式 D=0020314- 30603-2=12解:按第二行展开D=2(-1)3+235-2=-2'64-341-3
2-2 行列式的性质和计 一、行列式的性质 算 性质1 n 阶行列式按任一行展开,其值相等,即 推论 若行列式的某行元素全为零,则行列式的值为零。 例1 计算行列式 解:按第二行展开

Lauaj2ainLa22a2n因此,可以化成上D例2计算n阶上三角行列式0L三角来求。am解:可按第n行展开Laain-1a2La22a2n-1D, =(- 1)"+=a.D..n-1 =aman-In-Dn-2 =aman-In-L an+nam0Lan-In-1 In-1=am2L amm
例2 计算 n 阶上三角行列式 解:可按第 n 行展开 因此,可以化成上 三角来求

性质2若n阶行列式的某两行元素对应相等,则行列式的值为零用数学归纳法证明:当n=2时,由对角线展开法,结论显然成立;假设当n=k(k33)时q,结论成立,即s=1,2,L,n)D,=0且令n=k+1D,按第k+1行展开,则k+=ak+1Ak+11+ak+12Ak+12+L+ak+1k+1Ak+1k+其中 Ak+11,Ak+12,L,Ak+1k+1都是k阶行列式,且第i行与第等证毕故Dk-↑ = 0由假设可知Ak+11=Ak+12=L =Ak+1k+1=0
性质2 若 n 阶行列式的某两行元素对应相等,则行列式的值为 零。 用数学归纳法证明: 当 时,由对角线展开法,结论显然成立; 假设当 时,结论成立,即 且 令 , 按第 k+1 行展开, 则 其中 都是 k 阶行列式,且第 i 行与第 j 行元素对应相 等 由假设可知 证毕,故

性质3(可加性)LLLa12aua/2ainaaj1ai2ainanLLLLLLLLLLLLb.LLbinb,2Lbinb., +Cib,z +C,2+Ci+CinCi2CinLLLLVLLLLLLLLLLanlan2anlanlan2aannan2an证明:将左端行列式按第i行展开,得D=(b, +c,)A, +(b2 +c2)A2 +L +(b.m+cm)Am=(b,A, +b,A2 +L +bmAm)+(c,A, +C2A, +L +cmAm)= D, + D,证毕
性质3 (可加性) 证明:将左端行列式按第 i 行展开,得 证毕
性质4(行列式的初等变换)(1)行列式的某{k,等于用数k乘以此行列式;行元素都乘以同一个数-LL证明:aauna.anai2ai2LLLLLLLLka,ka,2Lka..设D=则=ka,A, +ka,A, +L +ka.A,La,tai2a..LLLLLLLLLannan2a,ntL=k(a,A +a,A,+L +a.A,)=kDanan2amm推论①行列式的某-行元素的公因子可以提到行列式前面;LLaanaua2anai2LLLLLLLLka,ika,2LkainL=ka,ia;2ainLLLLLLLLLLan2asna,an2anamn
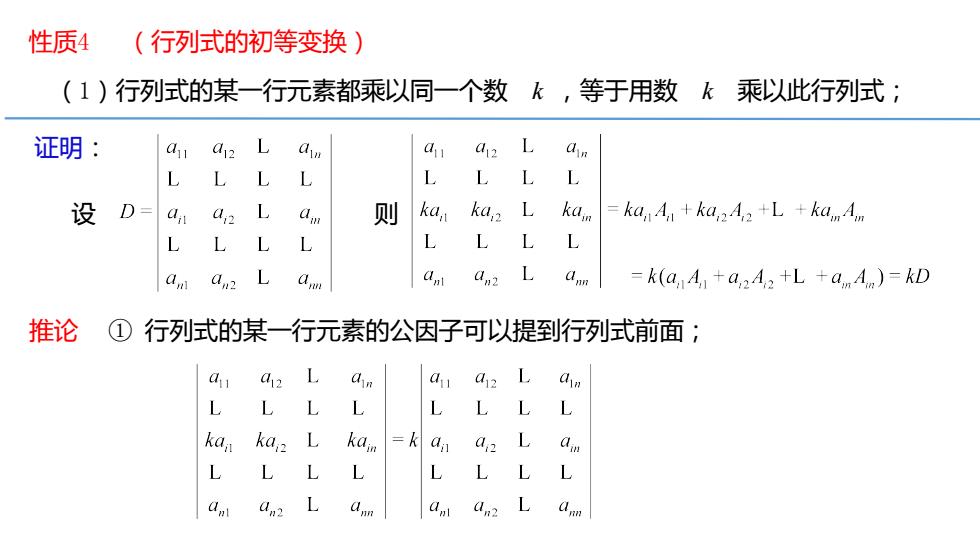
性质4 (行列式的初等变换) (1)行列式的某一行元素都乘以同一个数 k ,等于用数 k 乘以此行列式; 证明: 设 则 推论 ① 行列式的某一行元素的公因子可以提到行列式前面;