《线性代数》课程教学资源（课件讲稿，B）第一章矩阵及其初等变换_1-1矩阵及其运算2/2

第一章矩阵及其初等变换加油！

第一章 矩阵及其初等变换

3、矩阵的乘法火腿肠引例包海豆火腿肠菜带皮包海豆F皮菜带121.53(元)3171甲(10.5)21120411.510(320丙31×1+1×2+3×1.5+1×3=10.54×15+1×3=112×1+0×2-3 × 1= 10X3加油！

3、矩阵的乘法 引例 1 1 3 1 2 0 4 1 3 2 0 1           甲乙丙 12 1.53             包菜 海带 豆皮 火腿肠 包菜 海带 豆皮 火腿肠 1 2 1.5 3 （元）

矩阵的乘法1.线性变换设变量y,J2,…ym能用变量xj,Xz,,x,线性表示yi =auX, +ai2x2 +...+ainxnJ, = a2ix, +a22X, +... +a2nXn,Jm=amiXi+am2X,+...+amnXn其中系数a,(i=1,2,,m,j=1,2,…,n)为常数，这种从变量x,xz,,x,到变量yj,J2,…ym的变换叫做线性变换加油！

1 2 1 2 1 11 1 12 2 1 2 21 1 22 2 2 1 1 2 2 1 2 1 2 , , , , , , , , ( 1, 2, , , 1, 2, , ) , , , , , m n n n n n m m m mn n ij n m y y y x x x y a x a x a x y a x a x a x y a x a x a x a i m j n x x x y y y                       设变量 能用变量 线性表示， 其中系数 为常数，这种从 变量 到变量 的变换叫做线性变换. 矩阵的乘法 1.线性变换

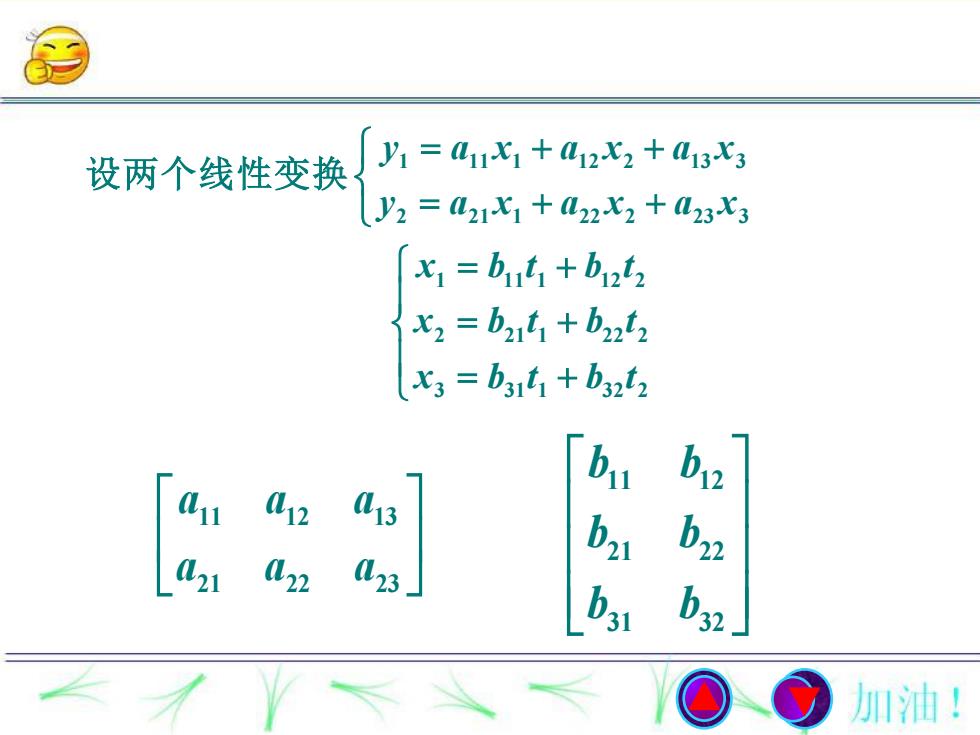
ail(121an2(2)a2n此线性变换的系数构成的m×n矩阵为aaamlm2mn称为线性变换的系数矩阵yi=aiix+ai2x+a13x设两个线性变换J2=a21X+a22X2+a23xX, = biuti + bi2tX, = b21ti + b22tXg = b3iti + b32t,加油！

11 12 1 21 22 2 1 2 . n n m m mn a a a a a a m n a a a              此线性变换的系数构成的 矩阵为 称为线性变换的系数矩阵 1 11 1 12 2 13 3 2 21 1 22 2 23 3 1 11 1 12 2 2 21 1 22 2 3 31 1 32 2 y a x a x a x y a x a x a x x b t b t x b t b t x b t b t                     设两个线性变换

V=axi+a1x+a13x设两个线性变换y2=a21+a22X2+a23x3Xi = buiti + bi2t2Xz = b21t + b22t2Xg=b3iti+b32t2ba12130D2b2a122a2321bbo31加油！

1 11 1 12 2 13 3 2 21 1 22 2 23 3 1 11 1 12 2 2 21 1 22 2 3 31 1 32 2 y a x a x a x y a x a x a x x b t b t x b t b t x b t b t                     设两个线性变换 11 12 13 21 22 23 a a a a a a       11 12 21 22 31 32 b b b b b b          