《线性代数》课程教学资源（课件讲稿，B）第二章行列式_2-4克拉默法则

第二章s4克拉默法则一、伴随矩阵可逆的充分必要条件三、克拉默法则加油！

§4 克拉默法则 第二章 二、可逆的充分必要条件 一、伴随矩阵 三、克拉默法则

引理1行列式中某一行（列）的元素与另一行（列）对应元素的代数余子式的乘积之和等于零，即,=0 (i±j)aiAj +ai2Aj2 +...+ainAin或=0(i±j)ta.oiAi-n加油！

行列式中某一行（列）的元素与另一行（列） 对应元素的代数余子式的乘积之和等于零，即 1 1 2 2 0 ( ) i j i j in jn a A a A a A i j      或 1 1 2 2 0 ( ) i j j j nj nj a A a A a A i j      引理1

143222-2-1D-1× A, +3× A,+2× A, +4× A9867—一1-25047× A +8× A12 +9× A13 +6× A.768922-21= 08976504-2加油！

11 12 13 14 1 3 2 4 2 2 1 2 =1 3 +2 +4 7 8 9 6 0 4 2 5 D A A A A          11 12 13 14 7 8 +9 +6      A A A A 7 8 9 6 2 2 1 2 7 8 9 6 0 4 2 5    =  0

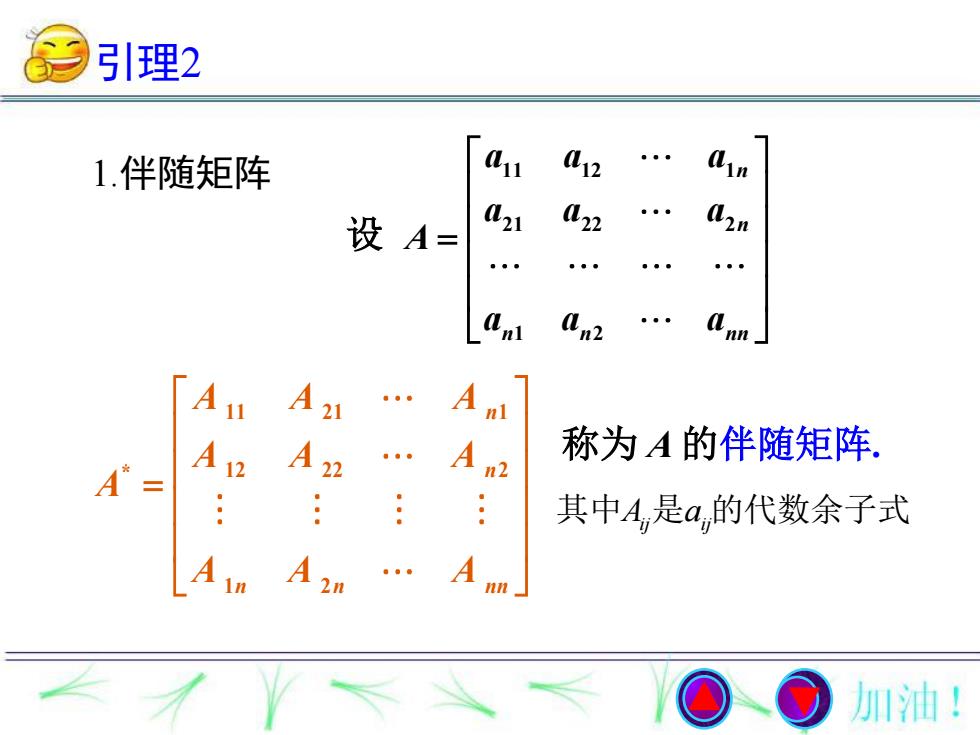
引理2al(121.伴随矩阵1(2)a222n设A:aan2anlnn称为A的伴随矩阵其中A,是a,的代数余子式2nnn加油！

11 21 1 * 12 22 2 1 2 n n n n nn A A A A A A A A A A              称为 A 的伴随矩阵. 设 11 12 1 21 22 2 1 2 n n n n nn a a a a a a A a a a              引理2 1.伴随矩阵 其中A a ij ij 是 的代数余子式

例2-110求矩阵A=-2-1的伴随矩阵013Au =1, A2 =6, A3 = -22A*=-36-3A21 = -5, A22 = -3, A23 = 1,-214A31 = -2, A32 = -3, A33 = 4加油！

1 2 1 2 0 1 0 1 3 A               求矩阵 的伴随矩阵. * 1 5 2 6 3 3 2 1 4 A                 11 12 13 21 22 23 31 32 33 1, 6, 2 5, 3, 1, 2, 3, 4 A A A A A A A A A               例