《线性代数》课程教学资源（课件讲稿，B）第四章特征值与特征向量_4-2矩阵的相似对角化

第四章S2矩阵的相似对角化一、相似矩阵的基本概念二、矩阵的相似对角化加油！

§2 矩阵的相似对角化 第四章 一、相似矩阵的基本概念 二、矩阵的相似对角化

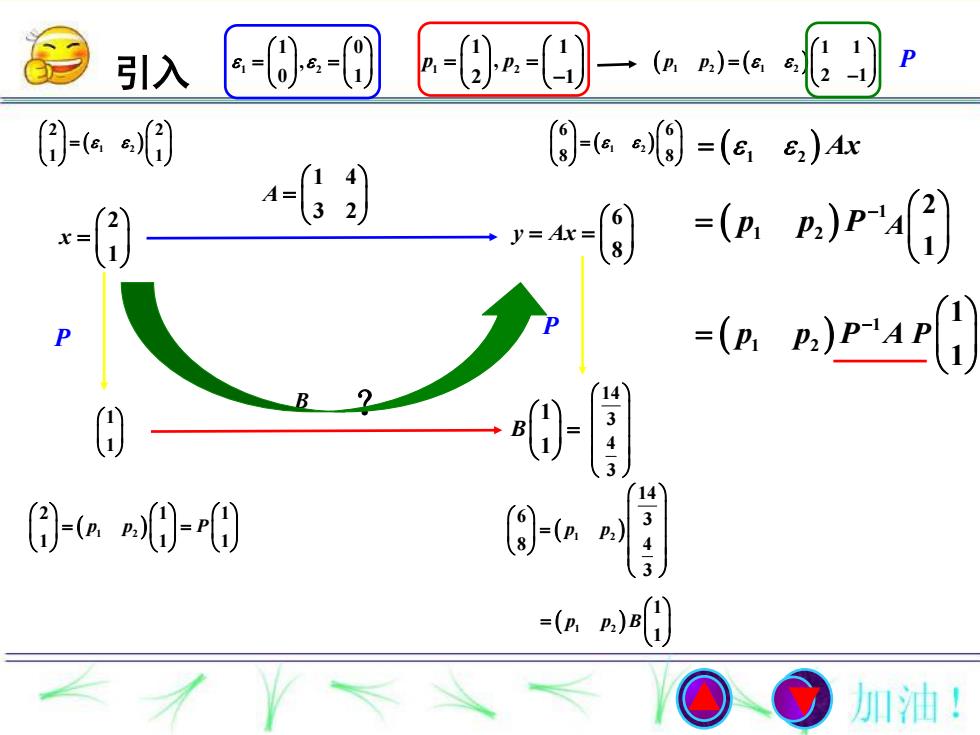
P)=(c)引入82)AxS=(p)p,)P=AxP-IAR2)C)= p(?加油！

引入 2 1 x        6 8 y Ax         1 4 3 2 A        1 2 1 0 , 0 1                 1 2 1 1 , 2 1 p p                 1 2  2 2 1 1                 1 2  6 6 8 8                   1 2  Ax  1 2  2 1 1 1 1 1 p p P                     1 1       B ？ P 14 3 4 3              1 2  14 6 3 8 4 3 p p                     1 2 1 2    1 1 2 1 p p           P P   1 1 2 p p P  2 1 A         1 1 2 p p P A  1 1 B        1 2  1 1 p p B        1 1 P      

一、相似矩阵的基本概念定义设A,B都是n阶矩阵,若有可逆矩阵P使P-1AP=B成立,则A与B相似，记为A～B(1) 反身性A~A;简单性质(2) 对称性A~B则B~A;(3)传递性A~B且B~C则A~C.加油！

1 , , , , ~ . A B n P P AP B A B A B   设 都是 阶矩阵 若有可逆矩阵 使 成立 则 与 相似，记为 定义 一、相似矩阵的基本概念 3 ~ ~ ~ .  传递性 A B B C A C 且 则 2 ~ ~  对称性 A B B A 则 ； 简单性质 1 ~ ;  反身性 A A

定理1 相似矩阵有相同的特征值证： 设A～B,则B=P-AP2I-B=2-P-IAP=p-I(aI -A) P=p-I|[2l - A|P|=[21 - A说明：特征多项式相同的矩阵不一定相似R4:0加油！

定理1 相似矩阵有相同的特征值. 1 P I A P       I A1 A B B P AP ~ ,  设 则    1 1 I B I P AP P I A P           说明：特征多项式相同的矩阵不一定相似 1 0 1 1 = = 0 1 0 1 A B             证：

例九A求Ah设矩阵A～△=证明：设A～△,则存在可逆矩阵P，使得P-1AP=Λ加油！

1 2 ~ , k n A A                  设矩阵 求 例 1 A P P AP ~ , =  证明： 设   则存在可逆矩阵 ，使得