《线性代数》课程教学资源（课件讲稿，B）第一章矩阵及其初等变换_1-3逆矩阵

第一章S3逆矩阵一、逆矩阵的定义二、逆矩阵的性质三、逆矩阵的求法加油！

§3 逆矩阵 三、逆矩阵的求法 一、逆矩阵的定义 二、逆矩阵的性质 第一章

一、引入在数的运算中，当数a≠0时，有aa-1 = a-'a= 1,其中α_为a 的倒数，（或称a的逆)在矩阵的运算中，单位阵E相当于数的乘法运算中的1那么，对于矩阵A，如果存在一个矩阵A-1,使得AA-1 = A-'A= I,则矩阵A-称为A的可逆矩阵或逆阵加油！

1 1 AA A A I,     则矩阵 称为 A 的可逆矩阵或逆阵. 1 A 1, 1 1     aa a a 在数的运算中，当数 a  0 时，有 a a 1 1  其中  为 a 的倒数，（或称 a 的逆） 在矩阵的运算中，单位阵E相当于数的乘法运算中的1， 那么，对于矩阵A，如果存在一个矩阵A -1 ,使得 一、引入

二、逆矩阵的定义定义设A是一个n阶方阵，若存在n阶方阵B，使得AB=BA=1则称A可逆的，并称B为A 的逆矩阵3-2例如B=A=25有AB=BA=I，，所以A与B互为逆阵[1 2]例如没有逆矩阵A=00加油！

定义 设A是一个n阶方阵， 若存在n阶方阵B，使得 AB = BA = I 则称 A 可逆的，并称B 为 A 的逆矩阵. 二、逆矩阵的定义 1 2 5 2 , 2 5 2 1 A B                 有AB = BA = I ，所以A 与 B 互为逆阵. 例如 1 2 0 0 A        例如 没有逆矩阵

说明：(1)若A是可逆矩阵，则A的逆矩阵是唯一的若设B和C是A的可逆矩阵，则有AB= BA=I, AC=CA=I.可得 B = IB=(CA)B=C(AB) =CI =C所以A的逆矩阵是唯一的,记作A-B=C= A-1加油！

说明: (1)若A是可逆矩阵，则A的逆矩阵是唯一的 若设B和C是A的可逆矩阵，则有 AB BA I AC CA I     , , 可得 B IB   CAB  CAB   CI C. 所以A的逆矩阵是唯一的,记作A -1 1 B C A .   

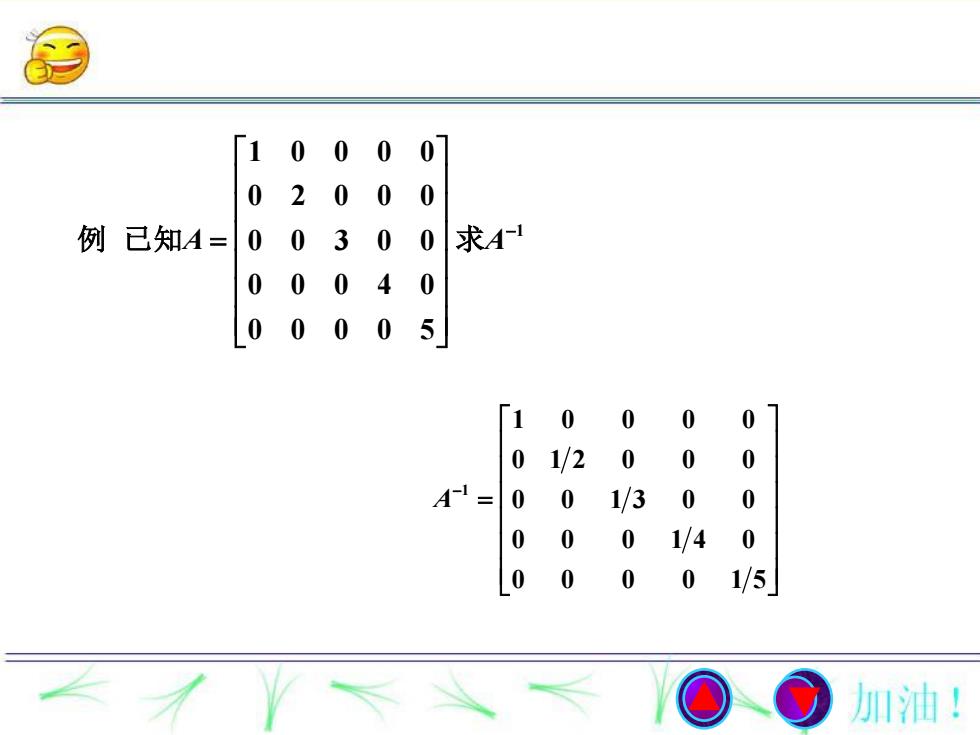
000002000求A-10300例 已知A=00000A0000500001001/20001/300000001/400001/5加油！

1 1 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 4 0 0 0 0 0 5 A A                  例 已知 求 1 1 0 0 0 0 0 1 2 0 0 0 0 0 1 3 0 0 0 0 0 1 4 0 0 0 0 0 1 5 A                  