《线性代数》课程教学资源（课件讲稿，B）第四章特征值与特征向量_4-1特征值与特征向量的概念与计算

第四章S 1 特征值与特征向量的概念与计算特征值与特征向量的定义二特征值与特征向量的性质三、特征值与特征向量的求法加油！

§1 特征值与特征向量的 概念与计算 第四章 一、 特征值与特征向量的定义 二、 特征值与特征向量的性质 三、 特征值与特征向量的求法

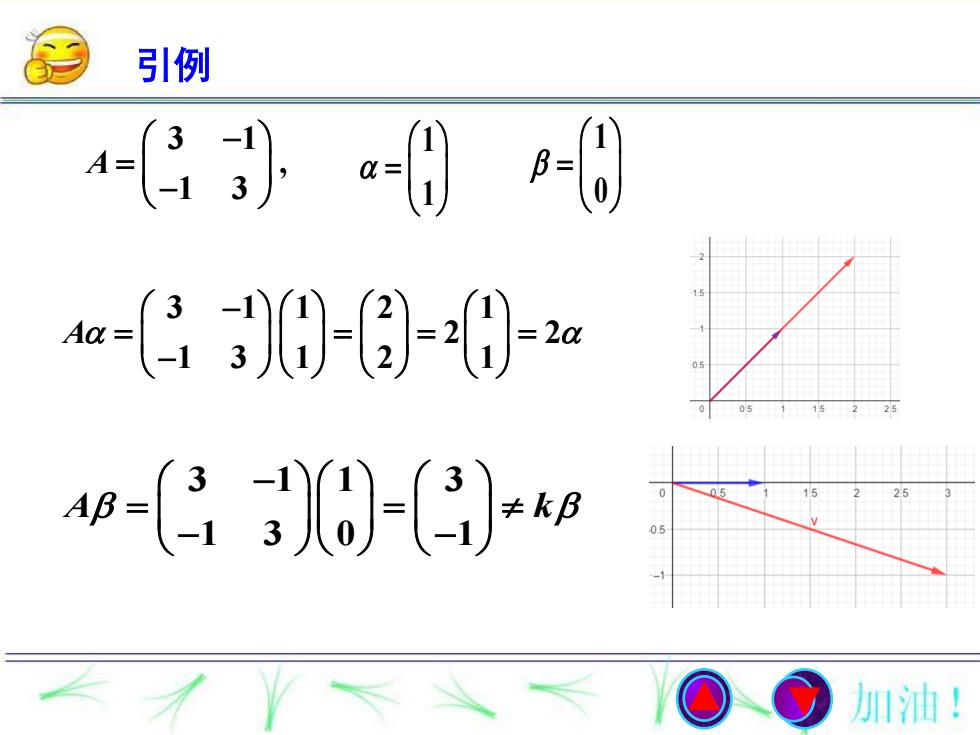
引例118α=01Aa20≠kβ0.5加油！

引例 1 1         3 1 , 1 3 A          3 1 1 2 1 2 2 1 3 1 2 1 A                                3 1 1 3 1 3 0 1 A k                           0 . 1        

一、定义设A是n阶方阵，若存在实数和非零向量α，使得Aα=aα成立，则称数2为方阵A的特征值非零向量α称为A的对应于特征值的特征向量加油！

, . A n A AA         设 是 阶 方 阵,若 存 在 实 数 和 非 零 向 量 使 得 成 立， 则称数 为方阵 的 非零向量 称为 的对特征值 应于特征值 的 ， 特 征 向 量 一、 定义

二、性质1. 设 Aα = α (α ± 0),则(k+0)A (kα)=k(Aα)=k(αα)=(kα)2.设Aα, = α, (i= 1,2,.,s),则A(k,a, + k,a, +...+ k,a,)= k,Aα, + k,Aα, +..+ k,Aa=a(ka,+k,α, +.+k,α,)说明：一个特征值可以有多个特征向量一个特征向量只能属于一个特征值加油！

2. 1, 2, , ,   A i s   i i 设   则 说明：一个特征值可以有多个特征向量           1. 0 , A A k k A k k                设 则 二、 性质 （k≠0） 一个特征向量只能属于一个特征值 1 1 2 2 s s A k k k  1 1 2 2       s s      k A k A k A      1 1 2 2 . s s         k k k

特征子空间设=α|Aα=α,αR"故V,是n维向量空间R"的子空间·V,称为矩阵 A的特征子空间.则由特征值与特征向量的性质可知：Vα,βeVa, α+βeV,VαeV,keR, kαeV,.加油！

特征子空间  | , R  n V A  设         , , , R , . V V V k k V                   则由特征值与特征向量的性质可知： R . . n V n V A   故 是 维 向 量 空 间 的 子 空 间 称 为 矩 阵 的 特 征 子 空 间