
第二节微积分基本公式问题的提出二、积分上限函数及其导数三、牛顿一菜布尼茨公式四、小结
第二节 微积分基本公式 • 一、问题的提出 • 二、积分上限函数及其导数 • 三、牛顿—莱布尼茨公式 • 四、小结

问题的提出一、变速直线运动中位置函数与速度函数的关系设某物体作直线运动,已知速度v=v(t)是[T,T,]上的一个连续函数,且v(t)≥ 0,s= s(t)是位置函数,求物体在这段时间内所经过的路程v(t)dt变速直线运动中路程为另一方面这段路程可表示为 s(T)一S(T)v(t)dt = s(T,)-s(T). 其中 s'(t)= v(t)一般的,设f(x)在[a,b]连续,且 F'(x)=f(x).J' f(x)dx?F(b) -F(a)
变速直线运动中位置函数与速度函数的关系 变速直线运动中路程为 2 1 ( ) T T v t dt 另一方面这段路程可表示为 ( ) ( ) 2 T1 s T − s F x f x ( ) ( ). = ( ) ( ) ( ). 2 1 2 1 v t dt s T s T T T = − 其中 s(t) = v(t). 一般的,设f(x)在[a,b]连续,且 ( ) ( ) ( ). b a f x dx F b F a = − 一、问题的提出 1 2 ( ) [ , ] ( ) 0 ( ) v v t T T t v t s s t = = 设某物体作直线运动,已知速度 是 上 的一个连续函数,且 , 是位置函 数,求物体在这段时间内所经过的路程

二、积分上限函数及其导数设函数f(x)在区间[a,b]上连续,并且设x为[a,b]上的一点,在区间[a,x]考察定积分J f(x)dx= J" f(t)dt如果上限x在区间[a,b]上任意变动,则对于每一个取定的x值,定积分有一个对应值,所以它在[a,b]定义了一个函数记@(x)=[ f(t)dt.积分上限函数
x a f (x)dx = x a f (t)dt ( ) ( ) . x a x f t dt = 记 积分上限函数 二、积分上限函数及其导数 ( ) [ , ] [ , ] [ , ] f x a b x a b a x 设函数 在区间 上连续,并且设 为 上的一点,在区间 考察定积分 [ , ] [ , ] x a b x a b 如果上限 在区间 上任意变动,则 对于每一个取定的 值,定积分有一个对 应值,所以它在 定义了一个函数
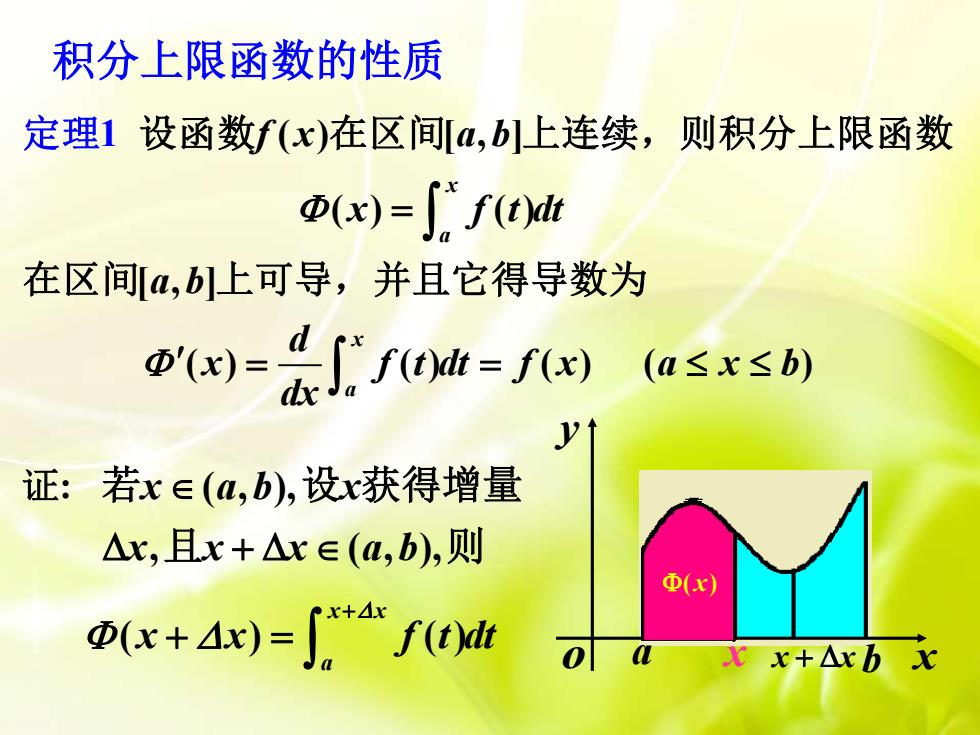
积分上限函数的性质定理1设函数f(x)在区间[a,b]上连续,则积分上限函数Φ(x)= f f(t)dt在区间[a,b]上可导,并且它得导数为d@'(x) =f(t)dt = f(x)(a≤x≤b)dx2yt证:若xE(a,b),设x获得增量Ax,且x + Ar E (a,b),则@(x)x+4x@(x+ 4x) = [x+4f(t)dtolaxx+Axbx
a b x yo 积分上限函数的性质 x + x 证: ( ) ( ) x x a x x f t dt + + = (x) x ( , ), , ( , ), x a b x x x x a b + 若 设 获得增量 且 则 ( ) [ , ] ( ) ( ) [ , ] ( ) ( ) ( ) ) 1 ( x a x a f x a b x f t dt a b d x f t dt f x a x b dx = = = 设函数 在区间 上连续,则积分上限函数 在区间 上可导,并且它 为 定 得导数 理

AΦ = Φ(x + 4x)-Φ(x)x+4x-J*+" f(t)dt - f" f(t)dt+A= " f(t)dt + J+*" f(t)dt - J f(t)dtx+4xf(t)dt由积分中值定理得4@ = f()4x介于x与x+△x之间△@4Φlim=lim f(5)= f(5),4x△x4x→04x-→0Ax0,5→x.. @Φ'(x)= f(x)
f t dt f t dt f t dt x a x x x x a = + − + ( ) ( ) ( ) ( ) x x x f t dt + = 由积分中值定理得 = f x ( ) ξ介于x x x 与 + 之间, x → 0, → x f ( ), x = 0 0 lim lim ( ) x x f x → → = = ( ) ( ). x f x = + − ( ) ( ) x x x f t dt f t dt x a x x a = − + ( ) ( )