《线性代数》课程教学资源（课件讲稿，B）第一章矩阵及其初等变换_1-2高斯消元法与矩阵的初等变换

第一章S2高斯消元法与矩阵的初等变换一、高斯消元法二、矩阵的初等变换三、初等矩阵加油！

§2 高斯消元法与矩阵的初等变换 三、初等矩阵 一、高斯消元法 二、矩阵的初等变换 第一章

n元线性方程组axi +ai2x, +..+ainx, =baux, +aix, +... +ainx, = 0a21X, +a2x, +.. +a2nxn =b,a21Xi +a22X2 +...+a2nx, =0=b+amx,+...+amx.=0+amx.amX +am2X, +.a.X-mm12220baxa12Ah(21a221a2nX2L.b.0am2Xnaamlmn齐次方程组 Ax = 0非齐次方程组 Ax= b加油！

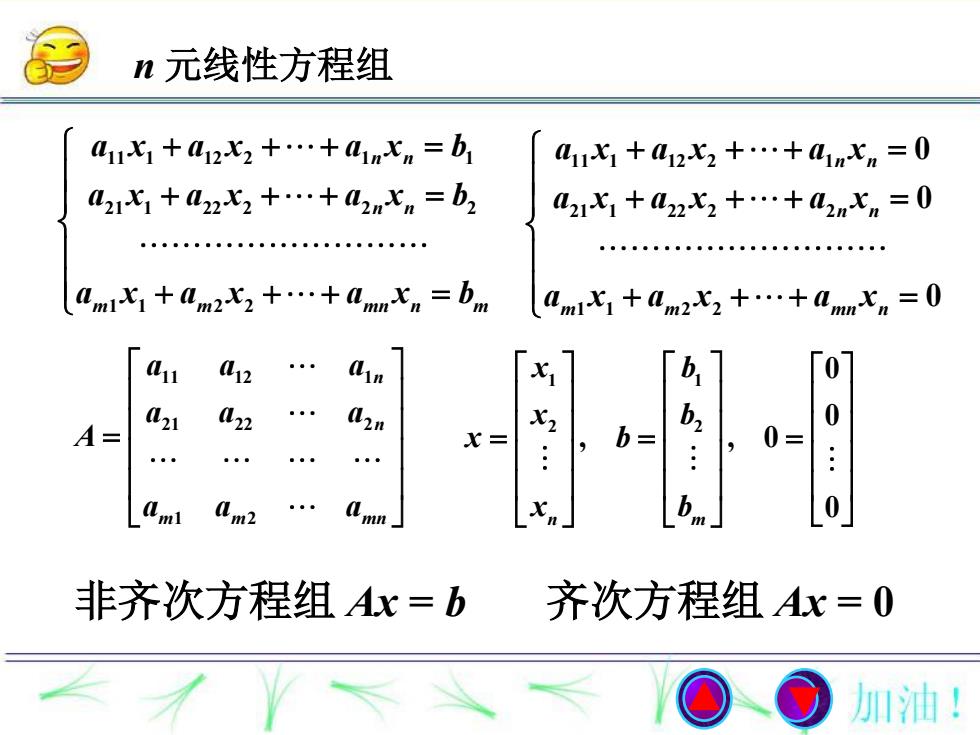
n 元线性方程组 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b                    11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a              1 1 2 2 0 0 , , 0 n m 0 x b x b x b x b                                        非齐次方程组 Ax = b 齐次方程组 Ax = 0 11 1 12 2 1 21 1 22 2 2 1 1 2 2 0 0 0 n n n n m m mn n a x a x a x a x a x a x a x a x a x                   

一、高斯消元法今有雉兔同笼，上有三十五头，下有九十四足问雉兔各几何？设鸡有x1只，兔子有x2只35X +x, = 3594M2x, + 4x, = 94加油！

今有雉兔同笼，上有三十五头，下有九十四足， 问雉兔各几何？ 1 2 1 2 35 2 4 94 x x x x        1 1 35 2 4 94       一、高斯消元法

35X +x, = 352:942x +4x, = 941351X +x = 35-2①+②02 242x, = 241 351x + x, = 35一0112x, =12/ 23)= 23-1×②+①x12!0X, = 12加油！

1 2 1 2 35 2 4 94 x x x x        1 1 35 2 4 94       1 2 2 35 2 24 x x x       1 1 35 0 2 24       1 2 2 35 12 x x x       1 2 23 12 x x      1 1 35 0 1 12       1 0 23 0 1 12       -2 1 + 2 2 1 2  1 2 + 1

-2 :1233x -2x2 =12,3-263xi - 2x2 = 6.-2 1 12 33x - 2x2 =12,-1@+②0= -6.加油！

1 2 1 2 3 2 12, 3 2 6. x x x x        3 2 12 3 2 6         3 2 12 0 0 6         3 2 12, 1 2 0 6.  x x       -1 1 + 2