《线性代数》课程教学资源（课件讲稿，B）第二章行列式_2-5矩阵的秩

第二章s5矩阵的秩一、矩阵秩的概念二、矩阵秩的计算三、矩阵秩的性质加油！

§5 矩阵的秩 第二章 一、矩阵秩的概念 二、矩阵秩的计算 三、矩阵秩的性质

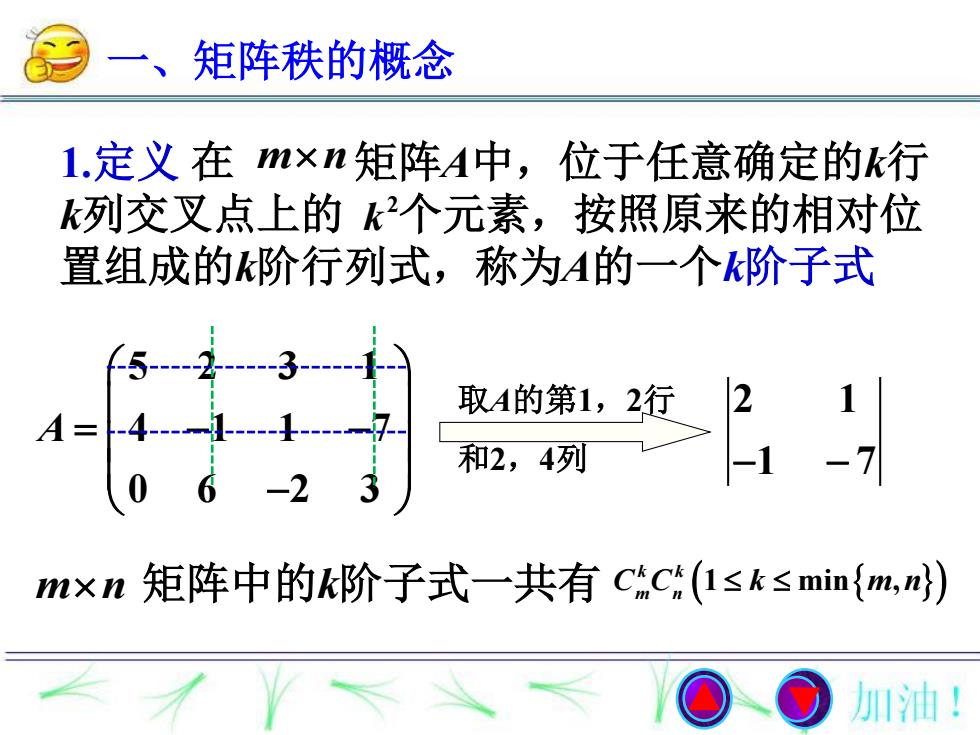
一、矩阵秩的概念1.定义在 mxn矩阵A中，位于任意确定的k行k列交又点上的k2个元素，按照原来的相对位置组成的阶行列式，称为A的一个k阶子式2取A的第1，2行4和2，4列mxn 矩阵中的k阶子式一共有 Chc(1≤k≤minm,n)加油！

一、矩阵秩的概念 5 2 3 1 4 1 1 7 0 6 2 3 A               取A的第1，2行 和2，4列 2 1   1 7 1.定义 在 矩阵A中，位于任意确定的k行 k列交叉点上的 个元素，按照原来的相对位 置组成的k阶行列式，称为A的一个k阶子式 m n 2 k m n 矩阵中的k阶子式一共有 1 min ,   k k C C k m n m n  

2.矩阵A的秩矩阵中不为零的子式的最高阶数，记为R(A).说明：矩阵A的秩等于r存在不为零的阶子式同时所有的r+1阶子式全部为零加油！

2.矩阵A的秩 矩阵中不为零的子式的最高阶数，记为R(A).    同时所有的  阶子式全部为零 存在不为零的 阶子式 r 1 r 矩阵A的秩等于r  说明：

例求矩阵的秩R(A)=110222R(B)=2(2) B =22C中所有3阶子式全为零，2824(3) C =可得 R(C)= 2.3062加油！

1 1 (1) ; 2 2 248 (2) ; 1 2 1 1 2 4 1 (3) 2 4 8 2 3 6 2 0 A B C                        例 求矩阵的秩 3 ( ) 2. 中所有 阶子式全为零， 可得 C R C  R(A)=1 R(B)=2

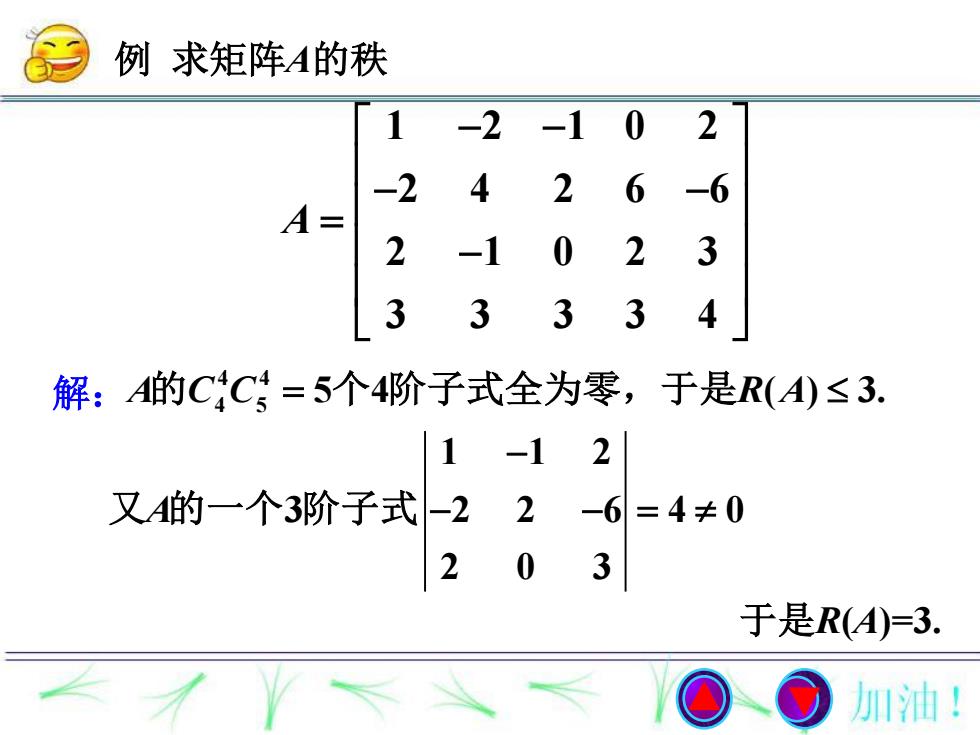
例求矩阵A的秩02-2-11264-6-2A=2032-133334解：A的C4C=5个4阶子式全为零，于是R(A)≤3.21-1 2-6又A的一个3阶子式-2=4±0023于是R(A)=3.加油！

例 求矩阵A的秩 4 4 4 5 A C C R A 的   5 4 ( ) 3. 个 阶子式全为零，于是 于是R(A)=3. 解： 1 2 1 0 2 2 4 2 6 6 2 1 0 2 3 3 3 3 3 4 A                   1 1 2 3 2 2 6 4 0 2 0 3 A  又 的一个 阶子式    