《线性代数》课程教学资源（课件讲稿，B）第一章矩阵及其初等变换_1-1矩阵及其运算2/2

yi =(aubu + a12b21 + a13b31)t, + (au,b12 + a2b22 +a13b32)ty2 =(a21b1+a22b2 + a23b31)t +(a2bi2 + a22b22 +a23b32)t,abu+arba +aibaub12+a.b22+a.baz,b12 + a2b22 +a23b3a21bi1 +a22b21 +a23b加油！

1 11 11 12 21 13 31 1 11 12 12 22 13 32 2 2 21 11 22 21 23 31 1 21 12 22 22 23 32 2 ( ) ( ) ( ) ( ) y a b a b a b t a b a b a b t y a b a b a b t a b a b a b t                11 11 12 21 13 31 11 12 12 22 13 32 21 11 22 21 23 31 21 12 22 22 23 32 a b a b a b a b a b a b a b a b a b a b a b a b               11 12 13 21 22 23 a a a a a a       11 12 21 22 31 32 b b b b b b           =

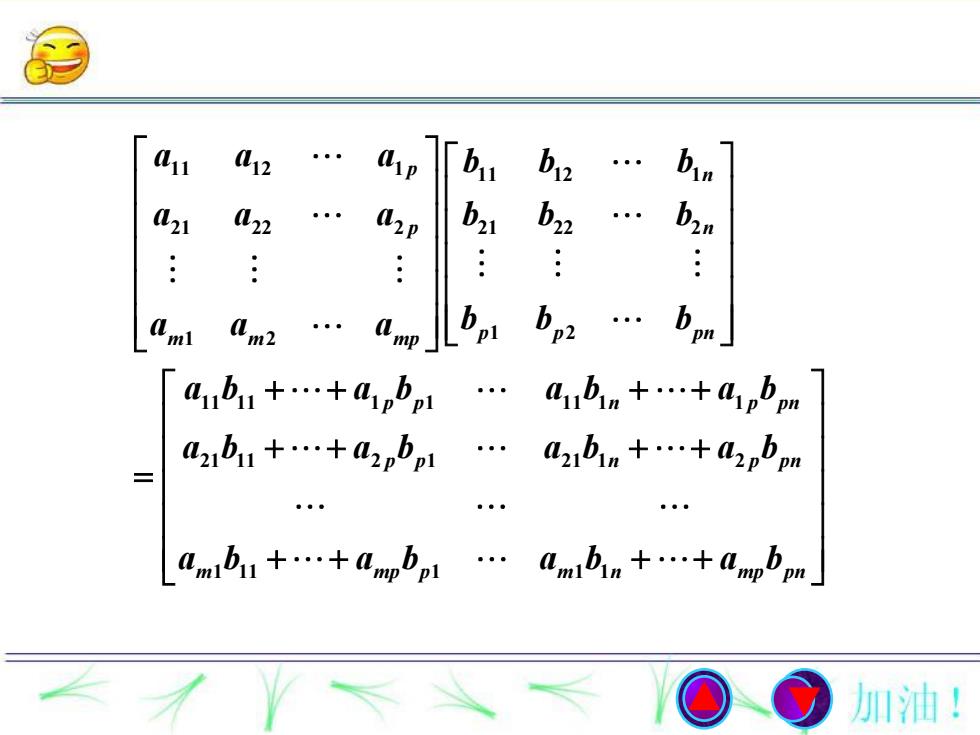
定义4设A=(a)是一个m×p矩阵,B=(b.)是一个p×n矩阵作m×n矩阵C=(c,)，其中C, = ab, +anba, +.+agb -2aikbkjk=1矩阵C称为矩阵A与矩阵B的乘积，记作C=AB加油！

1 1 2 2 1 ( ) , ( ) , ( ) ij ij ij p ij i j i j ip pj ik kj k A a m p B b p n m n C c c a b a b a b a b C A B C AB               设 是一个 矩阵 是一个 矩阵 作 矩阵 ，其中 ， 矩阵 称为矩阵 与矩阵 的乘积，记作 定义4

anl2baabr21Tb2b(n)(22anp2n..bbbaaapp2pnm2mlmpa,bu+a0a.bDIpn2a2tbu +..+a2pbpl+..+a..baz,bin0pnbambu +..+a....h+..+a..a..0mimpnDmppn加油！

11 12 1 11 12 1 21 22 2 21 22 2 1 2 1 2 11 11 1 1 11 1 1 21 11 2 1 21 1 2 1 11 1 1 1 p n p n m m mp p p pn p p n p pn p p n p pn m mp p m n mp pn a a a b b b a a a b b b a a a b b b a b a b a b a b a b a b a b a b a b a b a b a b                                                       

210221例设A=01-13求ABB =030241解：1×2+0×1+2×3-1×41×1+0×2+2×0-1×1AB =0×1+1×2-1×0+3×10×2+1×1-1x3+3×4-1×1+2×2+0×0+1×1 -1×2+2×1+0×3+1×4041054加油！

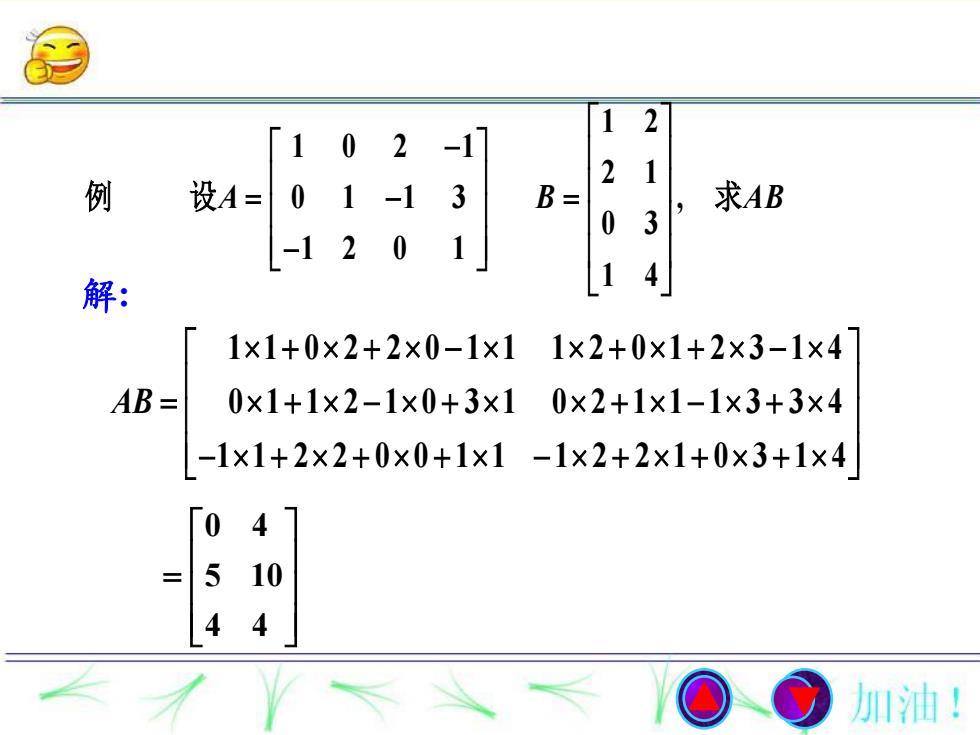
1 2 1 0 2 1 2 1 0 1 1 3 , 0 3 1 2 0 1 1 4 A B AB                            例 设 求 解: 1 1 0 2 2 0 1 1 1 2 0 1 2 3 1 4 0 1 1 2 1 0 3 1 0 2 1 1 1 3 3 4 1 1 2 2 0 0 1 1 1 2 2 1 0 3 1 4 AB                                                        0 4 5 10 4 4           

乘法性质：设下列矩阵都可以进行有关运算1. A(BC) = (AB)C2. k(AB)=(kA)B = A(kB)(k是数)3. A(B+C)= AB+AC(B + C)A = BA + CA加油！

乘法性质：设下列矩阵都可以进行有关运算 3. ( ) ( ) A B C AB AC B C A BA CA       2 . ( ) ( ) ( ) ( ) k A B k A B A k B k   是 数 1. ( ) ( ) A BC AB C 