
77第1章1-1将序列x[K]-(1-1012;k=0,1,2,3,4]表示为u[K]及u[K]延迟的和。解: x [k]=(u[K] - u[k-1D - (u[k-1] - u[k-2]) +(u[k-3] -u[k-4])+2(u[k-4] - u[k-5])=u[K] -2u[k-1] + u[k-2] +u[k-3] + u[k-4] -2 u[k-5]1-2判断下列系统是否为(1)线性(2)因果(3)时不变(4)稳定(1)[k]=k"x[K] (2)y[K]=x [K] (3)y[K]=a+2x[k-1]a=o(4) k]=a+ xk-1 a0 (5)[k]=a[-kl a*01=0解:(1)T(ax,[k]+bx, [k] = k’ (ax [k]+ bx,[kD)= k’ax [k]+k'bx,[k]= aT(x [k]) +bT(x,[k])所以系统线性k时刻的输出只和k时刻的输入有关,系统因果。系统时变T(x[k-n])=k’x[k -n]+y[k-n]=(k-n)"x[k-n]当输入有界时输出可以是无界的,所以系统是不稳定的。(2)非线性、因果、时不变、稳定T(bx,[k]+cx, [k]]=a+Z--- (bx,[k -]]+ cx,[k-]])(3)=a+Z-- bx,[k-1]+a+Ei--s cx,[k-1]- a = by,[K]+cy,[Kk]- a所以系统非线性k时刻的输出和k+1,k+2,.,k+5时刻的输入有关,系统非因果。 x[k-n-1=[k-n] T(x[k-n)=a+)系统非时变(=-s当|x[k]≤M,<0时[y[k]≤|a| +--x[k -1]≤[a| +11M所以当α是有限时系统稳定。(4)非线性、因果、时不变、稳定(5)线性、非因果、时变、稳定1-3设确定下列系统是否为线性、时不变系统。(1)[k]= 2 x[n8[k-nM](2) [K]=x[K] 8[k-nM]其中M为正整数。解:
77 第 1 章 1-1 将序列 x [k]={1 –1 0 1 2; k=0,1,2,3,4}表示为 u[k]及 u[k]延迟的和。 解:x [k]=(u[k] - u[k-1]) – (u[k-1] - u[k-2]) +(u[k-3] - u[k-4])+2(u[k-4] - u[k-5]) =u[k] -2u[k-1] + u[k-2] +u[k-3] + u[k-4] -2 u[k-5] 1-2 判断下列系统是否为 (1)线性 (2)因果 (3)时不变 (4)稳定 (1) [ ] [ ] 2 y k = k x k (2) [ ] [ ] 3 y k = x k (3) [ ] [ ] 5 5 y k a x k l l = + å - =- a ¹ 0 (4) [ ] [ ] 5 0 y k a x k l l = +å - = a ¹ 0 (5) y[k ] = ax[-k ] a ¹ 0 解:(1) { [ ] [ ]} ( [ ] [ ]) [ ] [ ] { [ ]} { [ ]} 2 1 2 2 1 2 1 2 2 1 2 T ax k + bx k = k ax k + bx k = k ax k + k bx k = aT x k + bT x k 所以系统线性 k 时刻的输出只和 k 时刻的输入有关,系统因果。 { [ ]} [ ] [ ] ( ) [ ] 2 2 T x k - n = k x k - n ¹ y k - n = k - n x k - n 系统时变 当输入有界时输出可以是无界的,所以系统是不稳定的。 (2)非线性、因果、时不变、稳定 (3) { [ ] [ ]} { [ ] [ ]} 1 2 5 1 2 5 T bx k cx k a bx k l cx k l l + = + å - + - =- a bx k l a cx k l a l l = + å - + + å - - =- =- [ ] [ ] 2 5 1 5 5 5 = by1 [k] + cy2 [k] - a 所以系统非线性 k 时刻的输出和 k+1,k+2,. , k+5 时刻的输入有关,系统非因果。 { [ ]} [ ] [ ] 5 5 T x k n a x k n l y k n l - = + å - - = - =- 系统非时变 当 x[k ] £ M x < ¥时 l M x y[k ] a x[k l] a 11 5 5 £ + å - £ + =- 所以当a 是有限时,系统稳定。 (4) 非线性、因果、 时不变、稳定 (5) 线性、 非因果、时变、 稳定 1-3 设确定下列系统是否为线性、时不变系统。 (1) y[k] x[n] [k nM ] n = å - ¥ =-¥ d (2) y[k] x[k] [k nM ] n = å - ¥ =-¥ d 其中 M 为正整数。 解:

78第1章离散信号与系统分析基础T(ax,[k]+ bx,[k]) = Z (ax,[n] +bx,[n])[k - nM](1)=a 2 x,[n][k - nM]+b Z x,[n][k -nM] =aT(x,[k]) +bT(x,[k])所以系统线性。由于T(x[k-m])= 2 x[n-m]o[k-nM]= 2 x[n][k-(n+m)M][k-m]= 2 x[n]8[K-m-nM]在M±1时,T(x[k-m])±y[k-m],所以系统时变。T(ax, [k]+ bx,[k]) =(ax, [k]+ bx,[k]) 2 8[k - nM](2)=ax,[K] Z [k - nM]+ bx,[K]Z [k - nM] =aT(x,[k])+bT(x,[K]]所以系统线性。例如在M-2时输入为x[Kk]={1,2,3,4,5,6,7,.时,输出为[{1,0,30,5,0,7,)输入为x[K]x[k-1]{0,1,2,3,4,5,6,7,时输出为y[K]-{0,0,2,0,4,0,6,…由于[k-1]*y,[k],所以系统时变。1-4确定下列序列的周期(1)x,[k|= cos(0.2pk)(2)x,[k]=2 cos(0.1pk)+2sin(0.2pk)(3)x,[k]=3sin(0.8pk)-4cos(0.1pk)(4)x[k]=5sin(0.1pk)+4sin(0.9pk)-4cos(0.18pk)0.2元层1解:(1)序列的周期L=102元100.1元—1(2)L=LCM(10,20)=20LCM表示最小公倍数(Leastcommonmultiple)2元200.8元_2(3)L = LCM(5,20) = 202元5990.18元0.9元(4)L=LCM(20,20,100)=1002元1002元20
78 第 1 章 离散信号与系统分析基础 (1) { [ ] [ ]} ( [ ] [ ]) [ ] 1 2 1 2 T ax k bx k ax n bx n k nM n + = å + - ¥ =-¥ d [ ] [ ] [ ] [ ] 1 2 a x n k nM b x n k nM n n = å - + å - ¥ =-¥ ¥ =-¥ d d { [ ]} { [ ]} 1 2 = aT x k + bT x k 所以系统线性。 由于 T{x[k m]} x[n m] [k nM ] n - = å - - ¥ =-¥ d x[n] [k (n m)M ] n = å - + ¥ =-¥ d y[k m] x[n] [k m nM ] n - = å - - ¥ =-¥ d 在 M ¹1时,T{x[k - m]} ¹ y[k - m],所以系统时变。 (2) { [ ] [ ]} ( [ ] [ ]) [ ] 1 2 1 2 T ax k bx k ax k bx k k nM n + = + å - ¥ =-¥ d [ ] [ ] [ ] [ ] 1 2 ax k k nM bx k k nM n n = å - + å - ¥ =-¥ ¥ =-¥ d d { [ ]} { [ ]} 1 2 = aT x k + bT x k 所以系统线性。 例如在 M=2 时 输入为 x[k]={1,2,3,4,5,6,7,¼ }时, 输出为 y[k]={1,0,3,0,5,0,7,¼ } 输入为 x1 [k]= x[k-1]={0,1,2,3,4,5,6,7,¼ }时 输出为 y1 [k]={0,0,2,0,4,0,6,¼ } 由于 [ 1] [ ] 1 y k - ¹ y k ,所以系统时变。 1-4 确定下列序列的周期 (1) [ ] cos(0.2p ) 1 x k = k (2) [ ] 2cos(0.1p ) 2sin(0.2p ) 2 x k = k + k (3) [ ] 3sin(0.8p ) 4cos(0.1p ) 3 x k = k - k (4) [ ] 5sin(0.1p ) 4sin(0.9p ) 4cos(0.18p ) 4 x k = k + k - k 解:(1) 10 1 2 0.2 = p p 序列的周期 L =10 (2) 20 1 2 0.1 = p p L = LCM(10,20) = 20 LCM 表示最小公倍数(Least common multiple) (3) 5 2 2 0.8 = p p L = LCM(5,20) = 20 (4) 20 9 2 0.9 = p p ; 100 9 2 0.18 = p p L = LCM(20,20,100) =100

791-6已知LTI系统的单位阶跃响应为s[k],求该系统对任意输入x[K]的响应。解:由于 s[K]-T(u[K],h[K]-T(u[K]-u[k-1]=s[k]-s[k-1],所以对任意输入xk]的响应[K]为y[k]= h[K]* x[K]=(s[K]- s[k-1] *x[k]1-8设x[k]是一N点序列[10≤k≤N/2-1x[k]=3-1N/2≤k≤N-1[o其他试确定x[k]*x[k1的最大的正值和最小负值及它们的位置。解:由图可知,最大的正值位置:k1=N/2-1,k2=3N/2-1,y[k1]-y[k2]=N/2最大的负值位置:k3=N-1,J[N-1]--Nx[n]x[n] x[N /2 -1=n][N-1-n]x[3N /2-1-m]-(N /2 1)N/2=1=(N -1)0N-13N/2-11-9计算卷积[k]=x[k]*g[k][k+10≤k≤3(1)x[k]=αu[k],g[k]=β"u[k](2) x[K] = g[K] =其它10解:k<00α"βk-n=(βk+I-α*+I)/(β-α)(1)y[k]=3k≥0,α±βα"αk-"=(k+1)α*k≥0,α=β(2)x[k)=(1,2,3,4)[k)=(1,4,10,20,25,24,16)
79 1-6 已知 LTI 系统的单位阶跃响应为 s[k], 求该系统对任意输入 x[k]的响应。 解:由于 s[k]=T{u[k]},h[k]=T{u[k]- u[k-1]}= s[k]- s[k-1], 所以对任意输入 xk]的响应 y[k] 为 y[k]= h[k]* x[k]=(s[k]- s[k-1]) *x[k] 1-8 设 x[k]是一 N 点序列 ï î ï í ì - £ £ - £ £ - = 0 其他 1 / 2 1 1 0 / 2 1 [ ] N k N k N x k 试确定 x[k]* x[k]的最大的正值和最小负值及它们的位置。 解:由图可知,最大的正值位置:k1=N/2-1, k2=3N/2-1, y[k1]=y[k2]=N/2 最大的负值位置:k3=N-1, y[N-1]=-N x[n] n n n n n x[-n] - (N - 1) x[N / 2 - 1 - n] - (N / 2 - 1) x[N - 1 - n] x[3N / 2 - 1 - n] 0 N / 2 - 1 N - 1 3N / 2 - 1 1-9 计算卷积 y[k] = x[k]* g[k] (1) x[k] u[k] k = a , g[k] u[k] k = b (2) î í ì + £ £ = = 0 其它 1 0 3 [ ] [ ] k k x k g k 解: (1) ï ï ï î ï ï ï í ì = + ³ = = - - ³ ¹ < = - = - + + = å å a a a a b a b b a b a a b ( 1) 0, ( )/( ) 0, 0 0 [ ] 0 1 1 0 k k k k y k n k n k k n n k n k k k n (2)x[k]={1, 2, 3, 4} y[k]={1, 4, 10, 20, 25, 24, 16}

80第1章离散信号与系统分析基础1-12x[K],x[K]分别表示一偶对称和一奇对称序列,试判断下列序列的对称性(1)x[k]*x[K] (2) x[k]*x.[K] (3)x.[k]*x.[k]解:(1)y,[k]=x,[K]*x[k], y,[-k]=Z xe,[n]x[-k-n]=Z x,[n]x,[k+n]=x[-n]x[k-n]=Zx[n]x[K-n]=y,[K]故序列偶对称(2)y,[k]=x,[k]*x.[k], y,[-k]= x,[n]x.[--n]= x,[n]x[k+n]=Zx。[-n]x[k-n]=-Z x.[n]x.[k-n]=-y,[k]故序列奇对称(3y,[k]=xol[k]*x,[K], y,[-k]=Z x。.[n]x2[-k-n] =-Z x[n]x,[k+n]=x[-n]x[k+n]=Zx。[n]x.[k-n]=y,[k]故序列偶对称1-13试确定下列周期为4的序列的DFS系数。h[k]= (0, 1, 0, -1; k = 0,1,2,3)x[k|=(12.0,2k=0123),解: X[m]=Zx[kjWmk=[5, 1, -3, 1; m=0,1,2,3]k=0H[m]= h[kJWmk =[0, -2]. 0, 2]; m=0,1,2,3]k=01-14试确定下列周期为4的序列的周期卷积[k]=x[k]h[K]h[K]= [2,0, 1, 0; k =0,1,2,3][k]= (0, 1, 0, 2, k = 0,1,2,3] ,解:[[0]]20100[1]0042-->[2]10200[[3]51-15试确定下列周期序列的周期及DFS系数(1)x[k]= sin(pk / 4)(2)x,[k]=2sin(pk/4)+cos(pk/3)解:(1)(元/4)/2元=1/8;N=8x, [k]=-0.5j(exp(j2pk /8)-exp(-j2pk /8))=-0.5j(exp(j2pk/8)-exp(j2pk×8/8)exp(-j2pk/8))
80 第 1 章 离散信号与系统分析基础 1-12 [ ], [ ] e 0 x k x k 分别表示一偶对称和一奇对称序列,试判断下列序列的对称性 (1) [ ] [ ] e e x k * x k (2) [ ] [ ] e o x k * x k (3) [ ] [ ] o o x k * x k 解: (1) [ ] [ ] [ ] 1 e1 e2 y k = x k * x k , [ ] [ ] [ ] 1 e1 e2 y k x n x k n n - = å - - [ ] [ ] e1 e2 x n x k n n = å + [ ] [ ] e1 e2 x n x k n n = å - - [ ] [ ] [ ] e1 e2 1 x n x k n y k n = å - = 故序列偶对称 (2) [ ] [ ] [ ] 2 o e y k = x k * x k , [ ] [ ] [ ] 2 o e y k x n x k n n - = å - - [ ] [ ] o e x n x k n n = å + [ ] [ ] o e x n x k n n = å - - [ ] [ ] [ ] o e 2 x n x k n y k n = -å - = - 故序列奇对称 (3) [ ] [ ] [ ] 3 o1 o2 y k = x k * x k , [ ] [ ] [ ] 3 o1 o2 y k x n x k n n - = å - - [ ] [ ] o1 o2 x n x k n n = -å + [ ] [ ] o1 o2 x n x k n n = å - + [ ] [ ] [ ] o o 3 x n x k n y k n = å - = 故序列偶对称 1-13 试确定下列周期为 4 的序列的 DFS 系数。 [ ] {1, 2, 0, 2; 0,1,2,3} ~x k = k = , [ ] {0,1, 0, 1; 0,1,2,3} ~ h k = - k = 解: mk k X m x k W4 3 0 [ ] ~ [ ] ~ å= = ={5, 1, -3, 1; m=0,1,2,3} mk k H m h k W4 3 0 [ ] ~ [ ] ~ å= = ={0, - 2j, 0, 2j; m=0,1,2,3} 1-14 试确定下列周期为 4 的序列的周期卷积 [ ] ~ ~ [ ] ~ [ ] ~y k = x k * h k [ ] {0,1, 0, 2; 0,1,2,3} ~x k = k = , [ ] {2, 0,1, 0; 0,1,2,3} ~ h k = k = 解: ú ú ú ú û ù ê ê ê ê ë é = ú ú ú ú û ù ê ê ê ê ë é ú ú ú ú û ù ê ê ê ê ë é = ú ú ú ú û ù ê ê ê ê ë é 5 0 4 0 2 0 1 0 0 1 0 2 1 0 2 0 0 2 0 1 2 0 1 0 [3] ~ [2] ~ [1] ~ [0] ~ y y y y 1-15 试确定下列周期序列的周期及 DFS 系数 (1) [ ] sin(p / 4) ~ 1 x k = k (2) [ ] 2sin(p / 4) cos(p / 3) ~ 2 x k = k + k 解:(1) (p / 4)/ 2p = 1/8 ; N=8 [ ] 0.5 j{exp(j2p / 8) exp( j2p / 8)} ~ 1 x k = - k - - k = -0.5 j{exp(j2pk / 8) - exp(j2pk ´8/ 8) exp(- j2pk / 8)}
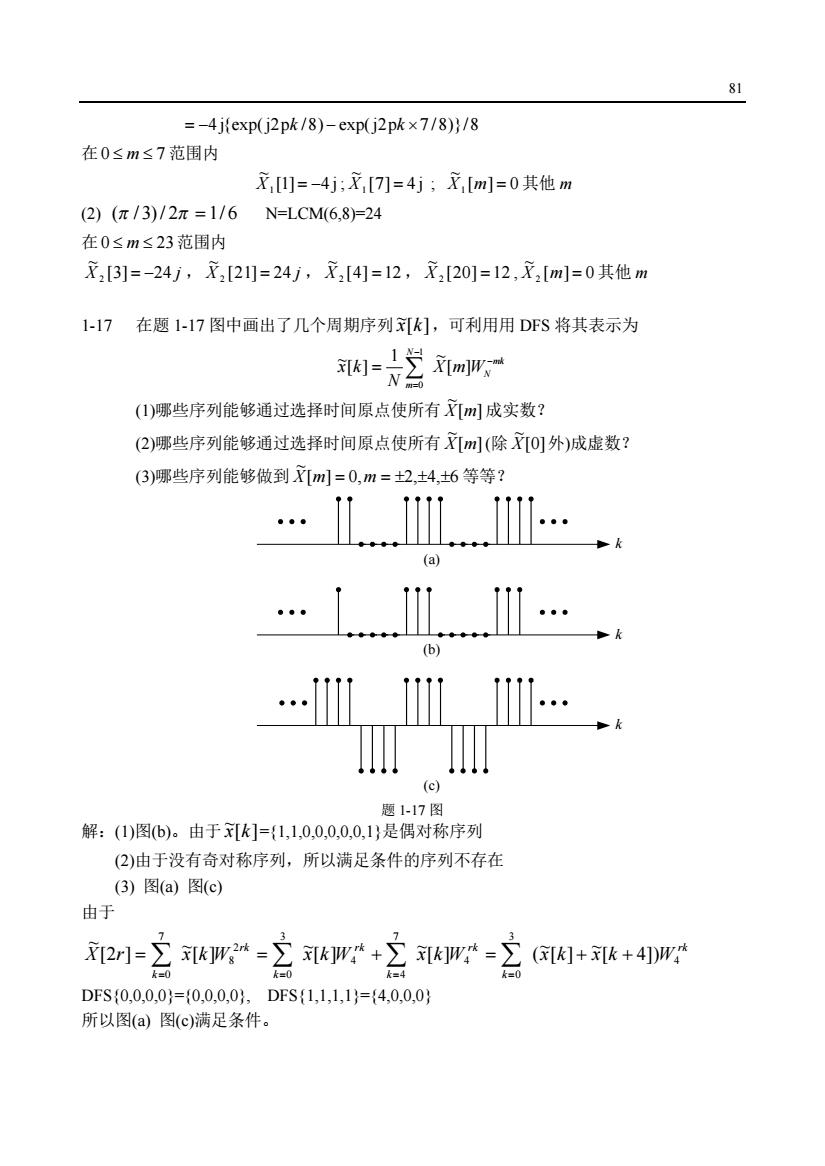
81=-4j(exp(j2pk/8)-exp(j2pk×7/8))/8在0≤m≤7范围内x,[1]=-4j;X,[7]=4jX,[m]=0其他m(2) (元 /3)/2元 =1/6N=LCM(6,8)=24在0≤m≤23范围内x,[3]=-24j,X,[2]=24j,X,[4]=12,X,[20]=12,X,[m]=0其他m1-17在题1-17图中画出了几个周期序列刘[k],可利用用DFS将其表示为[K]=X[m)Wm(1)哪些序列能够通过选择时间原点使所有X[ml成实数?(2)哪些序列能够通过选择时间原点使所有X[ml(除X[0]外)成虚数?(3)哪些序列能够做到X[m=0,m=±2,±4,±6等等?(a)(b)(c)题1-17图解:(1)图(b)。由于[k=(1,1,0,0,0,0,0,1)是偶对称序列(2)由于没有奇对称序列,所以满足条件的序列不存在(3)图(a)图(c)由于X[2r]-2 [Kjw =x[kjwrkx[kjw*+([K]+x[+4])Wk=0-0k=4foDFS(0,0,0,0)=(0,0,0,0),DFS(1,1,1,1)=(4,0,0,0)所以图(a)图(c)满足条件
81 = -4 j{exp(j2pk /8) - exp(j2pk ´7 /8)}/8 在0 £ m £ 7 范围内 [1] 4 j ~ X1 = - ; [7] 4 j ~ X1 = ; [ ] 0 ~ X1 m = 其他 m (2) (p / 3)/ 2p = 1/ 6 N=LCM(6,8)=24 在0 £ m £ 23范围内 X [3] 24 j ~ 2 = - , X [21] 24 j ~ 2 = , [4] 12 ~ X 2 = , [20] 12 ~ X 2 = , [ ] 0 ~ X 2 m = 其他 m 1-17 在题 1-17 图中画出了几个周期序列 [ ] ~x k ,可利用用 DFS 将其表示为 mk N N m X m W N x k - - = = å [ ] 1 ~ [ ] ~ 1 0 (1)哪些序列能够通过选择时间原点使所有 [ ] ~ X m 成实数? (2)哪些序列能够通过选择时间原点使所有 [ ] ~ X m (除 [0] ~ X 外)成虚数? (3)哪些序列能够做到 [ ] 0, 2, 4, 6 ~ X m = m = ± ± ± 等等? k k k (a) (b) (c) 题 1-17 图 解:(1)图(b)。由于 [ ] ~x k ={1,1,0,0,0,0,0,1}是偶对称序列 (2)由于没有奇对称序列,所以满足条件的序列不存在 (3) 图(a) 图(c) 由于 rk k X r x k W 2 8 7 0 [ ] ~ [2 ] ~ å= = rk k rk k x k W x k W4 7 4 4 3 0 [ ] ~ [ ] ~ å å = = = + rk k x k x k W4 3 0 [ 4]) ~ [ ] ~ = å ( + + = DFS{0,0,0,0}={0,0,0,0}, DFS{1,1,1,1}={4,0,0,0} 所以图(a) 图(c)满足条件