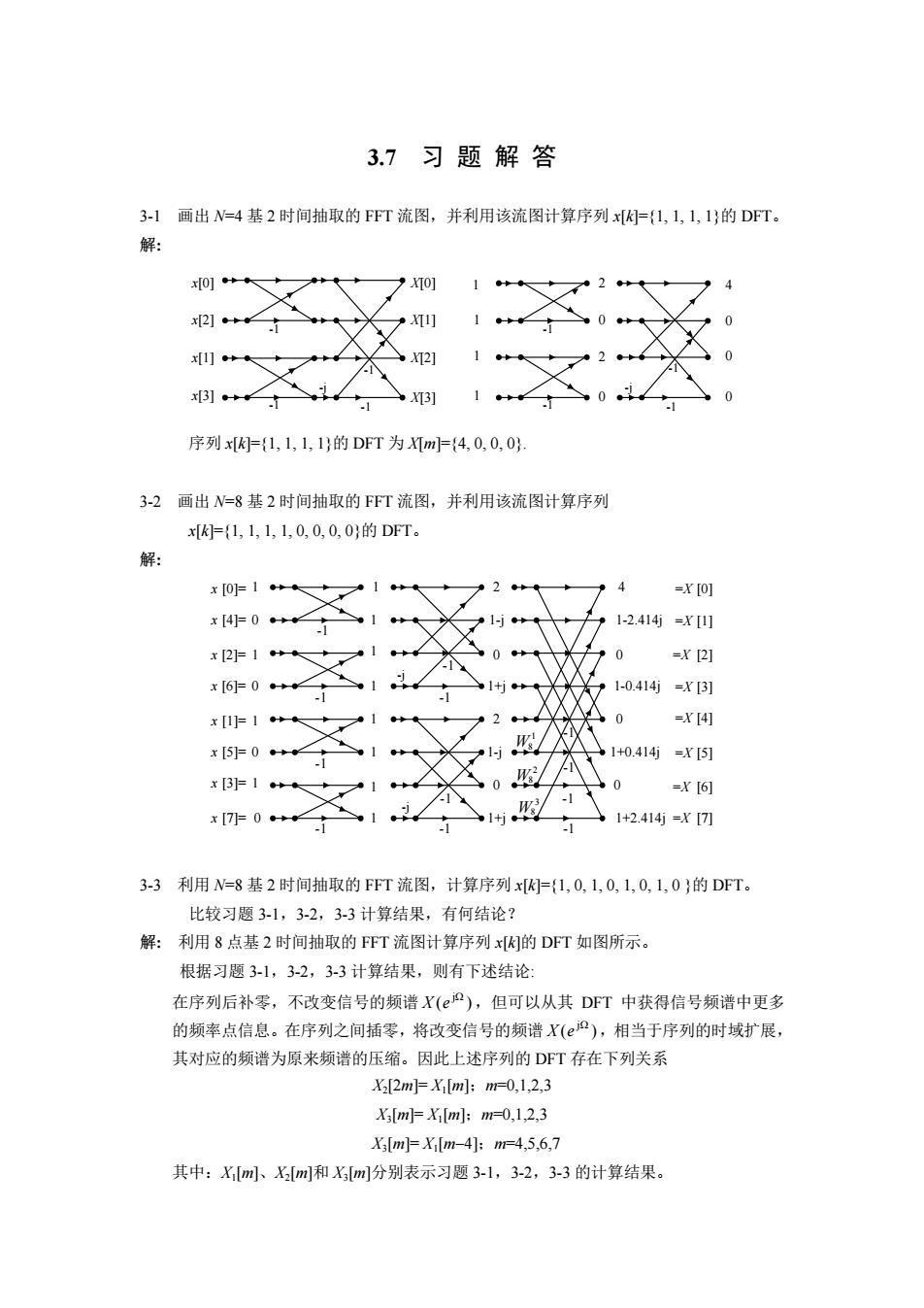
习题解答3.73-1画出N=4基2时间抽取的FFT流图,并利用该流图计算序列x[K={1,1,1,1}的DFT。解:x[0] Xox[2] XT11-/2X[2]x[1]x[3] -XT31序列x[k=(1,1,1,1)的DFT为Xm)=(4,0.0.03-2画出N=8基2时间抽取的FFT流图,并利用该流图计算序列x[K]=(1, 1, 1, 1, 0, 0, 0, 0]的 DFT。解:=X [0]x [0]= 1x[4]= 01-2.414j1-1=X[1]0=X [2]x [2]= 1 -1x [6]= 0 -1-0.414j=X [3]=X [4]0x[1}1.NW.1+0.414jx[5]= 0 -=X [5]9Wsx [3]= 100=X [6]个-1W1+2.414j =X [7]x[7- 0 .-13-3利用 N=8基2时间抽取的FFT流图,计算序列x[K)=(1,0,1,0,1,0,1,0)的DFT。比较习题3-1,3-2,3-3计算结果,有何结论?解:利用8点基2时间抽取的FFT流图计算序列x[k]的DFT如图所示。根据习题3-1,3-2,3-3计算结果,则有下述结论在序列后补零,不改变信号的频谱X(ej2),但可以从其DFT中获得信号频谱中更多的频率点信息。在序列之间插零,将改变信号的频谱X(ej),相当于序列的时域扩展,其对应的频谱为原来频谱的压缩。因此上述序列的DFT存在下列关系X[2m]=X,[m]; m=0,1,2,3X[m]=X,[m]: m=0,1,2,3X,[m]=X,[m-4]; m=4,5,6,7其中:X[m]、X[m]和X[m]分别表示习题3-1,3-2,3-3的计算结果
3.7 习 题 解 答 3-1 画出 N=4 基 2 时间抽取的 FFT 流图,并利用该流图计算序列 x[k]={1, 1, 1, 1}的 DFT。 解: -1 -1 -1 -j x[0] x[2] x[1] x[3] X[0] X[1] X[2] X[3] -1 -1 -1 -1 -j 1 1 1 1 4 0 0 0 2 0 2 0 -1 序列 x[k]={1, 1, 1, 1}的 DFT 为 X[m]={4, 0, 0, 0}. 3-2 画出 N=8 基 2 时间抽取的 FFT 流图,并利用该流图计算序列 x[k]={1, 1, 1, 1, 0, 0, 0, 0}的 DFT。 解: 1 0 1 0 1 0 1 0 1 W8 3 W8 1 1 1 1 1 1 1 1 2 0 1-j 1+j 2 0 -j -j 1-j 1+j 4 0 0 0 1-2.414j 1-0.414j 1+2.414j 1+0.414j -1 -1 -1 -1 2 W8 -1 -1 -1 -1 -1 -1 -1 -1 x [0]= x [6]= x [4]= x [2]= x [1]= x [5]= x [3]= x [7]= =X [0] =X [3] =X [1] =X [2] =X [4] =X [5] =X [6] =X [7] 3-3 利用 N=8 基 2 时间抽取的 FFT 流图,计算序列 x[k]={1, 0, 1, 0, 1, 0, 1, 0 }的 DFT。 比较习题 3-1,3-2,3-3 计算结果,有何结论? 解: 利用 8 点基 2 时间抽取的 FFT 流图计算序列 x[k]的 DFT 如图所示。 根据习题 3-1,3-2,3-3 计算结果,则有下述结论: 在序列后补零,不改变信号的频谱 ( ) jW X e ,但可以从其 DFT 中获得信号频谱中更多 的频率点信息。在序列之间插零,将改变信号的频谱 ( ) jW X e ,相当于序列的时域扩展, 其对应的频谱为原来频谱的压缩。因此上述序列的 DFT 存在下列关系 X2 [2m]= X1 [m];m=0,1,2,3 X3 [m]= X1 [m];m=0,1,2,3 X3 [m]= X1 [m-4];m=4,5,6,7 其中:X1 [m]、X2 [m]和 X3 [m]分别表示习题 3-1,3-2,3-3 的计算结果

x [0]=1=X [0]x[4]=1-X[1]X10x [2]=10=X [2]AA0x [6]=1 1 =X [3].1A07=X [4]x[1]=0·WlK0x [5]=0 X=X [5]W30O0 =X [6]x[3]=0W.x[7]=0=X [7]3-4画出N=4基2频率抽取的FFT流图,并利用其计算序列x[k}=1.-1.1.-1)的DFT。解:根据N=4基2频率抽取的FFT流图,可得X[m]={0,0,4,0]。x [0]=1·0=X [0]wo.4=X[2]3x[1]=-1 wox [2]=111.0=X[1]W:wox [3]=-1·0 =X [3]3-5试利用N=4基2时间抽取的FFT流图计算8点序列x[K)=(1,-1,1,-1,2,1,1,2)的DFT。解:根据基2时间抽取FFT算法原理,8点序列的DFTXm]可由两个4点序列的DFTX[m]和X[m]表达。如果按照序列x[k]序号的奇偶分解为x[k]和x2[k],则存在X[m]= X,[m]+W".X,[m]m=0,1,2,3X[m+4]=X,[m]-W" .X,[m]其中xi[K}-(1,1,2,1],x2[k]={-1,-1,1,2],X,[m]和X[m]可通过4点的FFT来计算,即.-1H-22+3X51X12-3X,[m]=(5,-1, 1,-1),X[m]=(1,-2+3j, 1,-2-3j)利用上述公式,可得序列x[K]的DFTX[m]为X[m)=(6, -0.293+3.535j, 1+j, -1.707 + 3.535j, 4, -1.707-3.535j, 1-j, -0.293- 3.535j)
1 1 1 1 0 0 0 0 2 0 2 0 0 0 0 0 4 0 0 0 0 0 0 0 4 4 0 0 0 0 0 0 1 W8 3 W8 -j -j -1 -1 -1 -1 2 W8 -1 -1 -1 -1 -1 -1 -1 -1 x [0]= x [6]= x [4]= x [2]= x [1]= x [5]= x [3]= x [7]= =X [0] =X [3] =X [1] =X [2] =X [4] =X [5] =X [6] =X [7] 3-4 画出 N=4 基 2 频率抽取的 FFT 流图,并利用其计算序列 x[k]={1, -1, 1, -1}的 DFT。 解: 根据 N=4 基 2 频率抽取的 FFT 流图,可得 X [m]={0, 0, 4, 0}。 1 -1 -1 -1 0 W4 2 W4 0 W4 0 W4 0 0 4 0 -1 -1 1 -1 2 -2 0 0 x [0]= x [3]= x [1]= x [2]= =X [0] =X [3] =X [2] =X [1] 3-5 试利用 N=4 基 2 时间抽取的 FFT 流图计算 8 点序列 x[k]={1, -1, 1, -1, 2, 1, 1, 2}的 DFT。 解:根据基 2 时间抽取 FFT 算法原理,8 点序列的 DFT X[m]可由两个 4 点序列的 DFT X1 [m] 和 X2 [m]表达。如果按照序列 x[k]序号的奇偶分解为 x1 [k]和 x2 [k],则存在 0,1,2,3 [ 4] [ ] [ ] [ ] [ ] [ ] 1 8 2 1 8 2 = + = - × = + × m X m X m W X m X m X m W X m m m 其中 x1 [k]={1, 1, 2, 1},x2 [k]={-1, -1, 1, 2},X1 [m]和 X2 [m]可通过 4 点的 FFT 来计算, 即 -1 -1 -1 -j 1 2 1 1 5 -1 1 -1 3 -1 2 0 -1 -1 -1 -1 -j -1 1 -1 2 1 -2+3j 1 -2-3j 0 -2 1 -3 -1 X1 [m]={5, -1, 1, -1}, X2 [m]={1, -2+3j, 1, -2-3j} 利用上述公式,可得序列 x[k]的 DFT X[m]为 X[m]={6, -0.293+3.535j, 1+j, -1.707 + 3.535j, 4, -1.707-3.535j, 1-j, -0.293- 3.535j}

如果按照序列x[k]序号的前后分解为x;[k]和x[Kk],则存在X[2m]=Z (x,[k]+x,[k])Wmkk=0,m=0,1,2,3((x,[k]-x2[kDW) wX[2m+1]=k-o同样可以由此两个4点序列的DFT表达一个8点序列的DFT。用8点DFT流图计算下列序列的8点DFT:3-6(1)x[k|= sin(k元/ 2)(2)y[k]=cos(k元/2)解:(1) x[k]=sin(k元 /2)={0, 1, 0,-1, 0, 1, 0, -1)根据8点基2时间抽取的FFT流图,可得其Xm)-{0,0,-4j,0,0,0,4j,0)x[0]=0=X [0]x [4]=0 -=X [1]10.0x[2]=04=X [2]N0x [6]=0 0=X [3]10=X [4]x[1]=1 -W!x [5]=1 =X [5]W.x[3]=-1=X [6]1Wx [7]=-1 .=X [7]11-(2)y[k]=cos(k元 / 2)=(1, 0, -1, 0, 1, 0, -1, 0)根据8点基2频率抽取的FFT流图,可得其Xm)-(0,0,4,0,0,0,4,0)0 X [0]x [0]=1 4woa088.0=X [4]x[1]=0.004wo4x [2]=-1e-20 4=X [2]W?wo.000 4 =X [6]x [3]=0 Xwox [4]=100=X[1]★W!woT.0=X[5]x [5]=0w?wo00x [6]=-10=X [3]wW?woX.0 =X [7]x[7]=03-7已知复序列v[K]=x[K]+jy[K]的8点DFT为V[0]=1-j3,V[1]=-2+ j4,V[2]=3+j7,V[3]=-4-j5,V[4]=2+j5,V[5]=-1-j2,V[6]=4-j8,V[7]=j6
如果按照序列 x[k]序号的前后分解为 x1 [k]和 x2 [k],则存在 ( ) { } , 0,1,2,3 [2 1] ( [ ] [ ]) [2 ] [ ] [ ] 1 2 8 4 3 0 1 2 4 3 0 = + = - = + å å = = m X m x k x k W W X m x k x k W k mk k mk k 同样可以由此两个 4 点序列的 DFT 表达一个 8 点序列的 DFT。 3-6 用 8 点 DFT 流图计算下列序列的 8 点 DFT: (1) x[k ] = sin(kp / 2) (2) y[k ] = cos(kp / 2) 解: (1) x[k ] = sin(kp / 2) ={0, 1, 0, -1, 0, 1, 0, -1} 根据 8 点基 2 时间抽取的 FFT 流图,可得其 X[m]={0, 0, -4j, 0, 0, 0, 4j, 0} 0 0 0 0 1 1 -1 -1 0 0 0 0 2 0 -2 0 0 0 0 0 0 4 0 0 0 0 -4j 4j 0 0 0 0 1 W8 3 W8 -j -j -1 -1 -1 -1 2 W8 -1 -1 -1 -1 -1 -1 -1 -1 x [0]= x [6]= x [4]= x [2]= x [1]= x [5]= x [3]= x [7]= =X [0] =X [3] =X [1] =X [2] =X [4] =X [5] =X [6] =X [7] (2) y[k ] = cos(kp / 2) ={1, 0, -1, 0, 1, 0, -1, 0} 根据 8 点基 2 频率抽取的 FFT 流图,可得其 X[m]={0, 0, 4, 0, 0, 0, 4, 0} 0 W8 1 W8 2 W8 3 W8 -1 1 0 -1 -1 -1 -1 0 W8 2 W8 0 W8 2 W8 -1 -1 -1 0 W8 0 W8 0 W8 0 W8 0 4 0 4 0 -1 -1 -1 -1 -1 0 1 0 -1 0 2 0 -2 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 x [0]= x [3]= x [1]= x [2]= x [4]= x [5]= x [6]= x [7]= =X [0] =X [6] =X [4] =X [2] =X [1] =X [5] =X [3] =X [7] 3-7 已知复序列 v[k]=x[k]+j y[k]的 8 点 DFT 为 V[0]= 1- j3,V[1]= -2+ j4,V[2]= 3+j7,V[3]= -4-j5, V[4]= 2+j5,V[5]= -1- j2,V[6]= 4-j8,V[7]= j6

不计算V[m]的IDFT,试确定实序列x[K]和[K]的8点DFTX[m]和Y[m]。解:根据序列DFT的对称特性,可得11X[m]=(m)+V[(-m)s]S= (1, 1- j, 3.5 + 7.5j, 2.5 1.5j, 2, 2.5 + 1.5j, 3.5- 7.5j 1+ j)[m)-V[(-m)s])Y[m]=-2j=(-3,5+j,0.5+0.5j,-3.5+1.5j5,-3.5-1.5j,-0.5-0.5j,5-j)3-8利用128点的DFT和IDFT计算一个60点序列和一个1200点序列的线性卷积。试确定利用重选相加法计算上述线性卷积所需的最少的DFT和IDFT次数。解:在利用重迭相加法时,为充分利用128点DFT计算线性卷积,可将1200点的长序列每段分为L=128+1-60=69点,共可得18段,这样每段69点序列与60点短序列的线性卷积恰好可以由128点的循环卷积计算,每个循环卷积可以由两次DFT和一次IDFT计算,故最少需要36次DFT和18次IDFT。在利用重迭保留法时,每段序列直接与60点短序列进行循环卷积,为充分利用128点DFT,可将1200点的长序列每段分为128点。由于相邻段存在60-1=59点的重选保留,且考虑第一段需补59个零,故每段只从1200点的序列中分解到128-59=69个新的数值,共可得19段[(1200+59)/69=18余17],要特别注意最后一段,因而最少需要38次DFT和19次IDFT。3-9若对模拟信号x(t)进行频谱分析,其最高频率为4kHz,抽样频率为10kHz,而且计算1024个取样点的DFT,试确定频谱取样之间的频率间隔,以及第129根谱线X[128]对应连续信号频谱的哪个频率点值?Jsam_104解:频率间隔Af。=9.7656HzN-1024128×fm=1250HzX[128]对应连续信号的频率为fi2s=N3-10已知序列x[k]=(0.5),(0≤k≤8),试计算序列x[K]在单位圆上的CZT,其中0。=元/3,@。=2元/3,M=3。解:利用MATLAB提供的函数CZt()可以计算出序列的CZT。% Compute czT of sequence x[k]=0.5^kN=9;glength of x[k]n=0:N-1;xn=(0.5).n;sita=pi/3;&phase of start pointfai=2*pi/3;%phase intervalA=exp(j*sita);%complex startingpoint
不计算 V[m]的 IDFT,试确定实序列 x[k]和 y[k]的 8 点 DFT X[m] 和 Y[m] 。 解: 根据序列 DFT 的对称特性,可得 { [ ] [( ) ]} 2 1 [ ] X m = V m +V -m 8 * = {1, -1- j, 3.5 + 7.5j, - 2.5 -1.5j, 2, - 2.5 +1.5j, 3.5 - 7.5j, -1+ j} { [ ] [( ) ]} 2 j 1 [ ] Y m = V m -V -m 8 * = {-3, 5 + j, - 0.5 + 0.5j, - 3.5+1.5j, 5, - 3.5 -1.5j, - 0.5- 0.5j, 5 - j} 3-8 利用 128 点的 DFT 和 IDFT 计算一个 60 点序列和一个 1200 点序列的线性卷积。试确 定利用重迭相加法计算上述线性卷积所需的最少的 DFT 和 IDFT 次数。 解: 在利用重迭相加法时,为充分利用 128 点 DFT 计算线性卷积,可将 1200 点的长序列 每段分为 L=128+1-60=69 点,共可得 18 段,这样每段 69 点序列与 60 点短序列的线 性卷积恰好可以由 128 点的循环卷积计算,每个循环卷积可以由两次 DFT 和一次 IDFT 计算,故最少需要 36 次 DFT 和 18 次 IDFT。 在利用重迭保留法时,每段序列直接与 60 点短序列进行循环卷积,为充分利用 128 点 DFT,可将 1200 点的长序列每段分为 128 点。由于相邻段存在 60-1=59 点的重迭保 留,且考虑第一段需补 59 个零,故每段只从 1200 点的序列中分解到 128-59=69 个新 的数值,共可得 19 段[(1200+59)/69=18 余 17],要特别注意最后一段,因而最少需要 38 次 DFT 和 19 次 IDFT。 3-9 若对模拟信号 x(t) 进行频谱分析,其最高频率为 4kHz,抽样频率为 10kHz,而且计算 1024 个取样点的 DFT,试确定频谱取样之间的频率间隔,以及第 129 根谱线 X[128]对 应连续信号频谱的哪个频率点值? 解:频率间隔 1024 104 sam D c = = N f f =9.7656 Hz X[128]对应连续信号的频率为 1250Hz 128 sam 128 = ´ = N f f 3-10 已知序列 k x[k ] = (0.5) , (0 £ k £ 8) ,试计算序列 x[k] 在单位圆上的 CZT,其中 / 3 2 / 3 3 q 0 = p ,j 0 = p ,M = 。 解:利用 MATLAB 提供的函数 czt()可以计算出序列的 CZT。 % Compute CZT of sequence x[k]=0.5^k N=9; %length of x[k] n=0:N-1; xn=(0.5).^n; sita=pi/3; %phase of start point fai=2*pi/3; %phase interval A=exp(j*sita); %complex starting point

W=exp(-j*fai);%complex ratio between pointsM=3;&lengthof czty=czt(xn,M,W,A)%call czt function运行结果y为1.002-0.578510.6681.002+0.5785i3-11若某DSP硬件系统只提供最多2048点的FFT程序,试推导利用2048点的FFT程序计算8192点的FFT和IFFT的计算表达式。解:在许多实际DSP系统中,由于资源限制,只能提供有限点的FFT算法。但根据FFT算法原理,可以利用N点序列的DFT来实现2N点序列的DFT。对于长度为2N的序列x[K]进行时间抽取,即将其分解为两个长度N点的序列,即x[k]=x[2k], k =0,1,..N-1x2[k]=x[2k+1], k = 0,],...N-1其中,x[K]是序列x[K]中的偶数点构成的序列,x[]是序列x[K]中的奇数点构成的序列。分别利用N点FFT算法计算出序列x,[K]的DFTX[m]和序列x[K]的DFTX[m],则序列x[K]的DFTX[m]可以由X,[m]和X[m]表达为X[m]= X,[m]+W"·X,[m]m=0,1...N-1X[m+N/2]=X,[m]-W"·X,[m]从而可以由两次N点的FFT计算实现2N点的FFT。如果序列x[k]为实序列,这两个N点的实序列x,[k]和x[k]可以构成一个N点的复序列y[K]=x,[K]+jx?[K],从而通过一次N点FFT就可以计算出相应的X,[m]和X[m]。如此类推,可以利用两个2N点FFT来实现一个4N点的FFT,从而可以利用N点的FFT程序实现4N点序列的DFT的计算
W=exp(-j*fai); %complex ratio between points M=3; %length of czt y=czt(xn,M,W,A) %call czt function 运行结果 y 为 1.002-0.5785i 0.668 1.002+0.5785i 3-11 若某 DSP 硬件系统只提供最多 2048 点的 FFT 程序,试推导利用 2048 点的 FFT 程序 计算 8192 点的 FFT 和 IFFT 的计算表达式。 解: 在许多实际 DSP 系统中,由于资源限制,只能提供有限点的 FFT 算法。但根据 FFT 算法原理,可以利用 N 点序列的 DFT 来实现 2N 点序列的 DFT。 对于长度为 2N 的序列 x[k]进行时间抽取,即将其分解为两个长度 N 点的序列,即 [ ] [2 ], 0,1, 1 x1 k = x k k = KN - [ ] [2 1], 0,1, 1 x2 k = x k + k = KN - 其中,x1 [k]是序列 x[k]中的偶数点构成的序列, x2 [k]是序列 x[k]中的奇数点构成的序列。 分别利用 N 点 FFT 算法计算出序列 x1 [k]的 DFT X1 [m]和序列 x2 [k]的 DFT X2 [m],则 序列 x[k]的 DFT X[m]可以由 X1 [m]和 X2 [m]表达为 0,1 1 [ / 2] [ ] [ ] [ ] [ ] [ ] 1 2 1 2 = - + = - × = + × m N X m N X m W X m X m X m W X m m N m N K 从而可以由两次 N 点的 FFT 计算实现 2N 点的 FFT。 如果序列 x[k]为实序列,这两个 N 点的实序列 x1 [k]和 x2 [k]可以构成一个 N 点的复序 列 y[k]=x1 [k]+jx2 [k],从而通过一次 N 点 FFT 就可以计算出相应的 X1 [m]和 X2 [m]。 如此类推,可以利用两个 2N 点 FFT 来实现一个 4N 点的 FFT,从而可以利用 N 点 的 FFT 程序实现 4N 点序列的 DFT 的计算