第1 章信号的时域分析1.1连续信号的时域分析连续时间信号的时域分析就是将不同形式的信号波形用不同的时间函数来描述,例如:连续周期信号通过CTFS分解为不同谐波成分的三角函数或指数函数之和,连续非周期信号分解为频率无限密集的虚指数函数的线性组合,即ICTFT。在时域还可以把实信号分解为奇信号与偶信号之和等等。其中常用的连续时间信号是信号时域分析的基础,在此用Matlab提供的函数可以产生此类常用的连续时间信号。例1.产生幅度为2,频率为4Hz,初相为元/6的正弦信号解:A=2;f0=4;phi=pi/6;w0=2*pi*fO;t=0:0.001:1x=A*sin(w0*t+phi);plot(t,x);ylabel(x(t));xlabel(t);150.5爱C0.51.5210.10.6E0.20.507009y(t)例2:产生一阶跃信号x(t)=u(t)解:t=-1:0.01:5;x=(t>=0);
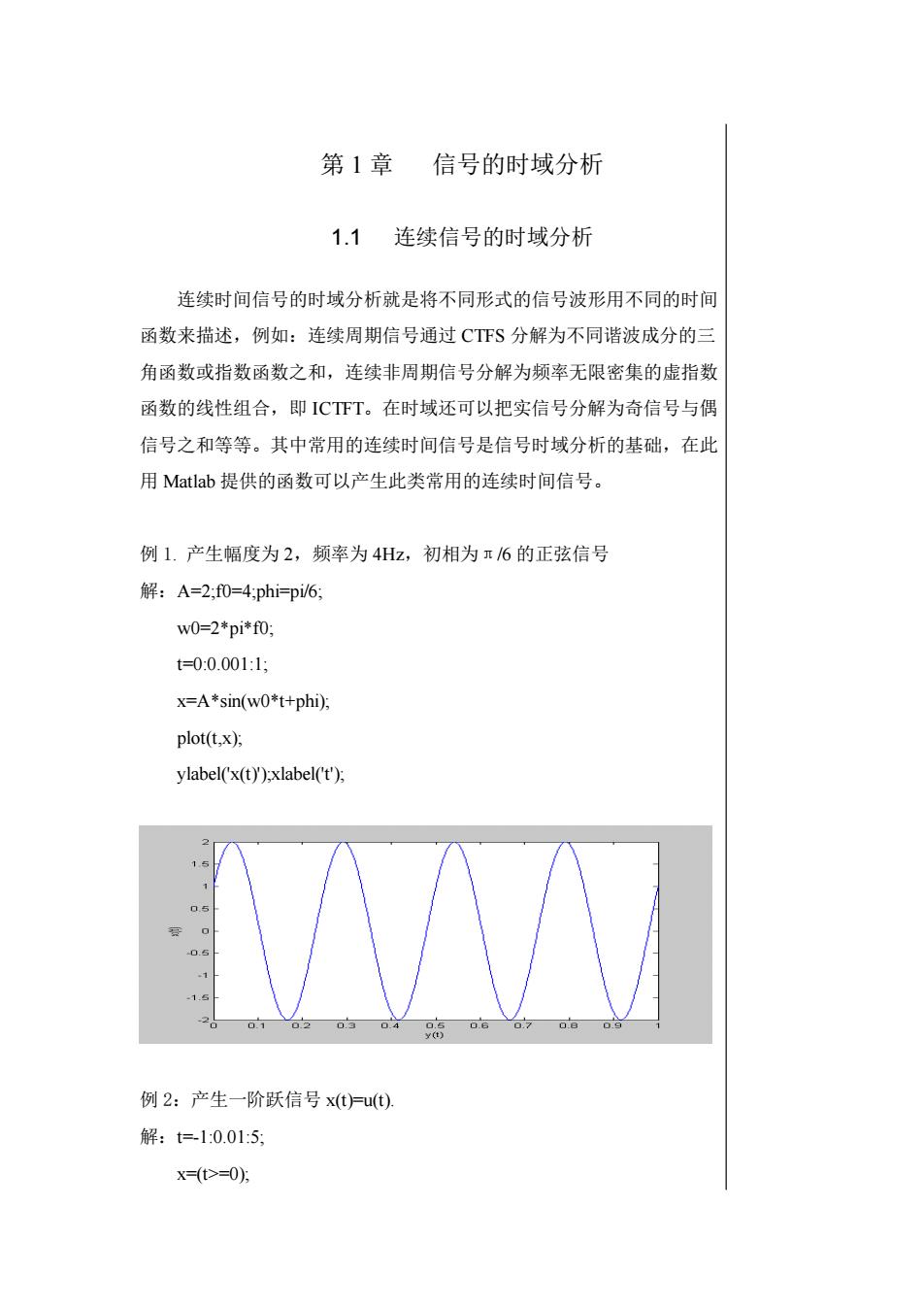
第 1 章 信号的时域分析 1.1 连续信号的时域分析 连续时间信号的时域分析就是将不同形式的信号波形用不同的时间 函数来描述,例如:连续周期信号通过 CTFS 分解为不同谐波成分的三 角函数或指数函数之和,连续非周期信号分解为频率无限密集的虚指数 函数的线性组合,即 ICTFT。在时域还可以把实信号分解为奇信号与偶 信号之和等等。其中常用的连续时间信号是信号时域分析的基础,在此 用 Matlab 提供的函数可以产生此类常用的连续时间信号。 例 1. 产生幅度为 2,频率为 4Hz,初相为π/6 的正弦信号 解:A=2;f0=4;phi=pi/6; w0=2*pi*f0; t=0:0.001:1; x=A*sin(w0*t+phi); plot(t,x); ylabel('x(t)');xlabel('t'); 例 2:产生一阶跃信号 x(t)=u(t). 解:t=-1:0.01:5; x=(t>=0);
plot(t,x);axis([-2,6,-0.1,1.1]),0.8D.E0.4例3:产生一语音信号解:t=0:0.01:1;plot(t,randn(1,length(t);2.5w设计题目:用Matlab产生下列信号并与人工分析结果进行比较:-1<t<10(1) r(t)=tu(t)-1<t<1(2)x (t)=1+cos10 t(3)x (t)=(5e-t- 5e-3t) u (t)-1<t<50<t<5(4)x (t)=cos(2 π t) cos(20 π t)(5) x(t)=sin(t)/t-10<t<10
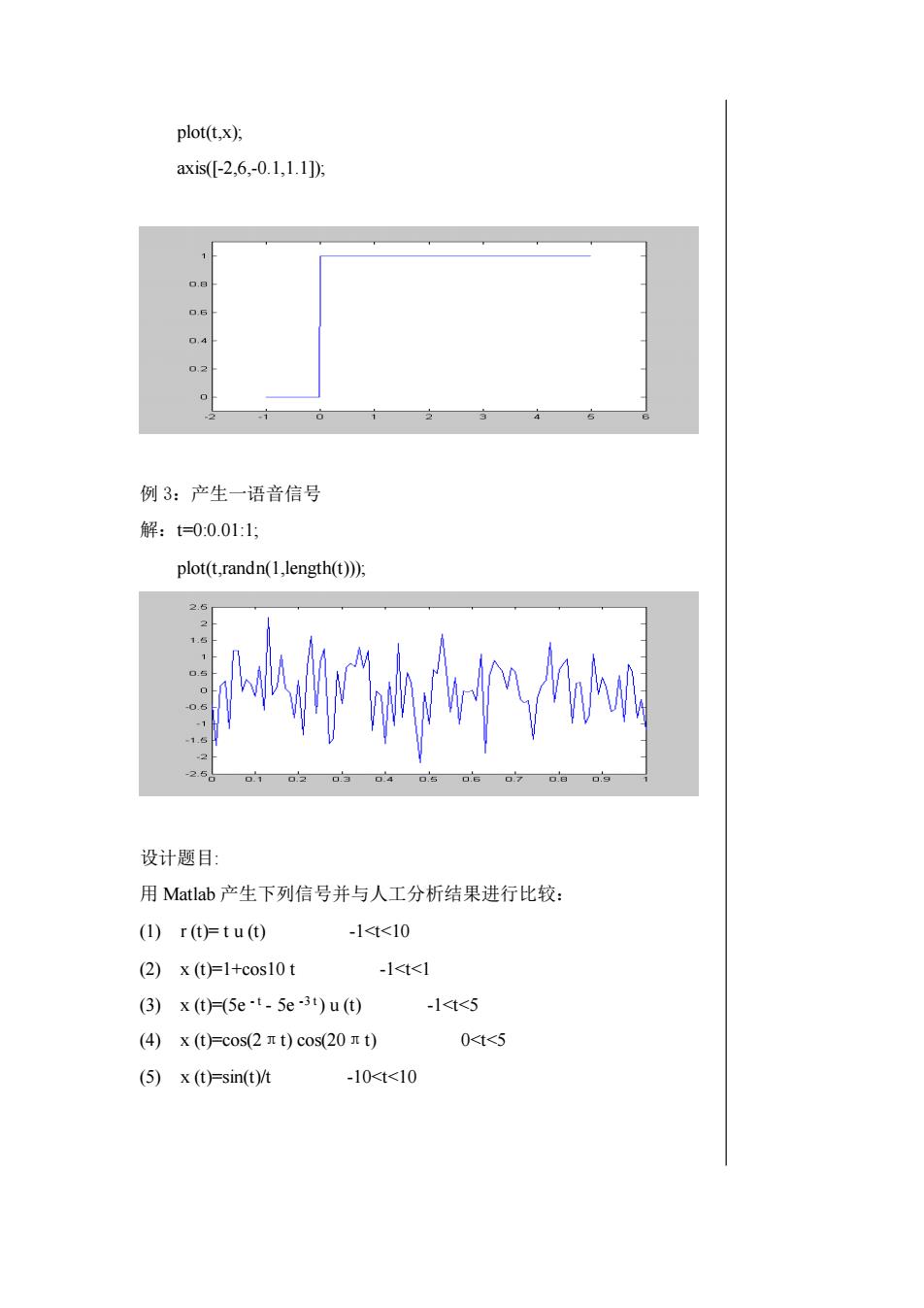
plot(t,x); axis([-2,6,-0.1,1.1]); 例 3:产生一语音信号 解:t=0:0.01:1; plot(t,randn(1,length(t))); 设计题目: 用 Matlab 产生下列信号并与人工分析结果进行比较: (1) r (t)= t u (t) -1<t<10 (2) x (t)=1+cos10 t -1<t<1 (3) x (t)=(5e - t - 5e -3 t ) u (t) -1<t<5 (4) x (t)=cos(2πt) cos(20πt) 0<t<5 (5) x (t)=sin(t)/t -10<t<10
1.2离散时间序列的时域分析及信号的运算常见基本离散序列有正弦序列、指数序列、矩形脉冲序列、单位脉冲序列与单位阶跃序列等。这些序列可以由Matlab产生:("n+")例1:产生一正弦序列y(n)=2sin("66解:A=2;N=15;phi=pi/6;omega=pi/6;n=-10:10;y=A*sin(omega*n+phi);stem(n.y),ylabel(y(n));xlabel(n'),在信号的时域分析中,重要的一项内容为信号的运算,包括信号的相加、相乘、乘方、卷积、相关等运算,以及求解信号的功率与能量。连续时间信号能量及功率的求解公式为:信号的能量:E=「|x(t)’dt=[x(t)x*(t)dt度 Ix(t)°dt=度x(t)x*(t)dtp=-信号的功率:因果离散序列能量及功率的求解公式为:序列的能量:E=≥Ix(n) /’=2 x(n) x* (n)n=07=
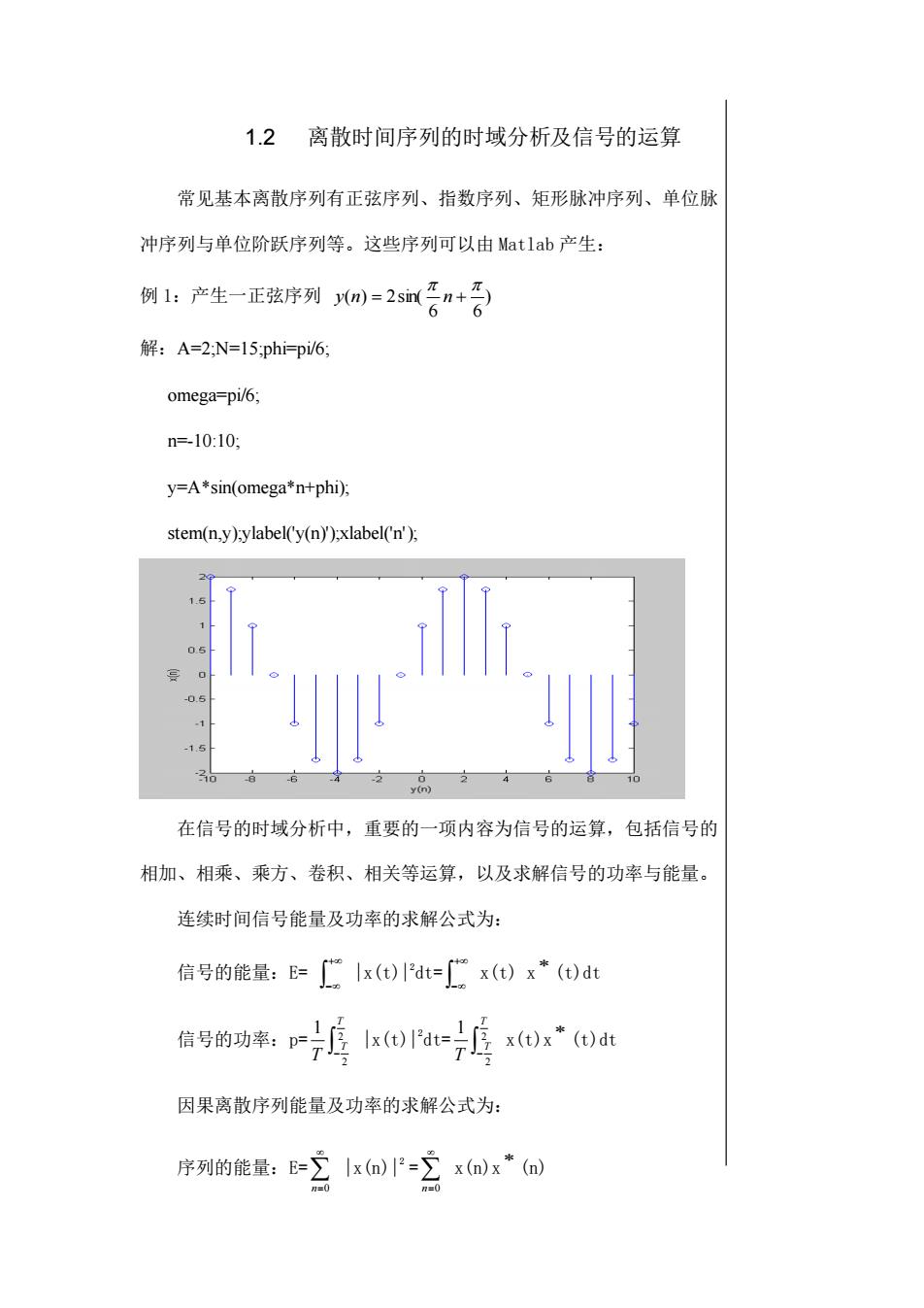
1.2 离散时间序列的时域分析及信号的运算 常见基本离散序列有正弦序列、指数序列、矩形脉冲序列、单位脉 冲序列与单位阶跃序列等。这些序列可以由 Matlab 产生: 例 1:产生一正弦序列 ) 6 6 ( ) 2sin( y n = n + 解:A=2;N=15;phi=pi/6; omega=pi/6; n=-10:10; y=A*sin(omega*n+phi); stem(n,y);ylabel('y(n)');xlabel('n'); 在信号的时域分析中,重要的一项内容为信号的运算,包括信号的 相加、相乘、乘方、卷积、相关等运算,以及求解信号的功率与能量。 连续时间信号能量及功率的求解公式为: 信号的能量:E= + − |x(t)|2 dt= + − x(t) x (t)dt 信号的功率:p= − 2 2 1 T T T |x(t)|2 dt= − 2 2 1 T T T x(t)x (t)dt 因果离散序列能量及功率的求解公式为: 序列的能量:E= n=0 |x(n)|2 = n=0 x(n)x (n)

序列的功率:p=!岁[x(n) [3=x(n)x* (n)NN0例2:求解x(t)=e"t[u(t)-u(t-1)]在[0,1]时间内的能量。解:首先建立一内部函数计算信号的瞬时能量:functionf-powert(t)f=(abs(exp(-1.*t).^2;计算信号在[0,1]时间内的能量:power-t=quad(powert",o,1)power-t=0.4323例3:已知序列x(n)=0.8u(n),计算前十点的能量。解:N=10;n=0:N-1;x=(0. 8). n;e=sum(abs(x).2)e =2.7458通过计算,序列前十点的能量占总能量的98.85%。离散序列的线性卷积和运算:例4:若x(n)=[1,1,1,1,0,0,],计算离散序列的卷积y(n)=x(n)*x(n)。解:x=[1,1,1,1,0,0,];y=conv(x,x);subplot(2,1,1);stem([0:length(x)-1],x),ylabel(x(n));xlabel(Time index n');subplot(2,1,2);stem([0:length(y)-1],y),ylabel(y(n)=x(n)*x(n));xlabel(Time index n');
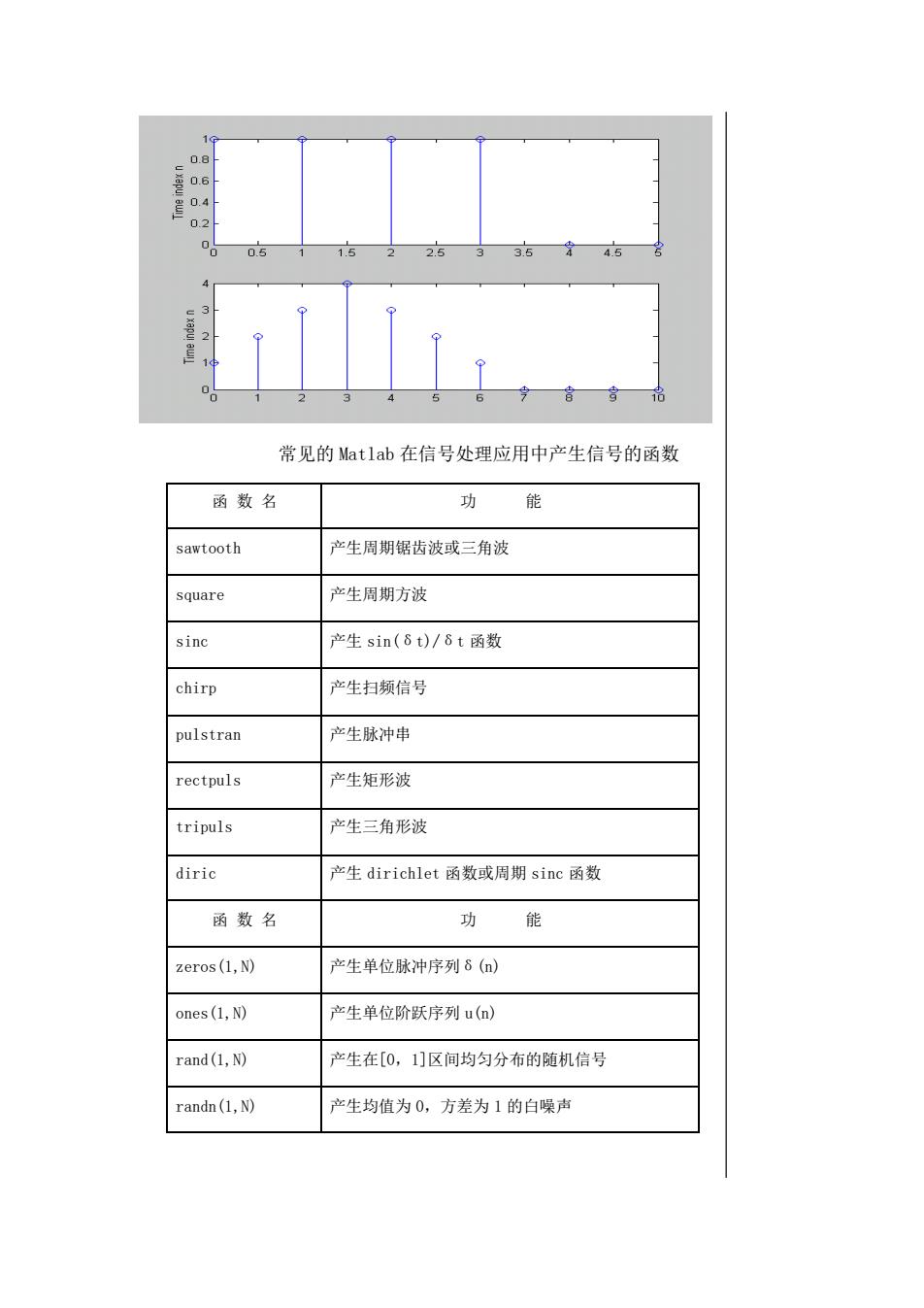
序列的功率:p= − = 1 0 1 N N n |x(n)|2 = − = 1 0 1 N N n x(n)x (n) 例 2:求解 x(t)=e -t [u(t)-u(t-1)]在[0,1]时间内的能量。 解:首先建立一内部函数计算信号的瞬时能量: function f=powert(t) f=(abs(exp(-1.*t))).^2; 计算信号在[0,1]时间内的能量: power-t=quad(`powert`,0,1) power-t=0.4323 例 3:已知序列 x(n)=0.8 n u(n),计算前十点的能量。 解:N=10; n=0:N-1; x=(0.8).^n; e=sum(abs(x).^2) e =2.7458 通过计算,序列前十点的能量占总能量的 98.85%。 离散序列的线性卷积和运算: 例 4:若 x(n)=[1,1,1,1,0,0,], 计算离散序列的卷积 y(n)=x(n)*x(n)。 解:x=[1,1,1,1,0,0,]; y=conv(x,x); subplot(2,1,1);stem([0:length(x)-1],x); ylabel('x(n)');xlabel('Time index n'); subplot(2,1,2);stem([0:length(y)-1],y); ylabel('y(n)=x(n)*x(n)');xlabel('Time index n');
EEE0.20.5uxapurs常见的Matlab在信号处理应用中产生信号的函数功能函数名产生周期锯齿波或三角波sawtooth产生周期方波squaresinc产生sin(8t)/8t函数chirp产生扫频信号产生脉冲串pulstran产生矩形波rectpulstripuls产生三角形波diric产生dirichlet函数或周期sinc函数功能函数名zeros(1,N)产生单位脉冲序列8(n)ones(1, N)产生单位阶跃序列u(n)rand(1, N)产生在[0,1]区间均匀分布的随机信号randn(1, N)产生均值为0,方差为1的白噪声
常见的 Matlab 在信号处理应用中产生信号的函数 函 数 名 功 能 sawtooth 产生周期锯齿波或三角波 square 产生周期方波 sinc 产生 sin(δt)/δt 函数 chirp 产生扫频信号 pulstran 产生脉冲串 rectpuls 产生矩形波 tripuls 产生三角形波 diric 产生 dirichlet 函数或周期 sinc 函数 函 数 名 功 能 zeros(1,N) 产生单位脉冲序列δ(n) ones(1,N) 产生单位阶跃序列 u(n) rand(1,N) 产生在[0,1]区间均匀分布的随机信号 randn(1,N) 产生均值为 0,方差为 1 的白噪声