
离散时间Fourier变换(DTFT)·DTFT的定义·DTFT性质·DTFT的频域抽样用MATLAB计算DTFT
•DTFT的定义 •DTFT性质 •DTFT的频域抽样 •用MATLAB计算DTFT 离散时间Fourier变换(DTFT)

DTFT的定义80x[k]e-jkDTFT:X(ej°)=k=-00特点:1)X(e J?)是连续的2)X(e j2)是周期为2元的周期函数IDTFT:X(ej")ejk?d?x[k] 2元2元ojd(22)) = Xr(ej?)+ jX,(ej°)X(ej°)=d(②) 的主值(principal value)一元<(2)<≤元
DTFT的定义 特点:1)X(e jW )是连续的 2)X(e jW )是周期为2p的周期函数 IDTFT: W p W W p x k X e e d j jk ( ) 2 1 [ ] 2 = ( ) ( ) ( ) ( ) W W (W) W jW I j R j j j X e = X e e = X e + j X e (W) 的主值(principal value) -p(W)p j k k j X e x k e W - W =- DTFT: ( ) = [ ]
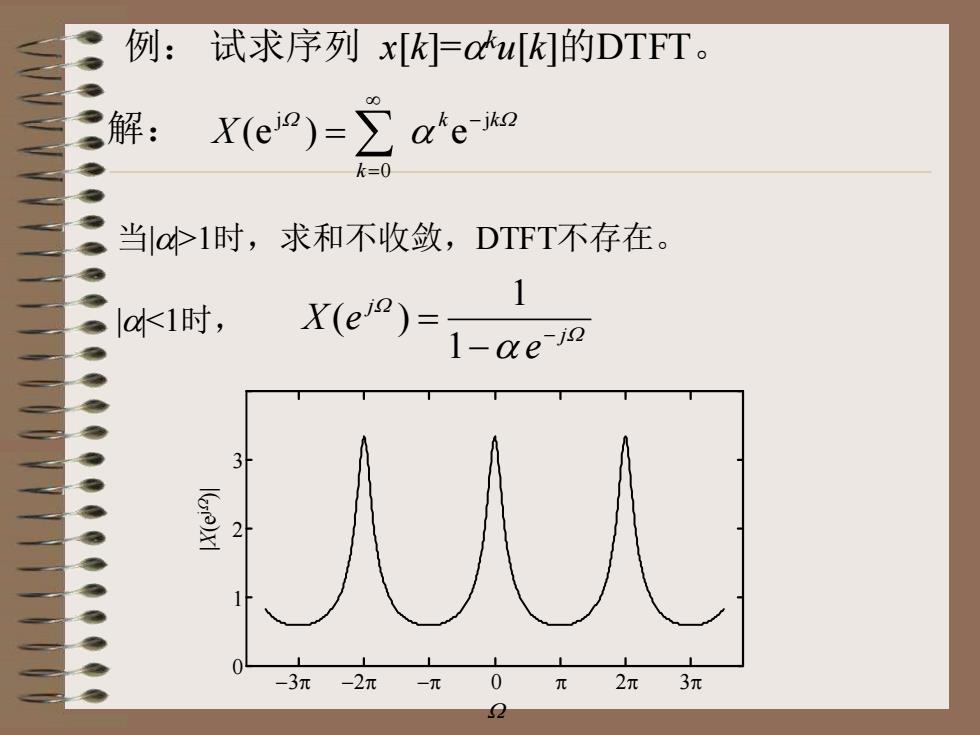
例:试求序列 x[K]=αtu[K]的DTFT。X(ei°)= αhe-ik?解:k=0当|α>1时,求和不收敛,DTFT不存在。1X(ej")[α<1时,l-αe-j?3EM0-3元-2元2元3元元一元2
例: 试求序列 x[k]=aku[k]的DTFT。 W W a k k k X j 0 j (e ) e - = = 当|a|>1时,求和不收敛,DTFT不存在。 |a|<1时, W W a j j e X e - - = 1 1 ( ) 0 3p 0 1 2 3 -3p -2p -p p 2p |X(ejW )| W 解:

DTFT的收敛性x[k]e-j2k定义X(eig)的部分和 X(ej)=k=-N若Z [x[k]Λ8k则 lim|X(ej°)-X(ei°) =0N-00Z [x[k]若<8则 lim " X(ei°)-X(ej°) d2=0N-00
DTFT的收敛性 定义X(ejW)的部分和 k N k N N X x k jW jW (e ) [ ]e - =- = x[k] k 若 lim (e ) (e ) 0 j j - = → W W N N 则 X X 2 x[k] k 若 lim (e ) (e ) d 0 2 j j - = → - W W W p p N N 则 X X
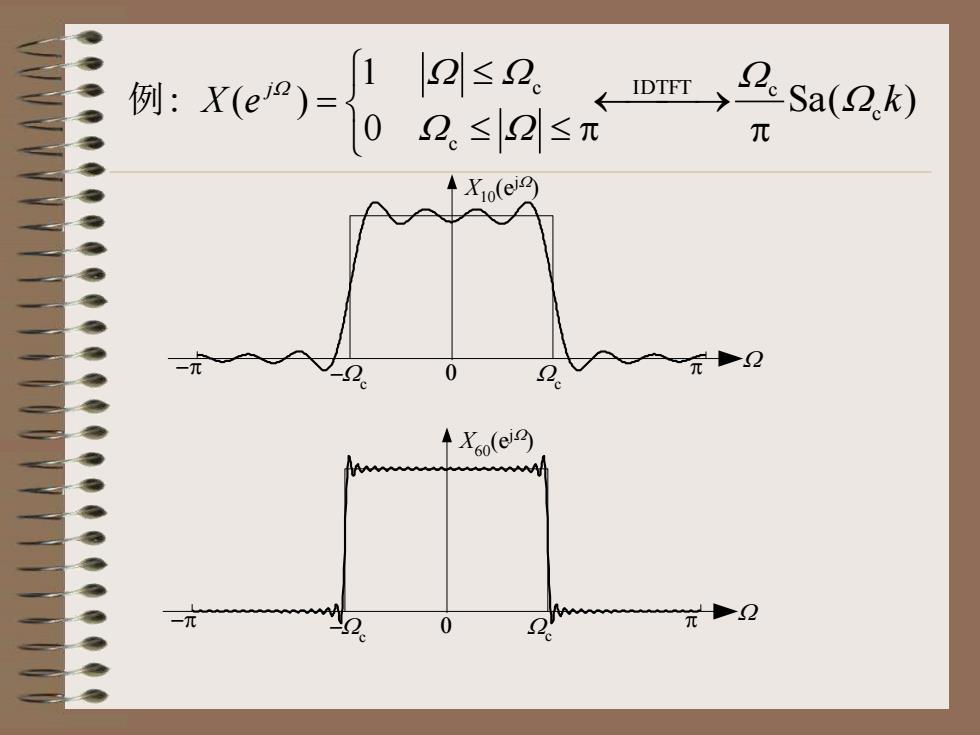
[2|≤20IDTFTSa(例:1-2.≤2|≤元元0元0
p = W W W W W c c 0 1 : ( ) j 例 X e Sa( ) c IDTFT c W k W p ⎯⎯→ X10(ejW ) -p p W Wc -Wc X60(ejW ) -p p W Wc -Wc