
第3章离散傅里叶变换快速算法(FFT)问题的提出4点序列(2,3,3,2)DFT的计算复杂度Nx[kjWkm,m=0,],..N-1X[m]=k=0X[0]=2W+3W+3W+2W=10X[1]=2W+3W+3W?+2W =-1- jX[2] =2W+3W?+3W+2W=0X[3]=2W°+3W?+3W+2W=-1+j复数加法N(N-1)复数乘法N2如何提高DFT的运算效率?解决问题的思路1.将长序列DFT分解为短序列的DFT2.利用旋转因子的周期性、对称性、可约性。旋转因子Wkm的性质1)周期性W(k+N)m=Wk(m+N)=Wh2)对称性mk+2 =-Wmk(wm) =WmkWN3)可约性Wmk=WrmknNWw=Wwml",N/n为整数解决问题的方法将时域序列逐次分解为一组子序列,利用旋转因子的特性,由子序列的DFT来实现整个序列的DFT。基2时间抽取(Decimationintime)FFT算法[x[2r]N.-1r=0,1,.x[k]→2[x[2r+1]基2频率抽取(Decimationinfrequency)FFT算法[X[2m]X[m]-X[2m+1]
第 3 章 离散傅里叶变换快速算法(FFT) 问题的提出 4 点序列{2,3,3,2} DFT 的计算复杂度 [ ] [ ] , 0,1, 1 1 0 = = − − = X m x k W m N km N N k [0] 2 3 3 2 10 0 0 0 0 X = WN + WN + WN + WN = X W W W W j [1] = 2 N + 3 N + 3 N + 2 N = −1− 0 1 2 3 [2] 2 3 3 2 0 0 2 4 6 X = WN + WN + WN + WN = X W W W W j [3] = 2 N + 3 N + 3 N + 2 N = −1+ 0 3 6 9 复数加法 N(N-1) 复数乘法 N 2 如何提高 DFT 的运算效率? 解决问题的思路 1. 将长序列 DFT 分解为短序列的 DFT 2. 利用旋转因子 的周期性、对称性、可约性。 旋转因子 km WN 的性质 1)周期性 km N k m N N k N m WN =W =W ( + ) ( + ) 2) 对称性 mk N N mk WN = −W + 2 ( ) mk N km WN W − = 3)可约性 nmk nN mk WN =W WN mk =WN mk / n / n , N / n为整数 解决问题的方法 将时域序列逐次分解为一组子序列,利用旋转因子的特性, 由子序列的 DFT 来实现整个序列的 DFT。 基 2 时间抽取(Decimation in time)FFT 算法 1 2 0,1, [2 1] [2 ] [ ] = − + → N r x r x r x k 基 2 频率抽取(Decimation in frequency)FFT 算法 + → [2 1] [2 ] [ ] X m X m X m
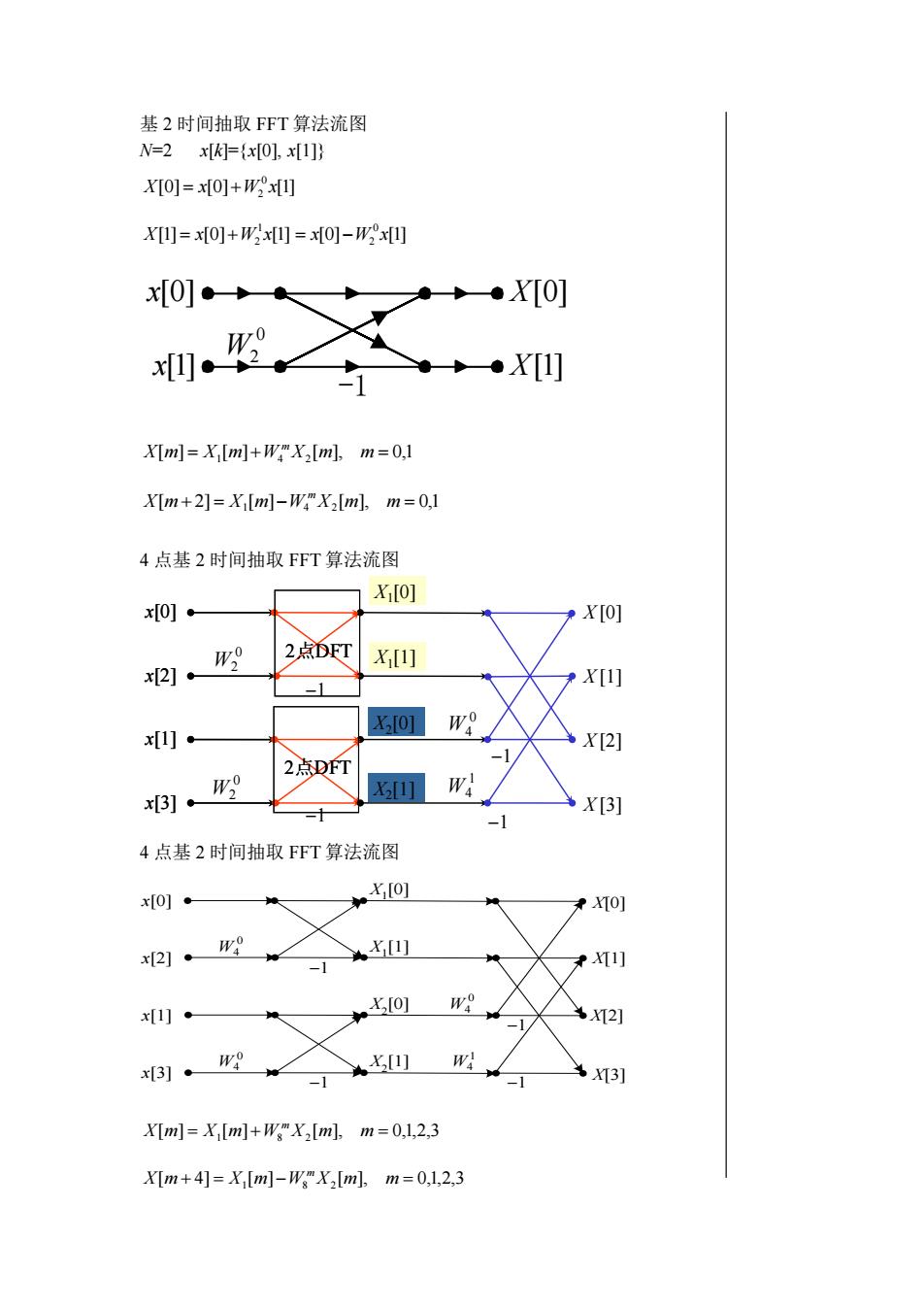
基2时间抽取FFT算法流图N=2 x[K]={x[0], x[1]]X[0] = x[0]+W,x[]X[1] = x[0]+ W,x[1] = x[0] -W x[]x[0].10wax[1]X11X[m]=X,[m]+W"X,[m],m=0,1X[m+2]=X[m]-W"X,[m],m=0,14点基2时间抽取FFT算法流图X,[0]x[0] :X[0]2点DFTw?X,[1]x[2] X[1]woX.0]x[1] X[2]2点DFTwW![11x[3]X[3]-14点基2时间抽取FFT算法流图X,[0]x[0]X[0]woX,[1]x[2] X[1]woX,[0]x[1] :X[2]woW!X,[1]x[3]X[3]X[m]=X,[m]+W"X,[m], m=0,1,2,3X[m+4]=X,[m]-WmX,[m], m=0,1,2,3
基 2 时间抽取 FFT 算法流图 N=2 x[k]={x[0], x[1]} [0] [0] [1] 0 2 X = x +W x [1] [0] [1] 1 2 X = x +W x [0] [1] 0 2 = x −W x X[m] = X1 [m]+W4 X2 [m], m = 0,1 m X[m+ 2] = X1 [m]−W4 X2 [m], m = 0,1 m 4 点基 2 时间抽取 FFT 算法流图 x[0] x[2] x[1] x[3] X1 [0] X1 [1] X2 [0] X2 [1] 2点DFT 2点DFT −1 −1 −1 −1 0 W4 1 W4 0 W2 0 W2 X [0] X [1] X [2] X [3] 4 点基 2 时间抽取 FFT 算法流图 X[m] = X1 [m]+W8 X2 [m], m = 0,1,2,3 m X[m + 4] = X1 [m]−W8 X2 [m], m = 0,1,2,3 m x[0] x[1] X[0] -1 0 W2 X[1] x[0] x[2] x[1] x[3] −1 −1 −1 −1 X[0] X[2] X[1] X[3] X1 [0] X2 [0] X1 [1] X2 [1] 0 W4 1 W4 0 W4 0 W4

8点基2时间抽取FFT算法流图X,[0]x[0] :X[0]X,[], X[1]x[2] :4点DFTX,[2] X[2]x[4] ·X,[3] X[3]x[6] :X,[0]woX[4]x[1] :xw!X[5]x[3] ·4点DFTX[2] W2x[5] ..X[6]X,[3]W]X[7]x[7] :8点基2时间抽取FFT算法流图X,[0]X.[O]x[0] .X[0]2点DFTX[]]X.[1]x[4]9 X[1]owoX,[2]x[2] . X[2]2点DFTX[w!X,[3]x[6] · X[3]X[0] wX..[o]X[4].x[1].2点DFTX]wX..[1]X[5].x[5] n[0] woX[2]W2.X[6].x[3] .2点DFTljw!X[3] w3X[7].x[7]3. 1基2时间抽取FFT算法第三级第二级第一级[0] .X[0]woX[1]x[4]-wox[2] . X[2]woW?X[3]x[6]-wox[1].X[0]WoW!X[1]x[5]wow?x[3] .+X[2]woW?w3+X[3][7]-
8 点基 2 时间抽取 FFT 算法流图 4点DFT 4点DFT x[0] x[2] x[4] x[6] x[0] x[2] x[4] x[6] x[1] x[3] x[5] x[7] x[1] x[3] x[5] x[7] X1[0] X1[1] X1[2] X1[3] X2[0] X2[1] X2[2] X2[3] X [0] X [1] X [2] X [3] X [4] X [5] X [6] X [7] −1 −1 −1 −1 0 W8 1 W8 2 W8 3 W8 8 点基 2 时间抽取 FFT 算法流图 4点DFT 4点DFT x[0] x[2] x[4] x[6] x[0] x[2] x[4] x[6] x[1] x[3] x[5] x[7] x[1] x[3] x[5] x[7] X1[0] X1[1] X1[2] X1[3] X2[0] X2[1] X2[2] X2[3] X [0] X [1] X [2] X [3] X [4] X [5] X [6] X [7] −1 −1 −1 −1 0 W8 1 W8 2 W8 3 W8 2点DFT 2点DFT x[0] x[4] x[2] x[6] −1 1 W4 X11[0] X11[1] X12[0] X12[1] 0 W4 2点DFT 2点DFT −1 −1 X21[0] X21[1] X22[0] X22[1] x[1] x[5] x[3] x[7] 1 W4 0 W4 3.1 基 2 时间抽取 FFT 算法 x[0] x[4] x[2] x[6] X[0] X[2] X[1] X[3] −1 −1 −1 −1 0 W8 0 W8 0 W8 x[1] x[5] x[3] x[7] X[0] X[2] X[1] X[3] −1 −1 −1 −1 0 W8 0 W8 0 W8 1 W8 0 W8 3 W8 2 W8 2 W8 2 W8 −1 −1 −1 −1 第一级 第二级 第三级
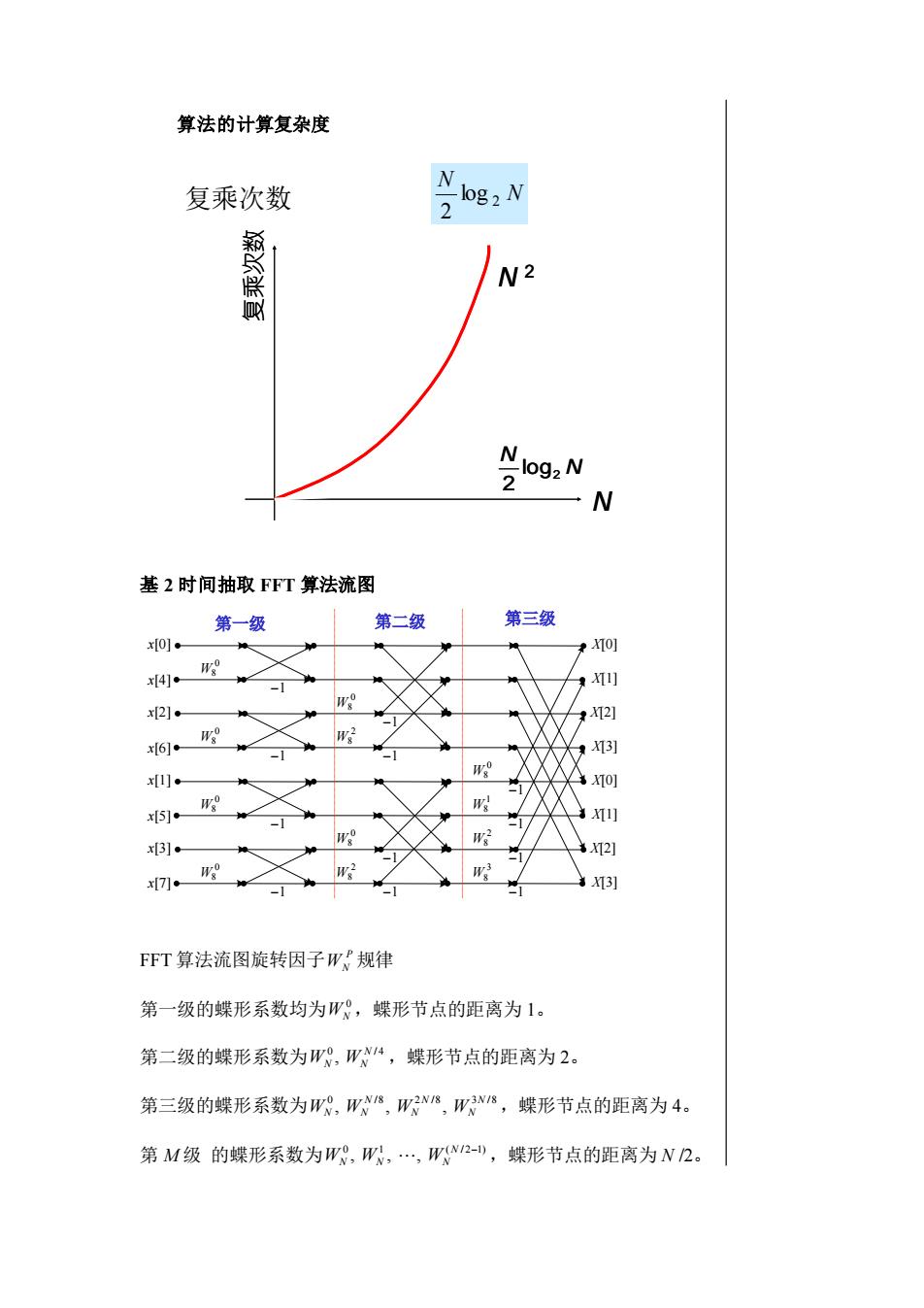
算法的计算复杂度Nlog2N复乘次数2N2Nlog2N2N基2时间抽取FFT算法流图第三级第二级第一级x[0] .X[0]woX[1]x[4] ·wox[2] . X[2]W2woX[3]x[6]wox[1].X[0]woW!X[1]x[5].wow?+X[2]x[3] .-wwow3X[3]x[7].FFT算法流图旋转因子WP规律第一级的蝶形系数均为W°,蝶形节点的距离为1。第二级的蝶形系数为W",WN/4,蝶形节点的距离为2。第三级的蝶形系数为Wo,WN/sW2N/8W3N/8,蝶形节点的距离为4。第M级的蝶形系数为W",W",,W(N/2-1),蝶形节点的距离为N/2
算法的计算复杂度 复乘次数 N N 2 log 2 复乘次数 N N 2 N N 2 log 2 N N 2 log 2 基 2 时间抽取 FFT 算法流图 x[0] x[4] x[2] x[6] X[0] X[2] X[1] X[3] −1 −1 −1 −1 0 W8 0 W8 0 W8 x[1] x[5] x[3] x[7] X[0] X[2] X[1] X[3] −1 −1 −1 −1 0 W8 0 W8 0 W8 1 W8 0 W8 3 W8 2 W8 2 W8 2 W8 −1 −1 −1 −1 第一级 第二级 第三级 FFT 算法流图旋转因子 P WN 规律 第一级的蝶形系数均为 0 WN ,蝶形节点的距离为 1。 第二级的蝶形系数为 0 / 4 , N WN WN ,蝶形节点的距离为 2。 第三级的蝶形系数为 0 /8 2 /8 3 /8 , , , N N N N N WN WN W W ,蝶形节点的距离为 4。 第 M 级 的蝶形系数为 0 1 ( / 2 1) , , , N − WN WN WN ,蝶形节点的距离为 N /2
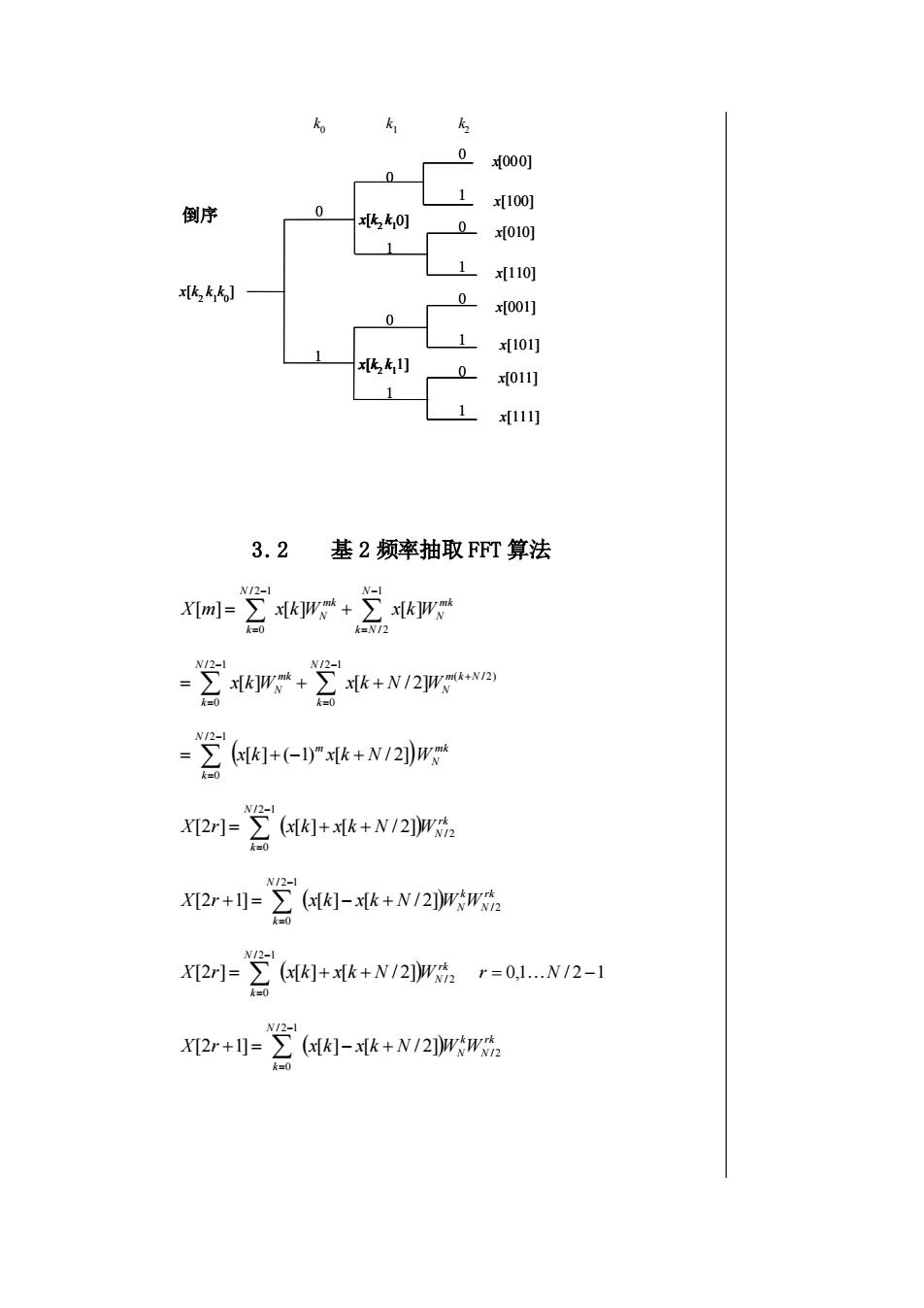
kikok20x[000]1x[100]0倒序x[k, k,0]0x[010]11x[110]x[k,k,k]0x[001]01x[101]x[5k,1]0x[011]1[111]3.2基 2频率抽取FFT算法N/2-1N-12x[kjw+2x[kjWmkX[m]=.0k=N12N/2-1N/2-1x[k + N /2]Wm(+N/2)x[kW*+72=k=oNI2-Wi([K]+(-1)"x[k+ N /2])wmk1N/21WiX[2r]=(x[k]+x[k+ N /2])W/2N/2X[2r +1]=Z([k]-x[k+N /2)wwn/2N/2-1WIX[2r]=(x[]+x[k+ N /2])Wt2r=0,1...N/2-1N/2-1N(x[k]-x[k+ N /2])wwrkX[2r +1]=N/2k=0
倒序 k 0 k 1 k 2 x[k 2 k 1k 0 x[k ] 2 k 1k 0] x[000] x[100] x[010] 0 1 0 1 1] 2 1 x[k k x[k 0] 2 k1 0 1 1] 2 1 x[k k 1] 2 1 x[k k 2 1 x[k k x[k 0] 2 k1 x[k 0] 2 k1 x[k2 k1 0 1 x[110] x[001] x[101] x[011] x[111] 0 1 0 1 0 1 0 1 3.2 基 2 频率抽取 FFT 算法 mk N N k N mk N N k X[m] x[k]W x[k]W 1 / 2 / 2 1 0 − = − = = + ( / 2) / 2 1 0 / 2 1 0 [ ] [ / 2] m k N N N k mk N N k x k W x k N W + − = − = = + + ( ) mk N m N k x[k] ( 1) x[k N / 2] W / 2 1 0 = + − + − = ( ) rk N N k X r x k x k N W / 2 / 2 1 0 [2 ] = [ ]+ [ + / 2] − = ( ) rk N k N N k X r x k x k N W W / 2 / 2 1 0 [2 +1] = [ ]− [ + / 2] − = ( ) rk N N k X r x k x k N W / 2 / 2 1 0 [2 ] = [ ]+ [ + / 2] − = r = 0,1N / 2 −1 ( ) rk N k N N k X r x k x k N W W / 2 / 2 1 0 [2 +1] = [ ]− [ + / 2] − =