《数字信号处理》课程教学资源（教案讲义）ch2 离散傅立叶变换

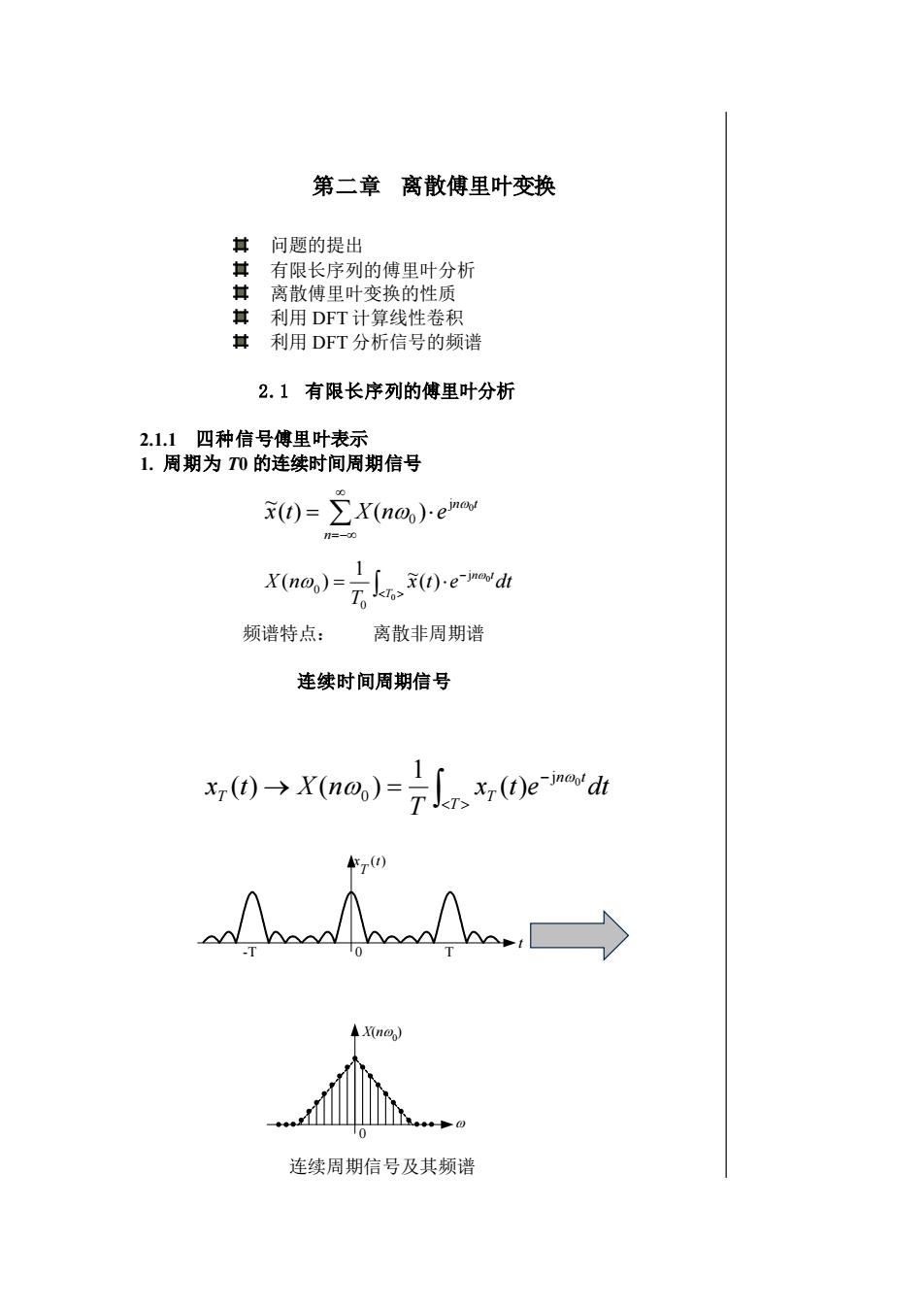
第二章离散傅里叶变换#问题的提出#有限长序列的傅里叶分析#离散傅里叶变换的性质共利用DFT计算线性卷积其利用DFT分析信号的频谱2.1有限长序列的傅里叶分析2.1.1四种信号傅里叶表示1.周期为TO的连续时间周期信号EX(noo)eimorx(t) =1=-00x(t)-e-jnoo'dtX(no)=T, Jk>频谱特点：离散非周期谱连续时间周期信号X (t)e-jnl dtx(t) → X(no)xr(0)AX(no)连续周期信号及其频谱

第二章 离散傅里叶变换 问题的提出 有限长序列的傅里叶分析 离散傅里叶变换的性质 利用 DFT 计算线性卷积 利用 DFT 分析信号的频谱 2.1 有限长序列的傅里叶分析 2.1.1 四种信号傅里叶表示 1. 周期为 T0 的连续时间周期信号 频谱特点： 离散非周期谱 连续时间周期信号 连续周期信号及其频谱 x t e dt T X n n t T 0 0 j 0 0 ( ) 1 ~ ( )   −   =     =− =  n n t x t X n e 0 j 0 ( ) ( ) ~     − → = T n t T xT t e dt T x t X n 0 j 0 ( ) 1 ( ) ( )   t 0 (t) T x -T T  X(n0 ) 0

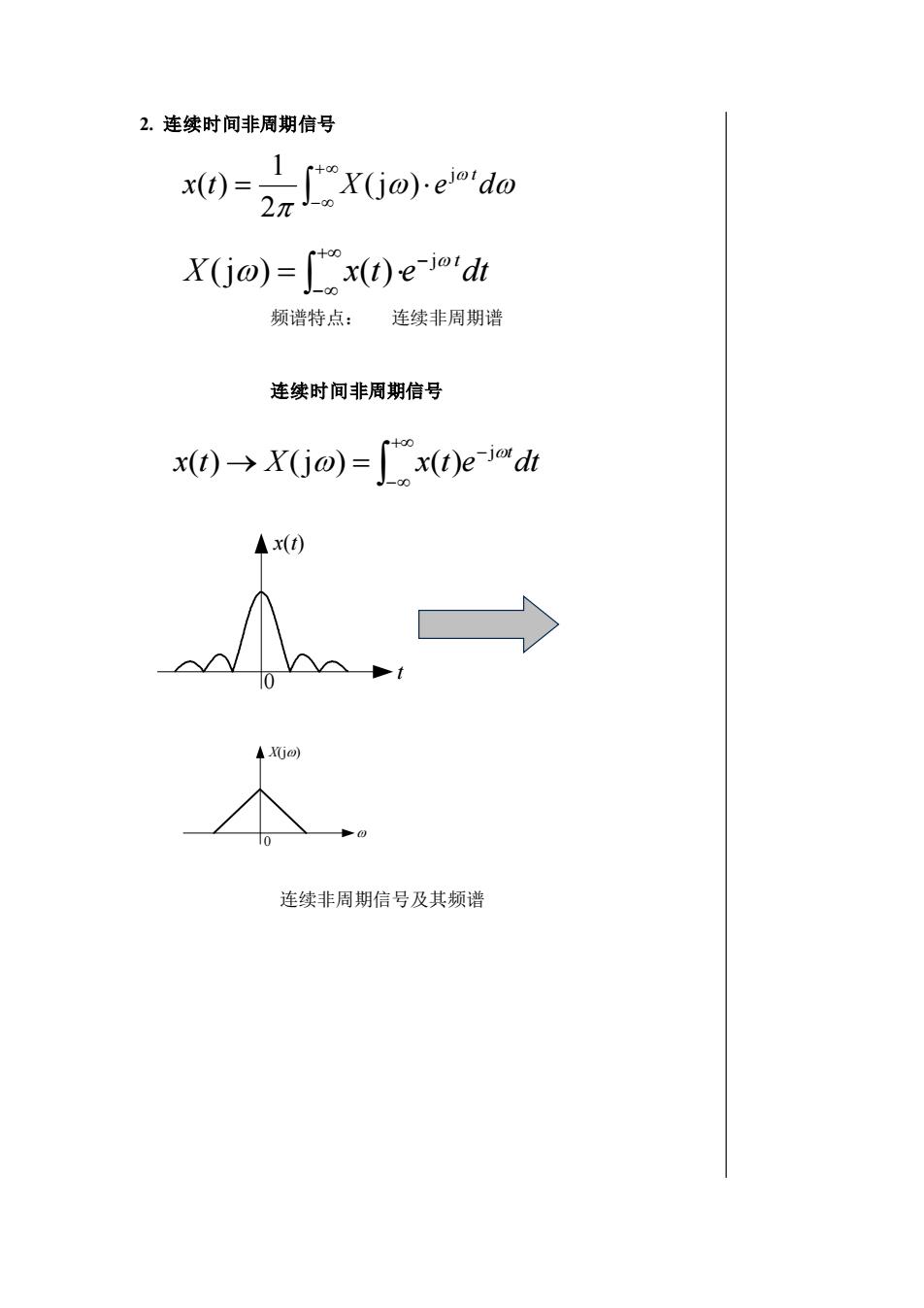
2.连续时间非周期信号(t"x(jo)·ejot dox(t) =w2元X(jo) = [t x(t)e-joidt频谱特点：连续非周期谱连续时间非周期信号x(t) → X(jo) = fx(t)e-jo dtA x(t)04 X(jo)连续非周期信号及其频谱

2. 连续时间非周期信号 频谱特点： 连续非周期谱 连续时间非周期信号 连续非周期信号及其频谱 X x t e dt j t (j ) ( )   − + − =      x t X e d j t (j ) 2 1 ( ) =   + −  + − − x t → X = x t e dt t  j ( ) (j ) ( ) t x(t) 0  X(j) 0

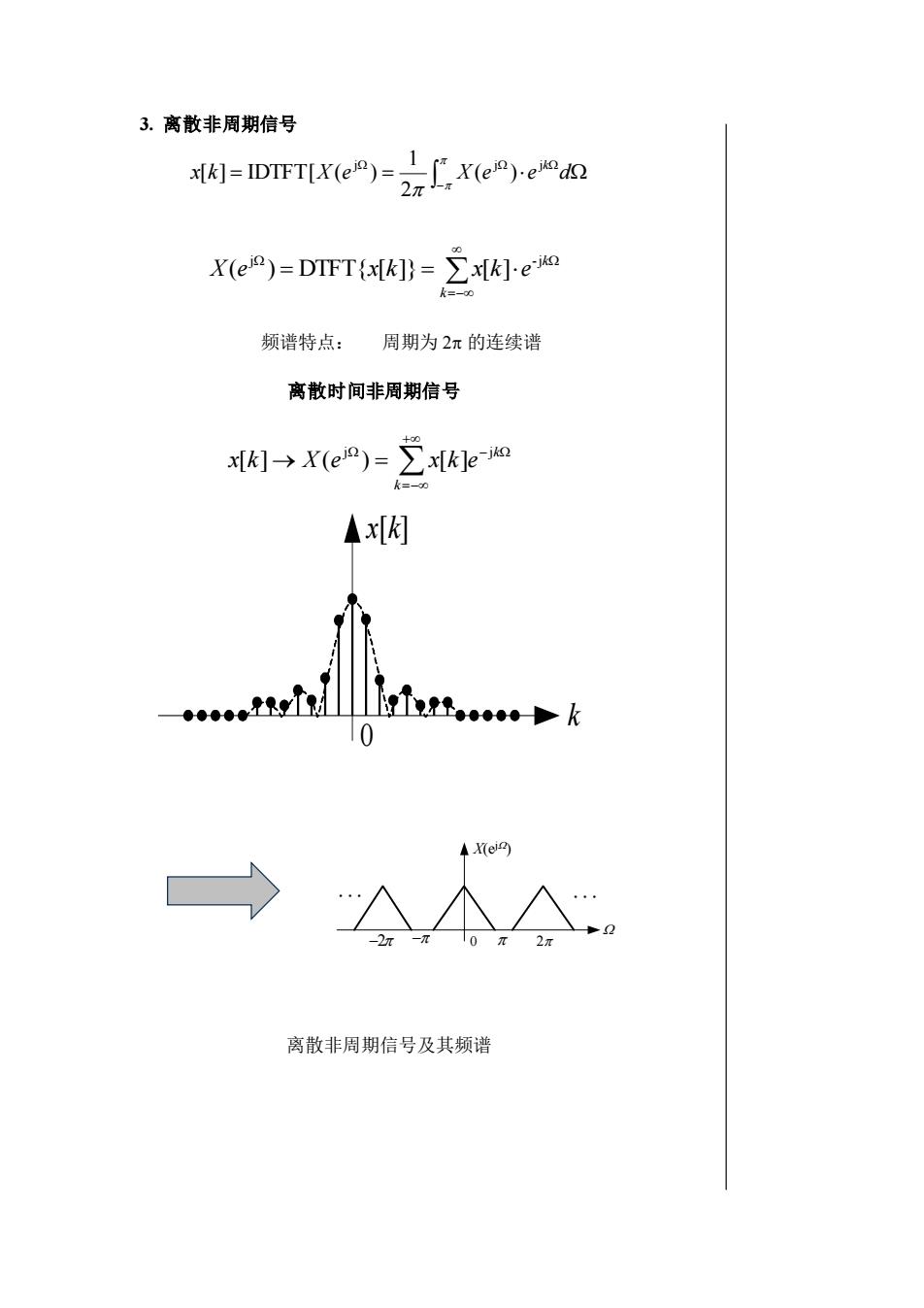
3.离散非周期信号[K] = IDTFT[X(ein)=_[, X(ein),eik dQX(ei9)= DTFT(x[k]) = Zx[k]-e-ik0k=-α频谱特点：周期为2元的连续谱离散时间非周期信号[K]-→ X(ein)= x[k]le-jkA x[K]1eR104X(eid)-2元一元10元2元离散非周期信号及其频谱

3. 离散非周期信号 频谱特点： 周期为 2 的连续谱 离散时间非周期信号 离散非周期信号及其频谱   =−  = =   k k X e x k x k e j -j ( ) DTFT{ [ ]} [ ] = =    −    x k X e X e e d j j jk ( ) 2 1 [ ] IDTFT[ ( )     + =−  −  → = k k x k X e x k e j j [ ] ( ) [ ] k x[k] 0  X(ej ) 0 . . −2 −  2

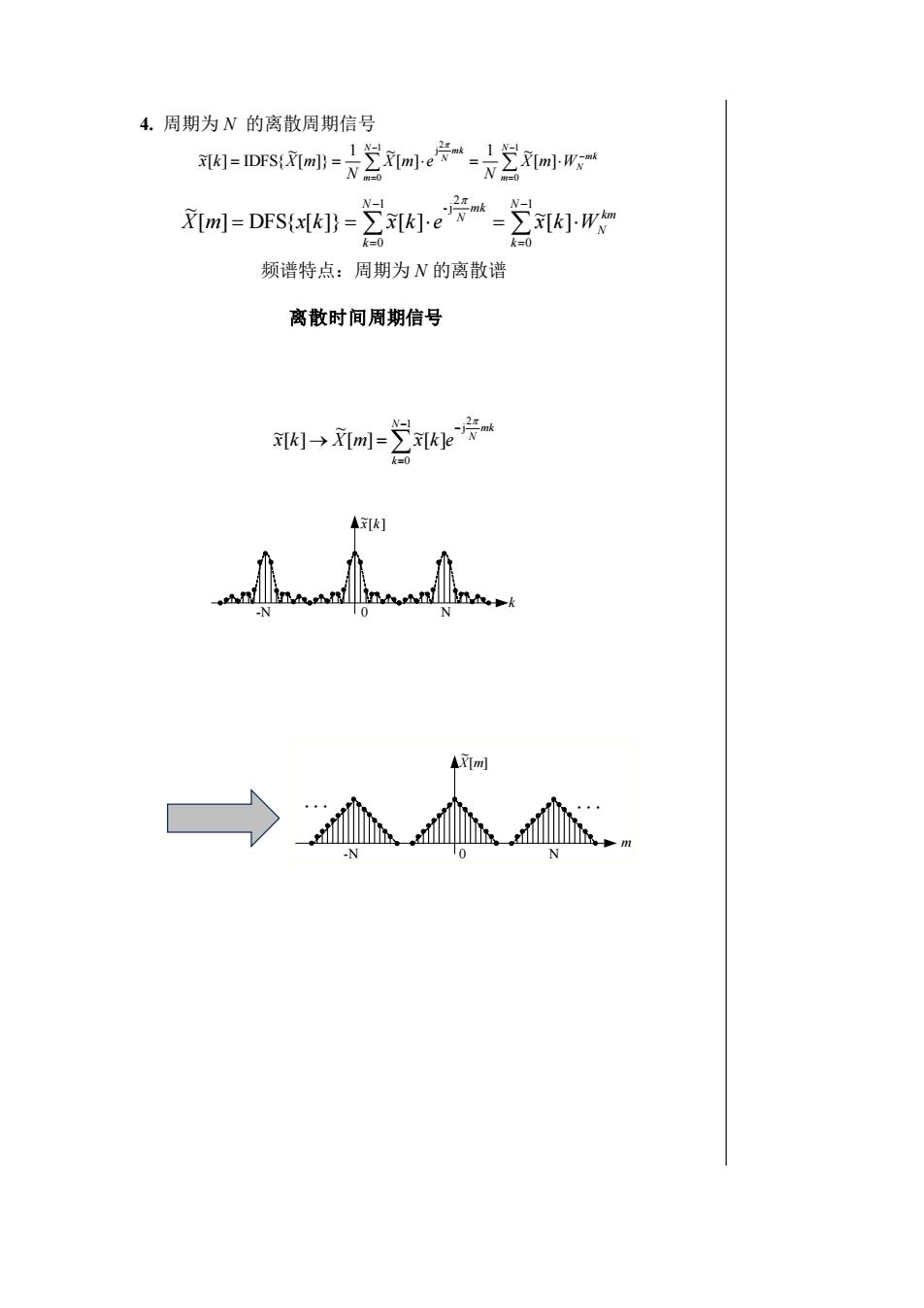
4.周期为N的离散周期信号Xm-ex2mk2X[m]-Wmx[K]=IDFS(X[m]]=NNL-j2mkN-1N1Z[k]-wkmX[m]=DFS(x[k]}=)Z[]e"一Nk=0k=0频谱特点：周期为N的离散谱离散时间周期信号2元mx[k]-→X[m]=x[k]ek=0x[k]-N-NAi[m]-NN

4. 周期为 N 的离散周期信号 频谱特点：周期为 N 的离散谱 离散时间周期信号  − = − → = 1 0 2 j [ ] ~ [ ] ~ [ ] ~ N k mk N x k X m x k e  km N N k mk N N k X m = x k = x k e = x k W − = − = 1 0 2 -j 1 0 [ ] ~ [ ] ~ [ ] DFS{ [ ]} ~  mk N N m mk N N m X m W N X m e N x k X m − − = − = = =   =   1 0 2 j 1 0 [ ] 1 ~ [ ] 1 ~ [ ]} ~ [ ] IDFS{ ~  0 [ ] ~x k k -N N m [ ] ~ X m -N 0 N .

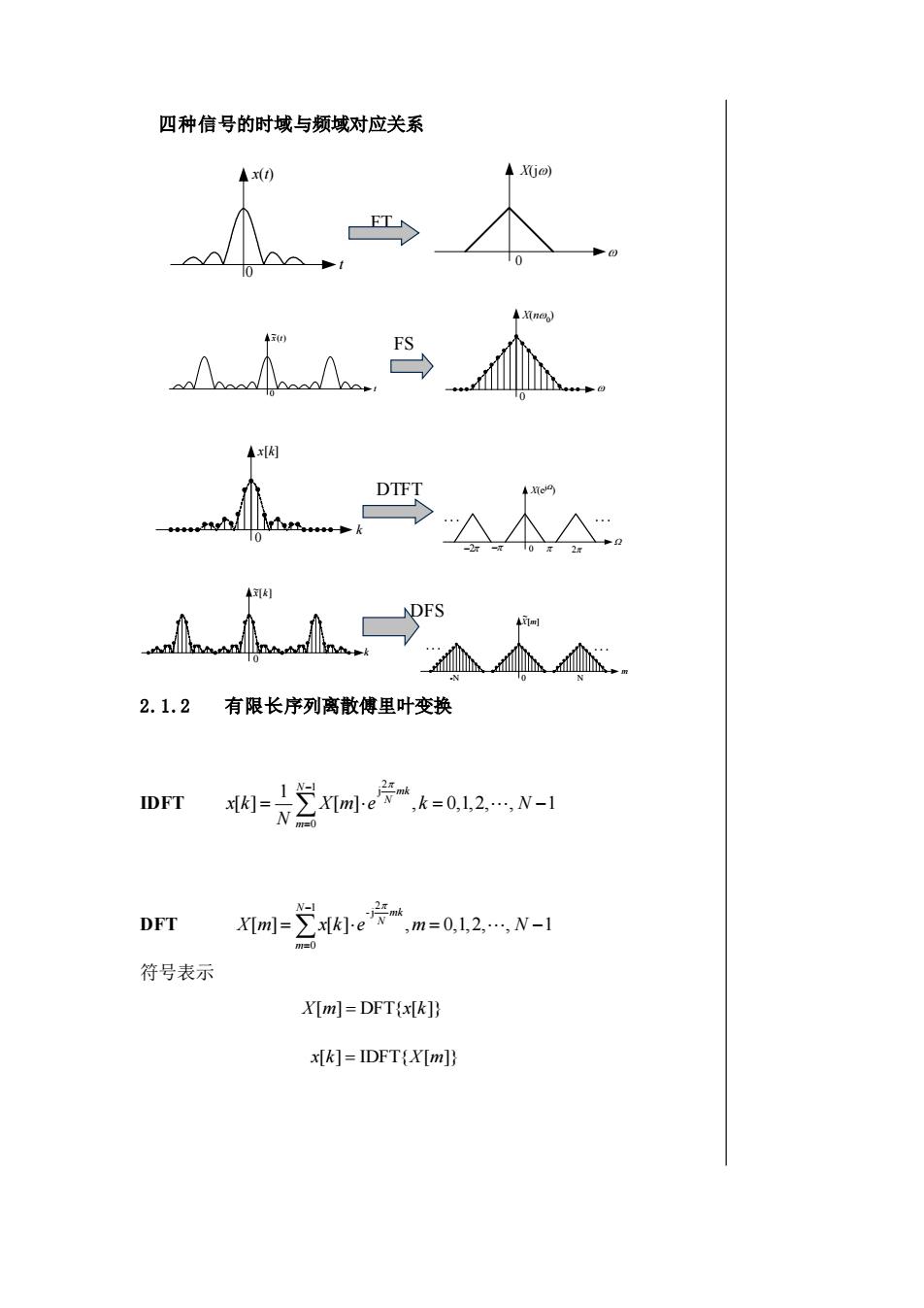
四种信号的时域与频域对应关系 X(jo)4x(t)1X(ng))FS4x[]DTFT(ein)电4[K]NDFS4X[m]Sa2.1.2有限长序列离散傅里叶变换2元mkN-I1IDFTx[k] =X[m]-e'N,k=0,1,2..,N-1NON-I2zmkZx[k]-eDFTX[m]=,m=0,1,2,..,N-1m0符号表示X[m]= DFT(x[k])x[K] = IDFT(X[m]]

四种信号的时域与频域对应关系 FT FS DTFT DFS 2.1.2 有限长序列离散傅里叶变换 IDFT [ ] , 0,1,2, , 1 1 [ ] 2 j 1 0 =   = − − = X m e k N N x k mk N N m   DFT [ ] [ ] , 0,1,2, , 1 2 -j 1 0 =   = − − = X m x k e m N mk N N m   符号表示 X[m] = DFT{x[k]} x[k] = IDFT{X[m]} t x(t) 0  X(j) 0 t 0 ( ) ~x t  X(n0 ) 0 k x[k] 0  X(ej ) 0 . . −2 −  2 0 [ ] ~x k k m [ ] ~X m -N 0 N .