
第2章信号的频域分析任一信号可以在时域对其进行分析和描述,利用傅立叶变换理论也可以对其进行频域分析,以便更好地对信号进行存储、传输和处理,达到提取有用信号的目的信号可分为四大类,与之对应存在四种类型的傅立叶变换,成为信号频谱分机的基础。归纳如下表:信号类型频谱特性变换名称变换公式连续周期CTFSxerd非周期离X(k2) =T散CTFT连续非周期非周期连X(j2)= x(0)e- dt续DFS周期离散离散周期N-lX(k)=x(n)e-"n=0离散非周期DTFT周期连续Zx(n)e-jonX(eja)=(w=2m)四种信号的变化规律为:周期信号的频谱是离散的、互为谐波关系的;非周期信号的频谱是连续的;离散信号的频谱是为周期的;连续信号的频谱是非周期的。所谓信号的频谱分析就是利用傅立叶变换的分析方法,找出与信号时域波形对应的频谱函数的幅度、相位以及能量或功率的分布规律等,以便在频域提取信号的特征实际工程中,通过积分公式求取复杂信号的频谱函数本身就比较困难,何况在许多情况下只是记录了实际信号的一段波形或数据,而没有对应的解析表达式。若对这些信号进行频谱分析,就必须利用离散傅里叶变换(DFT)。DFT表征一个在时域为N点有限长的序列x(n)经过傅里叶变换到频域成为另一个N点有限长序列
第 2 章 信号的频域分析 任一信号可以在时域对其进行分析和描述,利用傅立叶变换理论也可以对其进 行频域分析,以便更好地对信号进行存储、传输和处理,达到提取有用信号的目的。 信号可分为四大类,与之对应存在四种类型的傅立叶变换,成为信号频谱分析 的基础。归纳如下表: 信号类型 变换名称 变换公式 频谱特性 连续周期 CTFS − − = 2 2 ( ) 1 ( ) T T jk t x t e dt T X k 非周期离 散 连续非周期 CTFT X j x t e dt j t − − ( ) = ( ) 非周期连 续 离散周期 DFS − = − = 1 0 2 ( ) ~ ( ) . ~ N n kn N j X k x n e 周期离散 离散非周期 DTFT =− − = n j j n X e x n e ( ) ( ) 周期连续 (ω0=2π) 四种信号的变化规律为:周期信号的频谱是离散的、互为谐波关系的;非周期 信号的频谱是连续的;离散信号的频谱是为周期的;连续信号的频谱是非周期的。 所谓信号的频谱分析就是利用傅立叶变换的分析方法,找出与信号时域波形对应的 频谱函数的幅度、相位以及能量或功率的分布规律等,以便在频域提取信号的特征。 实际工程中,通过积分公式求取复杂信号的频谱函数本身就比较困难,何况在 许多情况下只是记录了实际信号的一段波形或数据,而没有对应的解析表达式。若 对这些信号进行频谱分析,就必须利用离散傅里叶变换(DFT)。DFT 表征一个在 时域为 N 点有限长的序列 x(n) 经过傅里叶变换到频域成为另一个 N 点有限长序列

X(k),即:mN-X(k)=x(n)whx(n)e1=0n=0离散傅里叶反变换(IDFT)定义为12x(k)e*Ex(k)wx(n) =NKON=可见,由于DFT变换对在时域、频域都是离散的,可以通过计算机实现数值计算。而且DFT存在快速算法FFT,可以高速、高效地完成DFT运算。Matlab中提供了相应函数以实现DFT变换对的计算,调用格式为:X=ff(x)其按照基2时间抽取快速算法计算序列x(n)的傅里叶变换,当x(n)的长度为2的整数次幂或者x(n)为实序列时,计算的时间会大大缩短。X=fft(x,n)其是补零或截短的n点傅里叶变换,当x(n)的长度小于n时,在x(n)的尾部补零使x(n)的长度达到n点;当x(n)的长度大于n时,将x(n)截短使x(n)的长度成n点;然后对补零或截短的数据进行快速傅里叶变换。x=ifft(X)和x=ifft(X,n)为相应的反变换。fftshift(x)将fft计算输出的零频移到输出的中心。DFT解决了用计算机对各类信号进行频谱分析的问题,因此可以使用DFT对连续信号进行频谱分析。但必须要对连续信号进行离散化,并且当信号长度为无限长时需要作截短处理。恰当地确定取样时间间隔T和相应的时间长度L,是决定DFT结果是否符合实际的关键因素。如果不满足取样定理的约束条件,在时域欠取样的情况下,会出现频谱混叠而无法恢复原信号频谱,因而不能从时域取样点准确地重建原连续时间信号:如果截断和选取的长度不合适,造成频谱扩散使信号的能量和功率产生泄漏
X (k),即 : − = − = 1 0 2 ( ) ( ) N n kn N j X k x n e = − = 1 0 ( ) N n kn n wN x 离散傅里叶反变换(IDFT)定义为 − = = 1 0 2 ( ) 1 ( ) N k kn N j X k e N x n − = − = 1 0 ( ) 1 N k kn wN X k N 可见,由于 DFT 变换对在时域、频域都是离散的,可以通过计算机实现数值 计算。而且 DFT 存在快速算法 FFT,可以高速、高效地完成 DFT 运算。Matlab 中 提供了相应函数以实现 DFT 变换对的计算,调用格式为: X=fft(x) 其按照基 2 时间抽取快速算法计算序列 x(n)的傅里叶变换,当 x (n) 的长度为 2 的整数次幂或者 x(n)为实序列时,计算的时间会大大缩短。 X=fft(x,n) 其是补零或截短的 n 点傅里叶变换,当 x(n)的长度小于 n 时,在 x(n)的尾部补零使 x(n)的长度达到 n 点;当 x(n)的长度大于 n 时,将 x(n)截短使 x(n)的长度成 n 点; 然后对补零或截短的数据进行快速傅里叶变换。 x=ifft(X)和 x=ifft(X,n)为相应的反变换。 fftshift(x)将 fft 计算输出的零频移到输出的中心。 DFT 解决了用计算机对各类信号进行频谱分析的问题,因此可以使用 DFT 对 连续信号进行频谱分析。但必须要对连续信号进行离散化,并且当信号长度为无限 长时需要作截短处理。恰当地确定取样时间间隔 T 和相应的时间长度 L,是决定 DFT 结果是否符合实际的关键因素。如果不满足取样定理的约束条件,在时域欠 取样的情况下,会出现频谱混叠而无法恢复原信号频谱,因而不能从时域取样点准 确地重建原连续时间信号;如果截断和选取的长度不合适,造成频谱扩散使信号的 能量和功率产生泄漏

利用DFT分析各类信号的频谱时,参数的选择主要满足时域抽样定理、频域来样定理,依据信号时频域能量分布情况,恰当地选择时域取样间隔T和取样长度1当信号的频带宽度无限或很宽,则取频域能量集中在95%--98%的频带宽度。要在频域计算信号的能量,选取fm(信号的最高截频),即选择时域取样间隔T:在时域计算信号的能量,则可选取窗函数,对时间信号进行截短,即选择时间长度L。2.1利用DFT分析连续信号频谱首先调用Matlab的fourier(x,t,w)函数可以在理论上求连续时间信号的频谱例1:求出下列信号的傅立叶幅度谱(1).门函数脉冲信号 xi(t)=(t+0.5)-(t-0.5)(2).高斯信号 x2()=e-12解:(1)利用符号函数求门函数的频谱%符号函数symstwut=sym(Heaviside(t+0.5)-Heaviside(t-0.5));Fw=fourier(ut,t,w);FFw=maple(convert,Fw,'piecewise);FFP=abs(FFw);ezplot(FFP,[-10*pi 10*pi)axis([-10*pi 10*pi 0 1))DC1100.90.80.70.6D.S0.40.30.2D
利用 DFT 分析各类信号的频谱时,参数的选择主要满足时域抽样定理、频域采 样定理,依据信号时频域能量分布情况,恰当地选择时域取样间隔 T 和取样长度 L。 当信号的频带宽度无限或很宽,则取频域能量集中在 95%-98%的频带宽度。即 要在频域计算信号的能量,选取 fm (信号的最高截频),即选择时域取样间隔 T; 在时域计算信号的能量,则可选取窗函数,对时间信号进行截短,即选择时间长度 L。 2.1 利用 DFT 分析连续信号频谱 首先调用 Matlab 的 fourier(x,t,w)函数可以在理论上求连续时间信号的频谱。 例 1:求出下列信号的傅立叶幅度谱 (1). 门函数脉冲信号 x1(t)=(t+0.5)-(t-0.5) (2). 高斯信号 x2(t)=e 2 −t 解:(1)利用符号函数求门函数的频谱 syms t w %符号函数 ut=sym('Heaviside(t+0.5)-Heaviside(t-0.5)'); Fw=fourier(ut,t,w); FFw=maple('convert',Fw,'piecewise'); FFP=abs(FFw); ezplot(FFP,[-10*pi 10*pi]) axis([-10*pi 10*pi 0 1])
(2)利用符号函数求高斯函数的频谱symswtft=exp(-t.^2);fw=fourier(ft,t,w);ezplot(fw)1/2exp(-1/4w2)1.81.61.41.20.80.60:40.22.1.1连续周期信号的频谱分析应用离散傅里叶变换DFT,分析连续周期信号xr(t)的频谱。连续周期信号在满足一定条件下,可以通过傅立叶级数(CTFS)展开为一系列正弦信号的线性叠加,其频谱函数X(kQ)是离散频率的复函数,因而周期信号的频谱结构具有离散性和谐波性。-X(k2) =对x(t)以T为间隔进行取样,长度为一个周期T,dt→T,『→Z,x(t)→x(n),To=NT,得到1 N-!Ex(n)e-ikonT TX(k2)=T.2
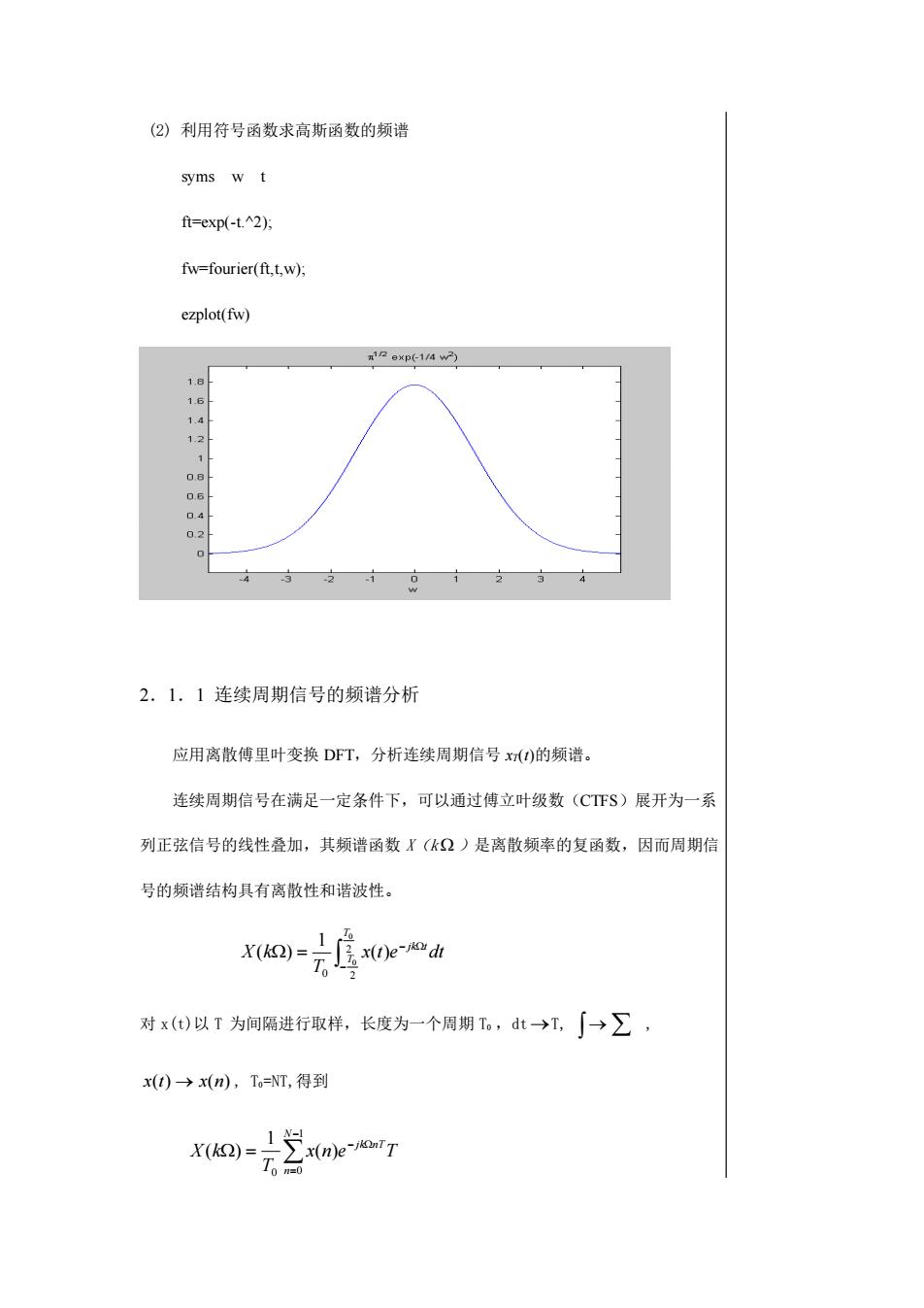
(2) 利用符号函数求高斯函数的频谱 syms w t ft=exp(-t.^2); fw=fourier(ft,t,w); ezplot(fw) 2.1.1 连续周期信号的频谱分析 应用离散傅里叶变换 DFT,分析连续周期信号 xT(t)的频谱。 连续周期信号在满足一定条件下,可以通过傅立叶级数(CTFS)展开为一系 列正弦信号的线性叠加,其频谱函数 X(k )是离散频率的复函数,因而周期信 号的频谱结构具有离散性和谐波性。 − − = 2 0 2 0 0 ( ) 1 ( ) T T jk t x t e dt T X k 对 x(t)以 T 为间隔进行取样,长度为一个周期 T0 ,dt → T, → , x(t) → x(n) , T0=NT,得到 x n e T T X k N n jk nT − = − = 1 0 0 ( ) 1 ( )

THx(n)eTo =o1_X(k)N连续周期信号的频谱求解步骤:(1)根据取样定理,确定时域取样间隔T;(2)计算一个周期内的取样点数N。使用FFT命令作N点FFT计算,求得X(K);(3)1(4)最后求得连续周期信号的频谱为X(k2)=X(k)N例2:已知一个连续周期信号x(t)=1-cos(πt)+2sin(2πt)+cos(3πt),用DFT计算其频谱。解:信号基频Q=元,周期To=2;最高次谐频为3Q=3元,所以N≥7。可取N=8,16,32,64,..进行比较。T0=2;N=16:T=TO/N;周期为TO,FFT的点数为N,时域取样间隔为TX=1/N*ft(x,N);用FFT计算其频谱,其结果为:T0=2; N=16;T=T0/N;t=O:T:TO;x=1-cos(pi*t)+2*sin(2*pi*t)+cos(3*pi*t);X=1/N*ft(x,N);f=1/T/N*(-N/2:(N/2-1);%N,f=1/T/N*(-(N-1)/2:(N-1)/2);subplot(2,1,1);stem(f,abs(fftshif(X);xlabel(Frequency(Hz));ylabel('magnitude')subplot(2,1,2);stem(f,angle(fftshif(X);xlabel(Frequency(Hz)");ylabel('phase');
= − = − 1 0 2 0 ( ) N n kn N j x n e T T = ( ) 1 X k N 连续周期信号的频谱求解步骤: (1) 根据取样定理,确定时域取样间隔 T; (2) 计算一个周期内的取样点数 N。 (3) 使用 FFT 命令作 N 点 FFT 计算,求得 X (k); (4) 最后求得连续周期信号的频谱为 X (k )= N 1 X (k) 例 2: 已知一个连续周期信号 x (t) = 1 – cos (πt) + 2sin (2πt) + cos (3πt), 用 DFT 计算其频谱。 解: 信号基频 =π,周期 T0=2;最高次谐频为 3 =3π,所以 N≥7。 可取 N=8,16,32,64,.进行比较。 T0=2;N=16;T=T0/N; 周期为 T0,FFT 的点数为 N,时域取样间隔为 T: X = 1 / N * fft (x , N); 用 FFT 计算其频谱,其结果为: T0=2; N=16;T=T0/N; t=0:T:T0; x=1-cos(pi*t)+2*sin(2*pi*t)+cos(3*pi*t); X=1/N*fft(x,N); f=1/T/N*(-N/2:(N/2-1));%N,f=1/T/N*(-(N-1)/2:(N-1)/2); subplot(2,1,1);stem(f,abs(fftshift(X))); xlabel('Frequency(Hz)');ylabel('magnitude'); subplot(2,1,2);stem(f,angle(fftshift(X))); xlabel('Frequency(Hz)');ylabel('phase');