《数字信号处理》课程教学资源（教案讲义）ch5 FIR数字滤波器的设计

第5章FIR数字滤波器的设计5. 1线性相位FIR滤波器的性质线性相位系统的时域特性线性相位系统的频域特性线性相位系统H(=)的零点分布特性FIR滤波器的定义MH(2)=Z b,=-kk0M阶（长度N=M+1）的FIR数字滤波器[bk=0,]..,Mh[k] =[o其它FIR滤波器的特点1]h[K]在有限范围内非零，系统总是稳定的。2)容易设计成线性相位3)可利用FFT实现4)运算量比IIR大FIR滤波器设计指标AHein)1+0,1-8p过渡带通带阻带Q02p2s严格线性相位定义H(eig) =|H(ein)leje()若(W)=-aW,则称系统H(2)是严格线性相位的。例：单频信号exp(jWOk)通过线性相位(LTI)系统的响应T(e i2ok ) = H(ejgo )lejpo(k-a)20le

第 5 章 FIR 数字滤波器的设计 5.1 线性相位 FIR 滤波器的性质 • 线性相位系统的时域特性 • 线性相位系统的频域特性 • 线性相位系统 H(z)的零点分布特性 FIR 滤波器的定义 k k M k H z b z − = =  0 ( ) M 阶(长度 N=M+1) 的 FIR 数字滤波器 h[k] =    = 0 其它 bk k 0,1,,M FIR 滤波器的特点 1)h[k]在有限范围内非零，系统总是稳定的。 2)容易设计成线性相位 3)可利用 FFT 实现 4)运算量比 IIR 大 FIR 滤波器设计指标 严格线性相位定义 j j j ( ) (e ) (e ) e    =  H H 若 f(W)= - aW, 则称系统 H(z)是严格线性相位的。 例： 单频信号 exp(jW0 k)通过线性相位(LTI)系统的响应 j j j ( ) 0 0 0 {e } (e ) e    − = k k T H 通带 过渡带 阻带   p  s ej   p − p s

广义线性相位定义H(ej)= A(2)e-(a+P)A(W)称为幅度频函数线性相位系统的时域特性V下定理：H(=)=b,=-*为线性相位的充要条件为 h[K]=±h[M-k]=03M=4偶对称M=3偶对称M=4奇对称M=3奇对称线性相位系统的频域特性1)1型：(h[k]-h[M-k],M为偶数)例: M=4, h[K]-[h[0], h[1], h[2], h[1], h[0]H(e/)=h[0](1+e-j4)+h[1](e-/ +e-J32)+ h[2]e-/20=2h[0]e-/2 cos22+2h[]e-/2 cos+[2]e-120A(2) = h[2]+ 2h[2 -1]cos Q2 + 2h[2 -2]cos 2QL=M/22h[L-k]cosk2=Ea[k]coskA(2)= h[]+Zk=(k=2a[k]coskA(-2)= A (2)A(Q+2元)= A(2)A(2元 -Q2)= A(2)A(W)关于0和p点偶对称A(W)关于0和p点偶对称H(ej)=e-jn4cosQ/2

广义线性相位定义 j j( ) (e ) ( )e  −  H = A  A (W)称为幅度频函数 线性相位系统的时域特性 定理： k k M k H z b z − = =  0 ( ) 为线性相位的充要条件为 h[k]=h[M-k] M=4 偶对称 M=3 偶对称 M=4 奇对称 M=3 奇对称 线性相位系统的频域特性 1) 1 型: (h[k]=h[M-k], M 为偶数) 例：M=4 , h[k]={h[0], h[1], h[2], h[1], h[0]}  −  −  −  −  =     4 3 2 ( ) [0](1 ) [1]( ) [2] j j j j j H e h e h e e h e −  −  −  =   2 2 2 2 [0] cos 2 2 [1] cos [2] j j j h e h e h e A() = h[2] 2h[2 −1]cos  2h[2 − 2]cos 2 L = M / 2  =  −  =   = = A h L h L k k a k k L k L k ( ) [ ] 2 [ ]cos [ ]cos 1 0  =   = A a k k L k ( ) [ ]cos 0 A(  2π) = A() A(−) = A () A(2 −) = A() A (W)关于 0 和 p 点偶对称 A (W)关于 0 和 p 点偶对称 (e ) e 4cos / 2 j j 2 =   −  H 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4

A(2)2元元02)II 型:(h[K]=h[M-k]),M 为奇数M=3 h[K]={h[0], h[1], h[1], h[0]]H(ej°)= h[0](1+e-j32)+ h[1](e-jn +e-j22)=2h[0]e-159 cos(1.52)+2h[1]e-1.50 cos0.5A(2)=2h[1]cos(0.52)+2h[0]cos(1.5)cos(0.52）的周期=4元cos(1.52）的周期=(4/3)元A（2）的周期=4元A(2)=2h[1|cos(0.52)+2h[0|cos(1.52)A() =2h[1-0]cos[(0+0.5)]+2h[1-1]cos(1+0.5))记：(M-1)/2=LA4(2)=2h[L-k]cos[(k +0.5)2]K=0b[k]cos[(k +1/2)]k=0A(p)=0不能用于高通、带阻滤波器的设计A(2元-2)=b[k]cos[(k +1/2)(2元-2)]k0Kb[k]cos(2元k+元-2(k+1/2))k=0H(W)关于W=p点奇对称例: h[K]=(d [K]+d [k-1]2

 2  4 0 A()  2  4 0 A()  2  4 0 A() 2) II 型:( h[k]=h[M-k]), M 为奇数 M=3 h[k]={h[0], h[1], h[1], h[0]} ( ) [0](1 ) [1]( )  − 3 −  − 2 =    j j j j H e h e h e e =    −  −  2 [0] cos(1.5 ) 2 [1] cos0.5 j1.5 j1.5 h e h e A() = 2h[1]cos(0.5)  2h[0]cos(1.5) cos(0.5  ) 的周期=4  cos(1.5  ) 的周期=(4/3)  A (  ) 的周期=4  A() = 2h[1]cos(0.5)  2h[0]cos(1.5) A() = 2h[1− 0]cos[(0  0.5)] 2h[1−1]cos((1 0.5)) 记：(M −1)/ 2 = L ( ) 2 [ ]cos[( 0.5) ] 0  =  −   = A h L k k L k [ ]cos[( 1/ 2) ] 0 =    = b k k L k A (p )= 0 不能用于高通、带阻滤波器的设计 (2 ) [ ]cos[( 1/ 2)(2 )] 0 − =   − = A  b k k  L k [ ]cos(2 ( 1/ 2) ) 0 =   −  = b k k k L k   H (W)关于 W =p 点奇对称 例：h[k]=(d [k]+d [k-1])/2

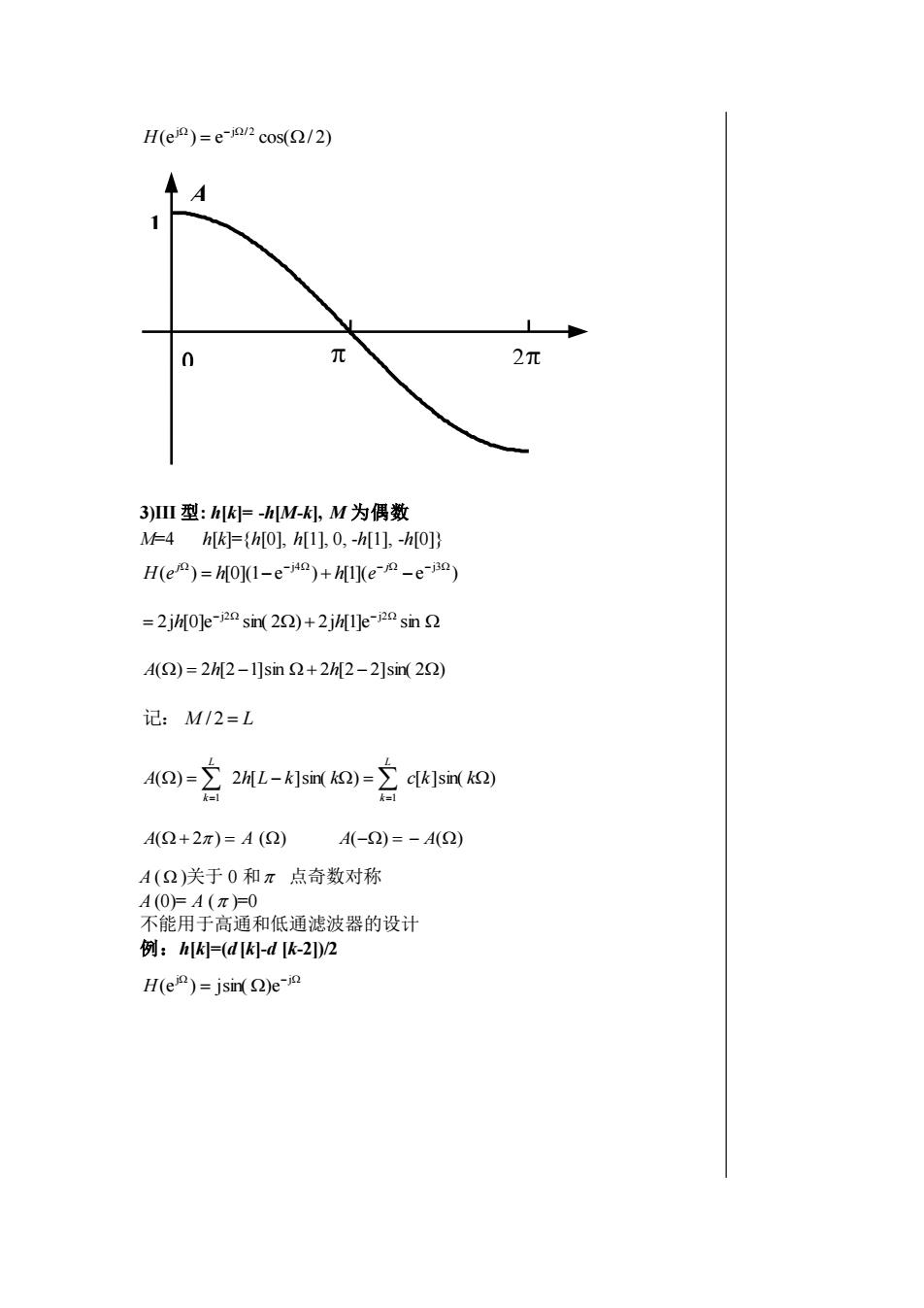
H(ejg)=e-jin/2 cos(2/2)AA1元2元03]III型：h[k]=-h[M-k],M为偶数M=4h[k]={h[0], h[1], 0, -h[1], -h[0]]H(ej9)= h[0](1-e-j4)+ h[1](e-j0 -e-j32)= 2jh[0]e-j22 sin(292) +2jh[1]e-j2° sin 2A(2) = 2h[2-1]sin 2+2h[2 -2]sin(22)记：M/2=L222A(2) = 2h[L-k]sin( k2)=c[k]sin( k)1k=1A(2+2元)= A (2)A(-2)= - A(Q2)A(Q)关于0和元点奇数对称A(0)=A(元)=0不能用于高通和低通滤波器的设计例: h[K]-(d [k]-d [k-2])/2H(ej)= jsin(2)e-jn

(e ) e cos( / 2) j j / 2 =   −  H 3)III 型: h[k]= -h[M-k], M 为偶数 M=4 h[k]={h[0], h[1], 0, -h[1], -h[0]} ( ) [0](1 e ) [1]( e )  − j4 −  − j3 = −  − j j H e h h e =    −  −  2j [0]e sin( 2 ) 2j [1]e sin j2 j2 h h A() = 2h[2 −1]sin   2h[2 − 2]sin( 2) 记： M / 2 = L ( ) 2 [ ]sin( ) [ ]sin( ) 1 1  =  −  =   = = A h L k k c k k L k L k A(  2 ) = A () A(−) = − A() A (  )关于 0 和  点奇数对称 A (0)= A (  )=0 不能用于高通和低通滤波器的设计 例：h[k]=(d [k]-d [k-2])/2  −  =  j j H(e ) jsin( )e 0 1   A ()

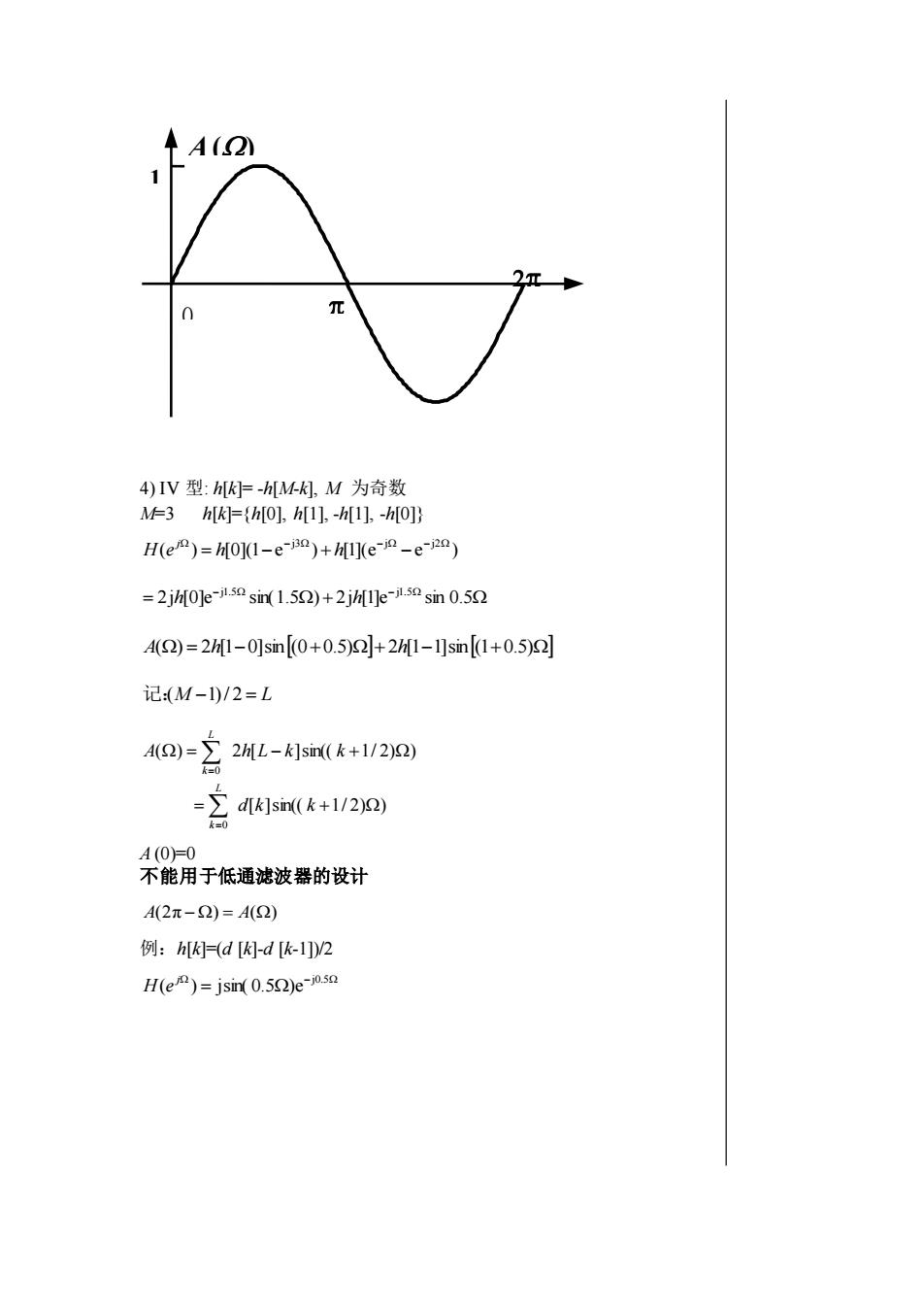
1(2)22元04)IV型:h[Kk]=-h[M-k],M为奇数M=3 h[k]=(h[0], h[1], -h[1], -h[0]]H(ej9)= h[0](1-e-j3)+h[1](e-j2 -e-j22)=2jh[0]e-j1.50 sin(1.52)+2jh[]e-i1.50 sin 0.5A(2)=2h[1-0]sin [(0+0.5)]+2h[1-1]sin[(1+0.5)2记:(M-1)/2=LA(2)=2 2h)[L-klsi(k+1/2)2)K0-2.d[k]sin(k +1/2)2)k=0A (0)=0不能用于低通滤波器的设计A(2元-2)=A(Q)例: h[K]-(d [K]-d [k-1]/2H(e/°)= jsin( 0.52)e-j0.50

4) IV 型: h[k]= -h[M-k], M 为奇数 M=3 h[k]={h[0], h[1], -h[1], -h[0]} ( ) [0](1 e ) [1](e e )  − j3 − j − j2 H e = h −  h − j =    −  −  2j [0]e sin(1.5 ) 2j [1]e sin 0.5 j1.5 j1.5 h h A() = 2h[1−0]sin(00.5)2h[1−1]sin(10.5) 记：(M −1)/ 2 = L [ ]sin(( 1/ 2) ) ( ) 2 [ ]sin(( 1/ 2) ) 0 0 =    = −     = = d k k A h L k k L k L k A (0)=0 不能用于低通滤波器的设计 A(2π −) = A() 例：h[k]=(d [k]-d [k-1])/2  −  =  j0.5 ( ) jsin( 0.5 )e j H e 0 A() 1  