
第3章系统分析与设计信息系统就是为了有效的传输和交换信息而对载荷信息的信号进行加工、处理和变换的设备的总称。系统根据输入、输出信号的不同分为连续系统和离散系统。其分析方法有卷积法,零输入、零状态法,变换域法等。3.1连续系统分析3.1.1卷积积分法求解系统的响应对LTI连续系统,输入信号为x(y),输出信号为y(),系统的冲激响应为h(t)则输入、输出之间的关系为:时域:y(t)=x()*h()频域:Y(j@)=X(j)H(jo)其中线性卷积的计算引入了DFT分析连续信号的频谱。例1:图(A)和(B)分别表示一个LTI连续系统的输入x(t)和单位冲激响应h(t),试利用DFT的快速算法计算该系统的零状态响应。+th(t)x(t)(A)(B)134解:T=1/8; Tx=3 ; Mx=Tx/T;Th=4; Mh =Th/T;L=Mh+Mx-1;
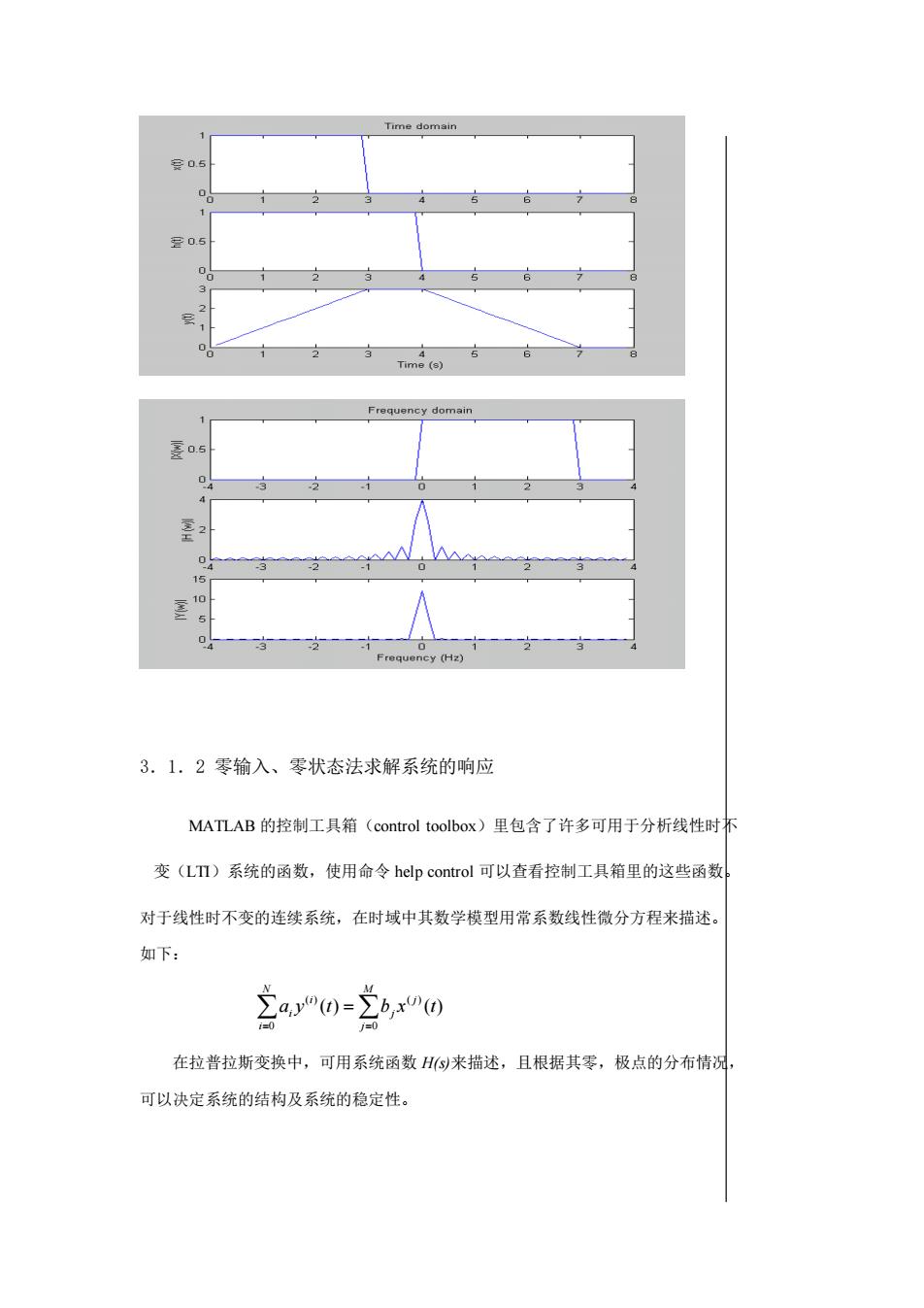
第 3 章 系统分析与设计 信息系统就是为了有效的传输和交换信息而对载荷信息的信号进行加工、处理 和变换的设备的总称。系统根据输入、输出信号的不同分为连续系统和离散系统。 其分析方法有卷积法,零输入、零状态法,变换域法等。 3.1 连续系统分析 3.1.1 卷积积分法求解系统的响应 对 LTI 连续系统,输入信号为 x(t),输出信号为 y(t),系统的冲激响应为 h(t), 则输入、输出之间的关系为: 时域:y(t)=x(t)*h(t) 频域:Y(jω)=X(jω) H(jω) 其中线性卷积的计算引入了 DFT 分析连续信号的频谱。 例 1:图(A)和(B)分别表示一个 LTI 连续系统的输入 x(t)和单位冲激响应 h(t) ,试利用 DFT 的快速算法计算该系统的零状态响应。 x(t) h(t) (A) (B) 1 1 3 4 解: T=1/8; Tx=3 ; Mx=Tx/T; Th=4; Mh =Th/T; L=Mh+Mx-1;

N=64;x=[ones(1,Mx),zeros(1,N -Mx)];h=[ones(1,Mh),zeros(1,N -Mh)];X=T.*fft(x,N);,H=T.*fft(h,N);Y=X.*H;y=1/T.*ift(Y,N);figure(1);t=[0:N-1]*T;subplot(3,1,1); plot(t,x);ylabel(x(t)); title(Time domain');subplot(3,1,2); plot(t,h);ylabel(h(t));subplot(3,1,3); plot(t(2:N), real(y(1:N-1);ylabel(y(t);xlabel(Time (s));figure(2),Fs= 1/T,w-[0:N-1]*Fs/N;subplot(3,1,1); plot(w-Fs/2,fftshift(abs(x),ylabel(X(w)");title("Frequency domain);subplot(3,1,2); plot(w-Fs/2,fftshift(abs(H); ylabel(°H (w)I);subplot(3,1,3); plot(w-Fs/2,fftshift(abs(Y),ylabel(Y(w))xlabel (Frequency (Hz);
N=64; x=[ones(1,Mx),zeros(1,N -Mx)]; h=[ones(1,Mh),zeros(1,N -Mh)]; X=T.*fft(x,N); H=T.*fft(h,N); Y=X.*H; y=1/T.*ifft(Y,N); figure(1); t=[0:N-1]*T; subplot(3,1,1); plot(t,x); ylabel('x(t)'); title('Time domain'); subplot(3,1,2); plot(t,h); ylabel('h(t)'); subplot(3,1,3); plot(t(2:N), real(y(1:N-1))); ylabel('y(t)'); xlabel('Time (s)'); figure(2); Fs= 1/T; w=[0:N-1]*Fs/N; subplot(3,1,1); plot(w-Fs/2,fftshift(abs(x))); ylabel('|X(w)|');title('Frequency domain'); subplot(3,1,2); plot(w-Fs/2,fftshift(abs(H))); ylabel('|H (w)|'); subplot(3,1,3); plot(w-Fs/2,fftshift(abs(Y)));ylabel('|Y(w)|'); xlabel ('Frequency (Hz)');
复0.50.620.5O2O1510LDreguency(Hz)3.1.2零输入、零状态法求解系统的响应MATLAB的控制工具箱(controltoolbox)里包含了许多可用于分析线性时拆变(LT)系统的函数,使用命令helpcontrol可以查看控制工具箱里的这些函数对于线性时不变的连续系统,在时域中其数学模型用常系数线性微分方程来描述。如下:Za,y(t)=)Zb,x((t)i=0j=0在拉普拉斯变换中,可用系统函数H(s)来描述,且根据其零,极点的分布情况可以决定系统的结构及系统的稳定性
3.1.2 零输入、零状态法求解系统的响应 MATLAB 的控制工具箱(control toolbox)里包含了许多可用于分析线性时不 变(LTI)系统的函数,使用命令 help control 可以查看控制工具箱里的这些函数。 对于线性时不变的连续系统,在时域中其数学模型用常系数线性微分方程来描述。 如下: ( ) ( ) ( ) 0 ( ) 0 a y t b x t j M j j i N i i = = = 在拉普拉斯变换中,可用系统函数 H(s)来描述,且根据其零,极点的分布情况, 可以决定系统的结构及系统的稳定性

2bsJ=oH(s) =as'i=0另外还可以用状态变量分析法进行系统描述。此设计完成用Matlab实现几种分析方法的相互转换。在Matlab中,描述系统的传递函数(系统函数)型tf(transferfunction),零极点型zp(zeropole)以及状态变量型ss(statespace)三种方式可以方便的转换Matlab相应的语句为:tf2zp—一系统函数型转换到零极点型tf2ss——系统函数型转换到状态变量型zp2tf——零极点型转换到系统函数型zp2ss——零极点型转换到状态变量型ss2tf—一状态变量型转换到系统函数型Ss2zp——一状态变量型转换到零极点型例2:已知描述LTI系统的数学模型为常系数线性微分方程:y"(t)+8 y"(t)+19 y'(t)+12y(t)=2 f'(t)+10f(t)将其转换为①零,极点型。②状态变量型。解:1 .num=[2,10];den-[1 8 19 12];[z,p,k]=tf2zp(num,den)2. num=[2,10]; den=[181912][a b c dj=tf2ss(num,den)MATLAB提供了用于分析LTI系统的函数,可对微分方程描述的系统的响应进行仿真。使用MATLAB命令可以计算系统的各种时间响应:如单位冲激响应、单位阶跃响应、零输入响应、零状态响应和完全响应。在调用这些函数时,需要用系数向量表示系统。在MATLAB中可使用向量b=[bm,bm-1,.,bi,bo]和向量a-[an,an-]..,al,ao],分别
= = = N i i i M j j j a s b s H s 0 0 ( ) 另外还可以用状态变量分析法进行系统描述。 此设计完成用Matlab 实现几种分析方法的相互转换。 在 Matlab 中,描述系统的传递函数(系统函数)型 tf(transfer function),零极点 型 zp(zero pole)以及状态变量型 ss(state space)三种方式可以方便的转换。 Matlab 相应的语句为: tf2zp——系统函数型转换到零极点型 tf2ss——系统函数型转换到状态变量型 zp2tf——零极点型转换到系统函数型 zp2ss——零极点型转换到状态变量型 ss2tf——状态变量型转换到系统函数型 ss2zp——状态变量型转换到零极点型 例 2:已知描述 LTI 系统的数学模型为常系数线性微分方程: y (t) +8 y (t) +19 y (t) +12y(t)=2 f (t) +10 f ( t ) 将其转换为①零,极点型。②状态变量型。 解: 1 .num=[2,10];den=[1 8 19 12]; [z,p,k]=tf2zp(num,den) 2.num=[2,10];den=[1 8 19 12] [a b c d]=tf2ss(num,den) MATLAB 提供了用于分析 LTI 系统的函数,可对微分方程描述的系统的响应 进行仿真。使用 MATLAB 命令可以计算系统的各种时间响应:如单位冲激响应、 单位阶跃响应、零输入响应、零状态响应和完全响应。 在调用这些函数时,需要用系数向量表示系统。 在 MATLAB 中可使用向量 b=[bm,bm-1,.,b1,b0]和向量 a=[an,an-1,.,a1,a0],分别

为系统函数分子多项式和分母多项式的系数,注意均按s的降幂排列其系数直至s(1)用命令impulse可以求解系统的单位冲激响应:impulse(sys):计算并画出系统的冲激响应,Sys可以是用命令tf、zpk或ss建立的系统函数。impulse(sys,t):计算并画出系统在向量t定义的时间内的冲激响应。Y=impulse(sys,t):向量Y保存对应时间的系统输出值。例3:已知系统的微分方程为y"(t)+5y(t)+6y(t)=2x(t)+8x(t),计算该系统的单位冲激响应。解:b=[2,8];a=[1,5,6];t=0:0.1:10;y=impulse(b,a,t);(2)用命令step求解系统的单位阶跃响应step(sys):计算并画出系统的冲激响应,sys可以是用命令tf、zpk或ss建立的系统函数。step(sys,t):计算并画出系统在向量t定义的时间内的冲激响应。Y=step(sys,t):向量Y保存对应时间的系统输出值。(3):使用命令Isim求解系统在任意输入下的响应Isim(sys,x,t)计算并画出任意输入下系统的零状态响应,sys可以是用命令tf、zpk或ss建立的系统函数,t为时间向量定义时间范围,x为系统的输入。Isim(sys,x,t,zi)计算并画出系统的完全响应,但sys必须是状态空间形式的系统函数,zi为系统的初始状态。Y=lsim(sys,x,t,zi):向量Y保存对应时间的系统输出值。b-[2,8];a-[1,5,6]sys=tf(b,a);
为系统函数分子多项式和分母多项式的系数,注意均按 s 的降幂排列其系数直至 s 0。 (1) 用命令 impulse 可以求解系统的单位冲激响应: impulse(sys):计算并画出系统的冲激响应,sys 可以是用命令 tf、zpk 或 ss 建 立的系统函数。 impulse(sys, t):计算并画出系统在向量 t 定义的时间内的冲激响应。 Y=impulse(sys, t):向量 Y 保存对应时间的系统输出值。 例 3: 已知系统的微分方程为 y (t) + 5y (t) + 6y(t) = 2x (t) + 8x(t) ,计算该系统 的单位冲激响应。 解:b=[2,8];a=[1,5,6]; t=0:0.1:10; y=impulse(b,a,t); (2) 用命令 step 求解系统的单位阶跃响应 step (sys):计算并画出系统的冲激响应,sys 可以是用命令 tf、zpk 或 ss 建立的系 统函数。 step (sys, t):计算并画出系统在向量 t 定义的时间内的冲激响应。 Y=step (sys, t):向量 Y 保存对应时间的系统输出值。 (3) 使用命令 lsim 求解系统在任意输入下的响应 lsim(sys, x, t)计算并画出任意输入下系统的零状态响应,sys 可以是用命令 tf、zpk 或 ss 建立的系统函数,t 为时间向量定义时间范围,x 为系统的输入。 lsim(sys, x, t, zi) 计算并画出系统的完全响应,但 sys 必须是状态空间形式的系统 函数,zi 为系统的初始状态。 Y=lsim(sys, x, t, zi):向量 Y 保存对应时间的系统输出值。 b=[2,8];a=[1,5,6]; sys=tf(b,a);