
第4章IIR数字滤波器的设计IIR滤波器设计的基本思想1)将数字滤波器的设计为模拟滤波器的设计。2)设计满足技术指标的模拟滤波器。3)将模拟滤波器转换为数字滤波器。4.1模拟低通滤波器的设计模拟滤波器的技术要求Butterworth模拟低通滤波器切比雪夫Ⅱ型模拟低通滤波器?切比雪夫Ⅱ型模拟低通滤波器椭圆低通滤波器模拟滤波器的技术要求(H(jo))0,:通带截止频率1-8.阻带截止频率0:+过渡带8p:通带波动8s:阻带阻带波动一通带-o-00",o,A,=-20log1e(1-)通带衰减(db)(passbandAttenuation)A,=-20log1o8阻带衰减(db)(stopbandAttenuation)滤波器的Gain函数G()-20log1/H(j) dB4.1.1 ButterworthLowpassfilter1H(jo)1+(0/0.)2NN:滤波器阶数
第 4 章 IIR 数字滤波器的设计 IIR 滤波器设计的基本思想 1)将数字滤波器的设计为模拟滤波器的设计。 2)设计满足技术指标的模拟滤波器。 3)将模拟滤波器转换为数字滤波器。 4.1 模拟低通滤波器的设计 • 模拟滤波器的技术要求 • Butterworth 模拟低通滤波器 • 切比雪夫 II 型模拟低通滤波器 • 切比雪夫 II 型模拟低通滤波器 • 椭圆低通滤波器 模拟滤波器的技术要求 p: 通带截止频率 s: 阻带截止频率 p: 通带波动 s: 阻带波动 20log (1 ) Ap = −20log10 (1− p ) 通带衰减(db)(passband Attenuation) Ap = − 10 − p As 10 s As = −20log10 s 阻带衰减(db )(stopband Attenuation) = −20log |H( j)| 1 0 通带 过渡带 阻带 p s s p 1− |H( j)| 1 0 通带 过渡带 阻带 p s s p 1− G()=20log10|H(j)| dB 滤波器的Gain函数 4.1.1 Butterworth Lowpass filter N c H j 2 2 1 ( / ) 1 ( ) + = N: 滤波器阶数
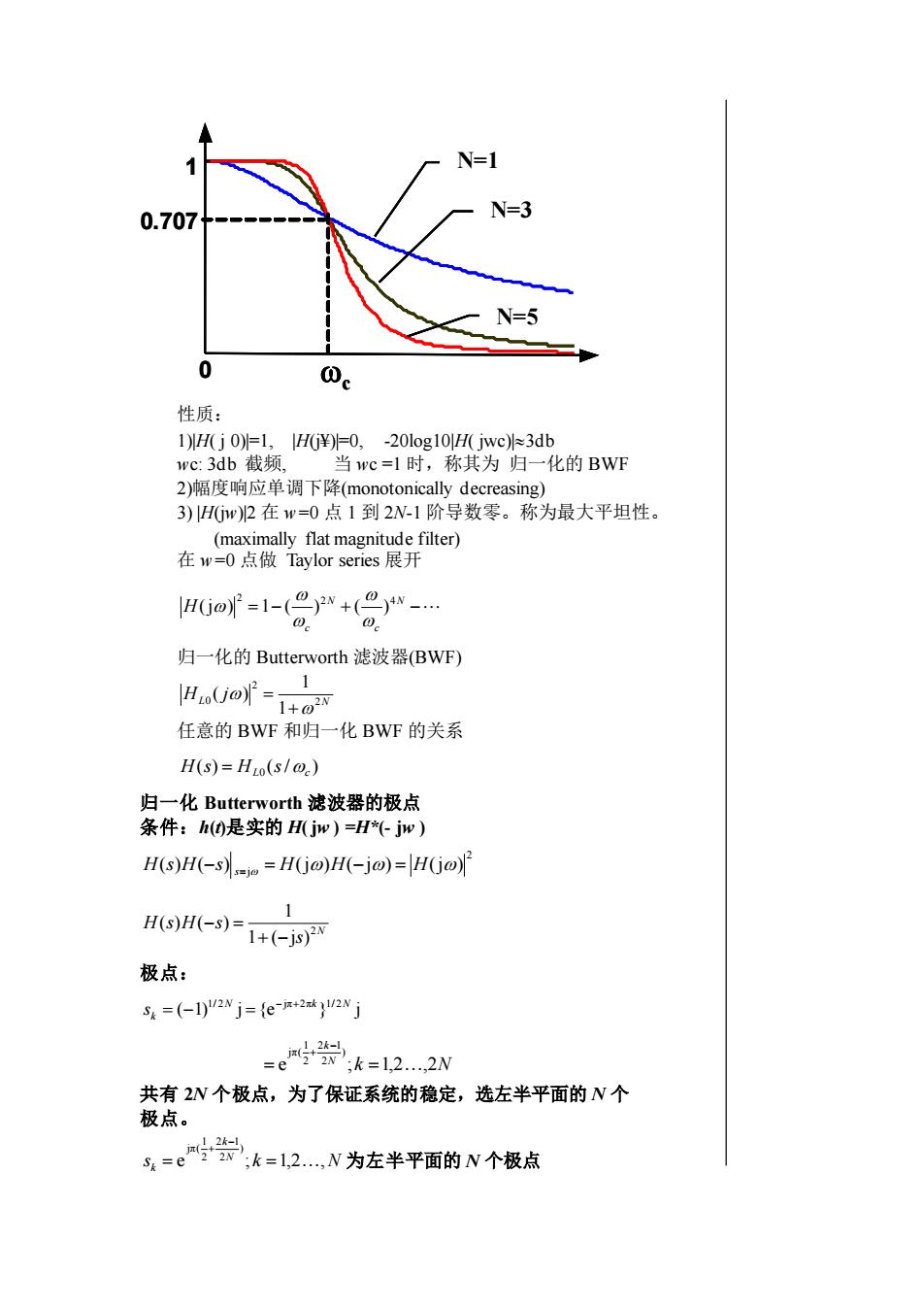
N=1N=30.707N=50Oc性质:1)H(j0)=1,[H()=0,-20log10|H(jwc)=3dbwc:3db截频当wc=1时,称其为归一化的BWF2)幅度响应单调下降(monotonicallydecreasing)3)|H(iw)2在w=0点1到2N-1阶导数零。称为最大平坦性。(maximally flat magnitude filter)在w=0点做Taylor series展开[H(jo) =1-(-)2N +(-)4N 00.归一化的Butterworth滤波器(BWF)1[Hro(jo)-1+02N任意的BWF和归一化BWF的关系H(s)=Ho(s / o.)归一化Butterworth滤波器的极点条件:h(t)是实的H(jw)=H*(-jw)H(s)H(-s) s=je = H(jo)H(-jo)=|H(jo)2H(s)H(-s)= 1+(js)2N极点:St =(-1)/2N j=[e-ji+2zk/1/2Njn(j+2k-22Nk=12....2N=e共有2N个极点,为了保证系统的稳定,选左半平面的N个极点。.1 2k-1inl22Nk=12....N为左半平面的N个极点S.=e
c 1 0 N=1 N=3 N=5 0.707 c 1 0 N=1 N=3 N=5 0.707 性质: 1)|H( j 0)|=1, |H(j¥)|=0, -20log10|H( jwc)|3db wc: 3db 截频, 当 wc =1 时,称其为 归一化的 BWF 2)幅度响应单调下降(monotonically decreasing) 3) |H(jw)|2 在 w=0 点 1 到 2N-1 阶导数零。称为最大平坦性。 (maximally flat magnitude filter) 在 w=0 点做 Taylor series 展开 = − + N − c N c H 2 4 2 (j ) 1 ( ) ( ) 归一化的 Butterworth 滤波器(BWF) L N H j 2 2 0 1 1 ( ) + = 任意的 BWF 和归一化 BWF 的关系 ( ) ( / ) L0 c H s = H s 归一化 Butterworth 滤波器的极点 条件:h(t)是实的 H( jw ) =H*(- jw ) 2 j ( ) ( ) (j) ( j) (j) H s H −s s= = H H − = H N s H s H s 2 1 ( j ) 1 ( ) ( ) + − − = 极点: ( 1) j {e } j 1/ 2N jπ 2πk 1/ 2N k s − + = − = N k N k e ; 1,2 ,2 ) 2 2 1 2 1 jπ( = = − + 共有 2N 个极点,为了保证系统的稳定,选左半平面的 N 个 极点。 s N k N k k e ; 1,2 , ) 2 2 1 2 1 jπ( = = − + 为左半平面的 N 个极点

-2k+1is(↓+2(N+I-k)-I1.2k-12)i---jn(-2N22N22NSN+I-k=e2=e=e=Sk(s-st)(s-$t)=s? -2Re(st)s+|sl2(2k-1))s +1= s2 +2sin(2N·当N为偶数时N/21H(s)=II$2 +2(sin @,)s+1klQ, =(2k-1)元/(2N)例: N=2,0=(2k-1)元/(2N)=p/4 ; k=11H(s)=s2+~2s+1例:N=4,0,=(2k-1)元/8=p/8,3p/8;k=1,21H(s)=(s2 +2 sin(元/8)s+1)(s2 +2 sin(3元/8)s+1)1(s? +0.7654s +1)(s +1.8478s+1)当 N为奇数时engia2N=eji =-1S(N+1)/2=e(N-1)/211H(s)5 +2(sin 0)s+1(s +1)k=l0=(2k-1)元/(2N)1例:N=1H(s)=(s+1)N=30 =(2 -1)元/(2×3) = 元/6IH(s)=(s+1(s? +$+1)
2) 2 2( 1 ) 1 2 1 jπ( 1 e − + − − + + − = N N k N k s ) 2 2 1 2 1 jπ( e N − k+ − + = ) 2 2 1 2 1 jπ( e N k− − + = k = s 2 2 ( )( ) 2Re( ) k k k k s − s s − s = s − s s + s ) 1 2 (2 1) 2sin( 2 + − = + s N k s • 当 N 为偶数时 2(sin ) 1 1 ( ) 2 / 2 1 + + == s s H s k N k (2k 1)π /(2N) k = − 例:N=2, (2k 1)π /(2N) k = − =p/4 ; k=1 2 1 1 ( ) 2 + + = s s H s 例:N=4, k = (2k −1)π /8=p / 8, 3 p / 8; k=1 ,2 ( 2sin( π /8) 1)( 2sin( 3π /8) 1) 1 ( ) 2 2 + + + + = s s s s H s ( 0.7654 1)( 1.8478 1) 1 2 2 + + + + = s s s s • 当 N 为奇数时 ) 2 2( 1)/ 2 1 2 1 jπ( ( 1)/ 2 e N N N s + − + + = e 1 jπ = = − 2(sin ) 1 1 ( 1) 1 ( ) 2 ( 1)/ 2 + 1 + + = − s = s s H s k N k (2k 1)π /(2N) k = − 例:N=1 ( 1) 1 ( ) + = s H s N=3 (2 1)π/(2 3) 1 = − = π/ 6 ( 1)( 1) 1 ( ) 2 + + + = s s s H s

例:设计一个满足下列指标BW型模拟滤波器p=0.1元,の=0.4元,A,=1dB,As=10dBlog1o|H(jo,)=-0.1AlogoH(jo,)=-0.1A,·H(jo)21+(0/0.)2N1+(2)2N =1004,1+()2N = 100.14,O0100.14, 1log1o()100.14,NZ=1.282log10(0, /0,)取N=2,将N=2带入通带满足的方程0p=0.44040(100.11)/41o?H(s)=s?+~20,$+0?()+~2()+110..0.44042$2+0.6228s+0.44042验证:Ap=0.9999db;As=18.2795db通带满足指标,阻带超过指标模拟Butterworth低通滤波器设计步骤:(1)由滤波器的设计指标wp、ws、Ap、As和式确定滤波器的(2)阶数N100.14,log1o0100.14,N≥2log1o(o, /o,)(2)确定wcOpQ(1014 -1)/2 ≤0. ≤(100.14, 1)/2N(3)确定滤波器的系统函数H(s)
例:设计一个满足下列指标 BW 型模拟滤波器 = 0.1 p , = 0.4 p = 0.1 , s = 0.4 , Ap = 1dB, As = 10dB p Ap log H( j ) 0.1 2 10 = − s As log H( j ) 0.1 2 10 = − N c H j 2 2 1 ( / ) 1 ( ) + = N Ap c p 2 0.1 1+ ( ) =10 N As c s 2 0.1 1+ ( ) =10 1.28 2log ( / ) ) 10 1 10 1 log ( 10 0.1 0.1 10 = − − p s A A s p N 取 N=2,将 N=2 带入通带满足的方程 0.4404 (10 1) 0.1 1/ 4 = − = p c 2 2 2 2 2 ( ) 2( ) 1 1 ( ) c c c c c s s s s H s + + = + + = 2 2 2 0.6228 0.4404 0.4404 + + = s s 验证: Ap=0.9999db ; As= 18.2795 db 通带满足指标,阻带超过指标 模拟 Butterworth 低通滤波器设计步骤: (1) 由滤波器的设计指标 wp、ws、Ap、As 和式确定滤波器的 (2) 阶数 N 2log ( / ) ) 10 1 10 1 log ( 10 0.1 0.1 10 p s A A s p N − − (2) 确定 wc A N 0.1A 1/ 2N s c 0.1 1/ 2 p (10 1) (10 1) p s − − (3)确定滤波器的系统函数 H(s)
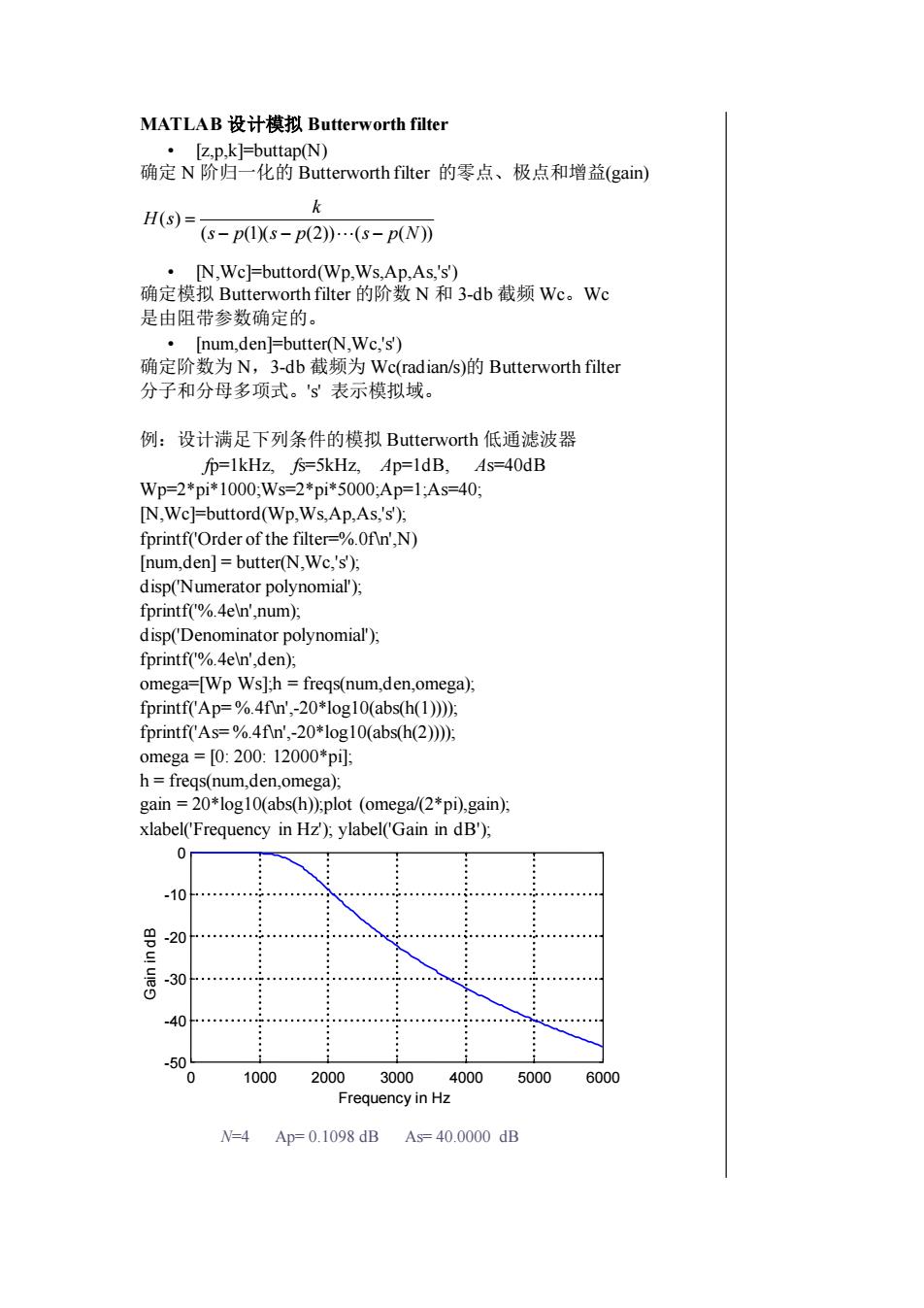
MATLAB设计模拟Butterworthfilter[z,p,k]-buttap(N)·确定N阶归一化的Butterworthfilter的零点、极点和增益(gain)kH(s) =(s- p(1)(s- p(2)..-(s- p(N)N,Wc-buttord(Wp,Ws,Ap,As,'s)确定模拟Butterworthfilter的阶数N和3-db截频Wc。Wc是由阻带参数确定的。[num,den]-butter(N,Wc,'s')确定阶数为N,3-db截频为Wc(radian/s)的Butterworthfilter分子和分母多项式。"s表示模拟域。例:设计满足下列条件的模拟Butterworth低通滤波器fp=1kHz,fs=5kHz,Ap=1dB,As=40dBWp=2*pi*1000;Ws=2*pi*5000Ap=1;As=40[N,Wc]-buttord(Wp, Ws,Ap,As,'s);fprintf(Orderofthefilter=%.Ofln',N)[num,den] = butter(N,We,'s');disp(Numeratorpolynomial');fprintf(%.4eln',num),disp(Denominator polynomial);fprintf(%.4eln',den);omega-[Wp Ws];h = freqs(num,den,omega),fprintf(Ap=%.4f/n',-20*log10(abs(h(1);fprintf(As=%.4fin',-20*log10(abs(h(2);0mega =[0:200:12000*pi];h=freqs(num,den,omega);gain = 20*log10(abs(h);plot (omega/(2*pi),gain);xlabel(Frequency in Hz); ylabel(Gain in dB');0-10apuui-20-30O..-40.........*-501000200030004000500060000FrequencyinHzN=4Ap=0.1098dBAs=40.0000dB
MATLAB 设计模拟 Butterworth filter • [z,p,k]=buttap(N) 确定 N 阶归一化的 Butterworth filter 的零点、极点和增益(gain) ( (1)( (2)) ( ( )) ( ) s p s p s p N k H s − − − = • [N,Wc]=buttord(Wp,Ws,Ap,As,'s') 确定模拟 Butterworth filter 的阶数 N 和 3-db 截频 Wc。Wc 是由阻带参数确定的。 • [num,den]=butter(N,Wc,'s') 确定阶数为 N,3-db 截频为 Wc(radian/s)的 Butterworth filter 分子和分母多项式。's' 表示模拟域。 例:设计满足下列条件的模拟 Butterworth 低通滤波器 fp=1kHz, fs=5kHz, Ap=1dB, As=40dB Wp=2*pi*1000;Ws=2*pi*5000;Ap=1;As=40; [N,Wc]=buttord(Wp,Ws,Ap,As,'s'); fprintf('Order of the filter=%.0f\n',N) [num,den] = butter(N,Wc,'s'); disp('Numerator polynomial'); fprintf('%.4e\n',num); disp('Denominator polynomial'); fprintf('%.4e\n',den); omega=[Wp Ws];h = freqs(num,den,omega); fprintf('Ap= %.4f\n',-20*log10(abs(h(1)))); fprintf('As= %.4f\n',-20*log10(abs(h(2)))); omega = [0: 200: 12000*pi]; h = freqs(num,den,omega); gain = 20*log10(abs(h));plot (omega/(2*pi),gain); xlabel('Frequency in Hz'); ylabel('Gain in dB'); 0 1000 2000 3000 4000 5000 6000 -50 -40 -30 -20 -10 0 Frequency in Hz Gain ni dB N=4 Ap= 0.1098 dB As= 40.0000 dB