
第5章随机信号功率谱估计5.1平稳随机信号的数字特征平稳随机信号是指对时间的变化具有某种平稳性质的一类信号,可分为严格平稳和宽平稳信号两种。在实际中,往往把所要研究的随机信号视为宽平稳的。稳信号在时域上可以利用其数字特征来进行描述:设离散随机信号x[k],Y[k]均值:mx[k]=E(X[k]),其MATLAB实现为M=mean(X);方差:α,=E((X[k]-m[K])"),其MATLAB实现为s=std(X);自相关函数:Rx[k1,k2]=E(X[ki]X[k2]),其MATLAB实现为c=xcorr(x);互相关函数:Rxy[k,k2]-E(X[ki]Y[k2]),其MATLAB实现为c=xcorr(x,y)。例:产生两个正弦信号加白噪声的样本数据,并绘出其互相关函数图。解:N=256;f=.1;M-N/4;x=5*sin(2*pi*f*(0:N-1)+2*randn(1,N);y=3*sin(2*pi*f*(0:N-1)+ randn(1,N);subplot(2,2,1)plot(x(1:N/2);xlabel(随机信号x);gridonsubplot(22,2);plot(y(1:N/2));xlabel(随机信号y);gridon;corrxy=xcorr(x,y,M);subplot(22,3);plot(-M:M),corrxy);xlabel(互相关函数);gridon;UMWWWWWDC随机信号0随机信号
第 5 章 随机信号功率谱估计 5.1 平稳随机信号的数字特征 平稳随机信号是指对时间的变化具有某种平稳性质的一类信号,可分为严格 平稳和宽平稳信号两种。在实际中,往往把所要研究的随机信号视为宽平稳的。平 稳信号在时域上可以利用其数字特征来进行描述: 设离散随机信号 X[k],Y[k] 均值:mx[k] = E{X[k]} ,其 MATLAB 实现为 M=mean(X); 方差: 2 2 x = E{(X[k]-m [k] ) } x ,其 MATLAB 实现为 s=std(X); 自相关函数:Rx[k1,k2]=E{ X[k1]X[k2] },其 MATLAB 实现为 c=xcorr (x); 互相关函数:Rxy[k1,k2]=E{ X[k1]Y[k2] },其 MATLAB 实现为 c=xcorr (x,y)。 例:产生两个正弦信号加白噪声的样本数据,并绘出其互相关函数图。 解:N=256;f=.1;M=N/4; x=5*sin(2*pi*f*(0:N-1))+2*randn(1,N); y=3*sin(2*pi*f*(0:N-1))+ randn(1,N); subplot(2,2,1);plot(x(1:N/2));xlabel('随机信号 x');grid on; subplot(2,2,2);plot(y(1:N/2)); xlabel('随机信号 y');grid on; corrxy=xcorr(x,y,M); subplot(2,2,3);plot((-M:M),corrxy); xlabel('互相关函数');grid on;

5.2功率谱估计功率谱估计是随机信号处理中的一个重要的研究和应用领域。功率谱估计基本上可以分为经典法和现代法。5.2.1经典谱估计经典谱估计是基于FFT算法的非参数估计,对足够长的记录数据效果较好。主要有自相关法和周期图法。相关法法就是根据维纳一辛钦定理,先由随机信号的样本x[k]估计出其自相关函数R,[n],然后对R,[n]进行DTFT就可以得到随机信号的功率谱估计。周期图法是将随机信号的N点观察值xN[k]看成能量有限的信号,取其傅立叶变换,得X~(e),然后取其幅值的平方,并除以N作为随机信号的功率谱估计。即:I (2)=Xx(e)NI在工程实际中,经典功率谱估计法获得广泛应用的是改进后的平均周期图法。该方法采取数据分段加窗处理再求平均的办法。通过求各段功率谱平均,最后得到功率谱估计。在MATLAB信号处理工具箱中,提供了随机信号经典功率谱估计的各种函数。(1)函数periodogram可以实现周期图法的功率谱估计,其调用格式为[Pxx,F]=PERIODOGRAM(x, WINDOW,NFFT,Fs)其中,x为进行功率谱估计的输入有限长序列:WINDOW用于指定采用的窗函数默认值为矩形窗(boxcar),窗函数的长度等于输入序列x的长度;NFFT为DFT的点数,一般取大于输入序列x的长度,默认值为256;Fs是绘制功率谱曲线的抽样频率,默认值为1;Pxx为功率谱估计值;F为Pxx值所对应的频率点。(2)Welch-Bartlett平均周期图法可以利用函数psd实现,其调用格式为[Pxx,F]= PSD(x, NFFT, Fs, WINDOW, NOVERLAP)其中,参数x,NFFT,Fs用法同periodogram函数;WINDOW用于指定采用的窗函数,默认值为hanning窗NOVERLAP指定分段重叠的样本数。如果使用boxcar窗,且NOVERLAP=O,则可得到Bartlett法的平均周期图。如果NOVERLAP=length(x)/2,则可得到重叠50%的Welch法平均周期图
5.2 功率谱估计 功率谱估计是随机信号处理中的一个重要的研究和应用领域。功率谱估计基本 上可以分为经典法和现代法。 5.2.1 经典谱估计 经典谱估计是基于 FFT 算法的非参数估计,对足够长的记录数据效果较好。主 要有自相关法和周期图法。相关法法就是根据维纳-辛钦定理,先由随机信号的样 本 x[k]估计出其自相关函数 ˆ [ ] R n x ,然后对 ˆ [ ] R n x 进行 DTFT 就可以得到随机信号 的功率谱估计。周期图法是将随机信号的 N 点观察值 xN[k]看成能量有限的信号, 取其傅立叶变换,得 ( ) j X e N ,然后取 其幅值的平方,并除以 N 作为随机信号的 功率谱估计。即: ( ) N I = 1 2 ( ) j X e N N 在工程实际中,经典功率谱估计法获得广泛应用的是改进后的平均周期图法。该方 法采取数据分段加窗处理再求平均的办法。通过求各段功率谱平均,最后得到功率 谱估计。 在 MATLAB 信号处理工具箱中,提供了随机信号经典功率谱估计的各种函数。 (1) 函数 periodogram 可以实现周期图法的功率谱估计,其调用格式为 [Pxx,F] = PERIODOGRAM(x, WINDOW,NFFT,Fs) 其中,x 为进行功率谱估计的输入有限长序列;WINDOW 用于指定采用的窗函数, 默认值为矩形窗(boxcar),窗函数的长度等于输入序列 x 的长度;NFFT 为 DFT 的 点数,一般取大于输入序列 x 的长度,默认值为 256;Fs 是绘制功率谱曲线的抽样 频率,默认值为 1;Pxx 为功率谱估计值;F 为 Pxx 值所对应的频率点。 (2) Welch-Bartlett 平均周期图法可以利用函数 psd 实现,其调用格式为 [Pxx,F] = PSD(x, NFFT, Fs, WINDOW, NOVERLAP) 其中,参数 x,NFFT,Fs 用法同 periodogram 函数;WINDOW 用于指定采用的窗函 数,默认值为 hanning 窗;NOVERLAP 指定分段重叠的样本数。如果使用 boxcar 窗,且 NOVERLAP=0,则可得到 Bartlett 法的平均周期图。如果 NOVERLAP=length(x)/2,则可得到重叠 50%的 Welch 法平均周期图
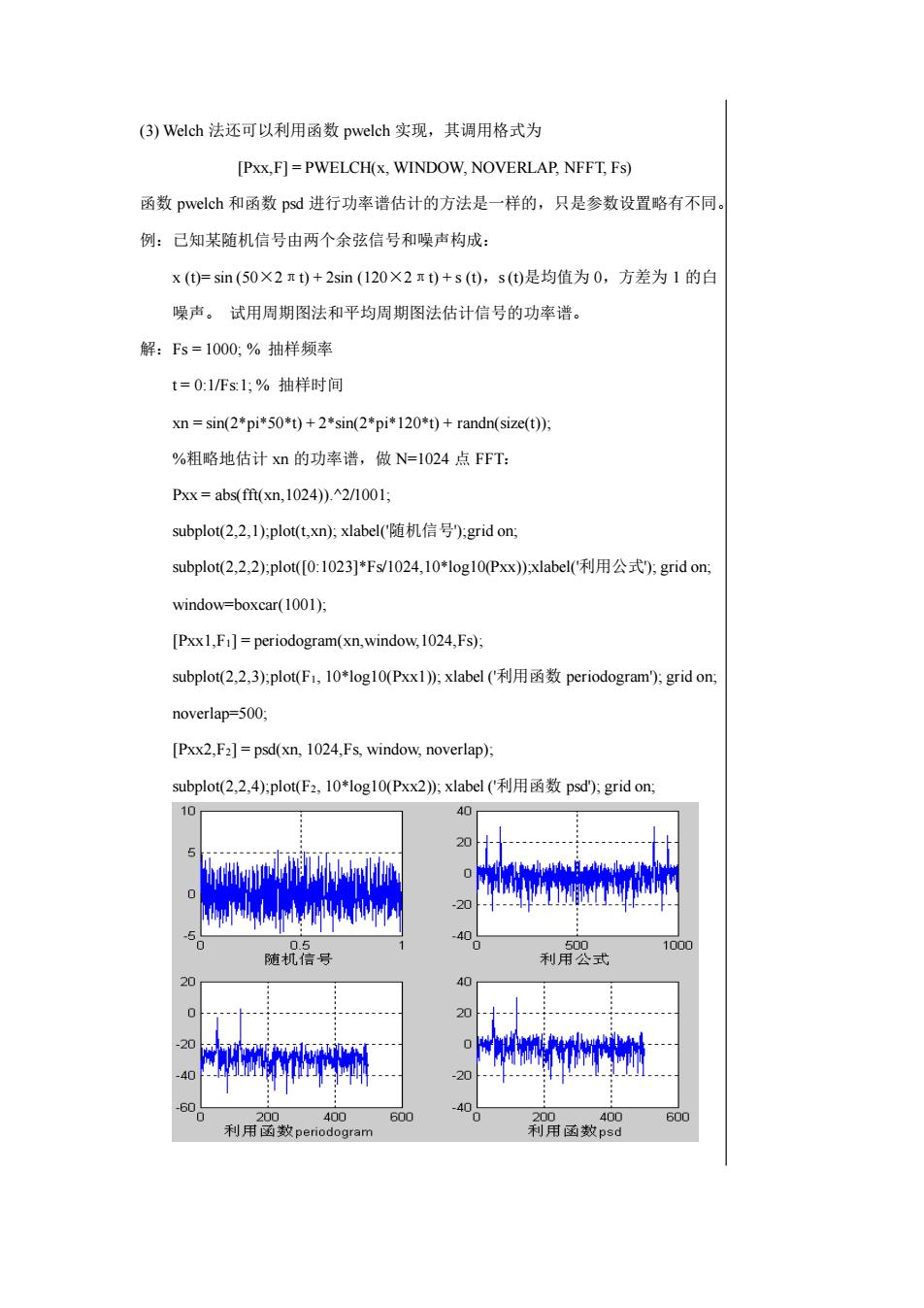
(3)Welch法还可以利用函数pwelch实现,其调用格式为[Pxx,F]=PWELCH(x,WINDOW,NOVERLAP, NFFT, Fs)函数pwelch和函数psd进行功率谱估计的方法是一样的,只是参数设置略有不同。例:已知某随机信号由两个余弦信号和噪声构成:x(t)=sin(50×2πt)+2sin(120×2元t)+s(t),s(t)是均值为0,方差为1的白噪声。试用周期图法和平均周期图法估计信号的功率谱。解:Fs=1000:%抽样频率t=0:1/Fs:1:%抽样时间xn = sin(2*pi*50*t)+2*sin(2*pi*120*t)+ randn(size(t);%粗略地估计xn的功率谱,做N=1024点FFT:Pxx=abs(ft(xn,1024)).^2/1001;subplot(2,2,1);plot(t,xn);xlabel(随机信号);gridon;subplot(2,2,2);plot([0:1023]*Fs/1024,10*log10(Pxx);xlabel(利用公式);gridon;window=boxcar(1001);[Pxx1,Fi]= periodogram(xn,window,1024,Fs);subplot(2,2,3);plot(F1,10*log10(Pxx1);xlabel(利用函数periodogram);gridonnoverlap=500,[Pxx2,F2]=psd(xn, 1024,Fs, window,noverlap);subplot(2,2,4);plot(F2,10*log10(Pxx2);xlabel(利用函数psd);gridon;价H400.55001000随机信号利用公式20402040200600400200400600利用函数psd利用函数periodogram
(3) Welch 法还可以利用函数 pwelch 实现,其调用格式为 [Pxx,F] = PWELCH(x, WINDOW, NOVERLAP, NFFT, Fs) 函数 pwelch 和函数 psd 进行功率谱估计的方法是一样的,只是参数设置略有不同。 例:已知某随机信号由两个余弦信号和噪声构成: x (t)= sin (50×2πt) + 2sin (120×2πt) + s (t),s (t)是均值为 0,方差为 1 的白 噪声。 试用周期图法和平均周期图法估计信号的功率谱。 解:Fs = 1000; % 抽样频率 t = 0:1/Fs:1; % 抽样时间 xn = sin(2*pi*50*t) + 2*sin(2*pi*120*t) + randn(size(t)); %粗略地估计 xn 的功率谱,做 N=1024 点 FFT: Pxx = abs(fft(xn,1024)).^2/1001; subplot(2,2,1);plot(t,xn); xlabel('随机信号');grid on; subplot(2,2,2);plot([0:1023]*Fs/1024,10*log10(Pxx));xlabel('利用公式'); grid on; window=boxcar(1001); [Pxx1,F1] = periodogram(xn,window,1024,Fs); subplot(2,2,3);plot(F1, 10*log10(Pxx1)); xlabel ('利用函数 periodogram'); grid on; noverlap=500; [Pxx2,F2] = psd(xn, 1024,Fs, window, noverlap); subplot(2,2,4);plot(F2, 10*log10(Pxx2)); xlabel ('利用函数 psd'); grid on;

5.2.2现代谱估计利用经典法进行功率谱估计,频率分辨率较低,其原因是对周期图法假定数据窗以外的数据全为零,而自相关法是假定在延迟窗以外的自相关函数全为零。当然这种假定是不符合实际的。正是由于这些不符合实际的假设产生了经典谱估计较差的频率分辨率。基于参数建模的功率谱估计是现代谱估计的重要内容,其目的就是为了改善功率谱估计的频率分辨率,它主要包括AR模型,MA模型,ARMA模型等。基于参数建模的功率谱估计方法的基本思路是:1)建立一个由白噪声序列S[k]就可以产生平稳信号序列x[k]的系统H(z);2由已知的序列x[k]或其自相关函数Rx[n]估计出系统H(z)的参数;3)根据 H(z)的参数估计序列x[k)的功率谱P,(Q)。MATLAB信号处理工具箱中定义了一些函数实现现代谱估计:(1)函数levinson可以实现L-D递推算法求解AR模型参数及白噪声序列的方差,其调用格式为:A=LEVINSON(R,ORDER)其中,ORDER为AR模型的阶数;R为观测序列的自相关函数;返回值A即为白噪声序列的方差和AR模型参数。(2)函数aryule也可以实现L-D递推算法,其调用格式为:[A,E,K]=ARYULE(X, ORDER)其中,ORDER为AR模型的阶数;X为观测序列:返回值A即为白噪声序列的方差和AR模型参数;E为预测误差;K为反射系数。(3)Burge算法可以利用arburg实现,其调用格式为:[A,E,K]=ARBURG (X, ORDER)式中参数与函数aryule相同。(4)利用函数pyulear可以实现基于L-D递推算法的AR模型功率谱估计,其调用格式为:Pxx=PYULEAR(X,ORDER)其中,X为观测序列:ORDER为AR模型的阶数。(5)基于Burg算法的AR模型功率谱估计可以利用函数pburg实现,其调用格
5.2.2 现代谱估计 利用经典法进行功率谱估计,频率分辨率较低,其原因是对周期图法假定数据 窗以外的数据全为零,而自相关法是假定在延迟窗以外的自相关函数全为零。当然 这种假定是不符合实际的。正是由于这些不符合实际的假设产生了经典谱估计较差 的频率分辨率。 基于参数建模的功率谱估计是现代谱估计的重要内容,其目的就是为了改善功 率谱估计的频率分辨率,它主要包括 AR 模型,MA 模型,ARMA 模型等。基于参 数建模的功率谱估计方法的基本思路是: 1) 建立一个由白噪声序列 S[k]就可以产生平稳信号序列 x[k]的系统 H(z); 2) 由已知的序列 x[k]或其自相关函数 Rx[n]估计出系统 H(z)的参数; 3) 根据 H(z)的参数估计序列 x[k]的功率谱 ˆ ( ) P x 。 MATLAB 信号处理工具箱中定义了一些函数实现现代谱估计: (1) 函数 levinson 可以实现 L-D 递推算法求解 AR 模型参数及白噪声序列的方 差,其调用格式为 : A = LEVINSON(R, ORDER) 其中,ORDER 为 AR 模型的阶数;R 为观测序列的自相关函数;返回值 A 即 为白噪声序列的方差和 AR 模型参数。 (2) 函数 aryule 也可以实现 L-D 递推算法,其调用格式为 : [A,E,K] = ARYULE(X, ORDER) 其中,ORDER 为 AR 模型的阶数;X 为观测序列;返回值 A 即为白噪声序列 的方差和 AR 模型参数;E 为预测误差;K 为反射系数。 (3) Burge 算法可以利用 arburg 实现,其调用格式为 : [A,E,K] =ARBURG (X, ORDER) 式中参数与函数 aryule 相同。 (4) 利用函数 pyulear 可以实现基于 L-D 递推算法的 AR 模型功率谱估计,其 调用格式为 : Pxx= PYULEAR(X, ORDER) 其中,X 为观测序列;ORDER 为 AR 模型的阶数。 (5)基于 Burg 算法的 AR 模型功率谱估计可以利用函数 pburg 实现,其调用格
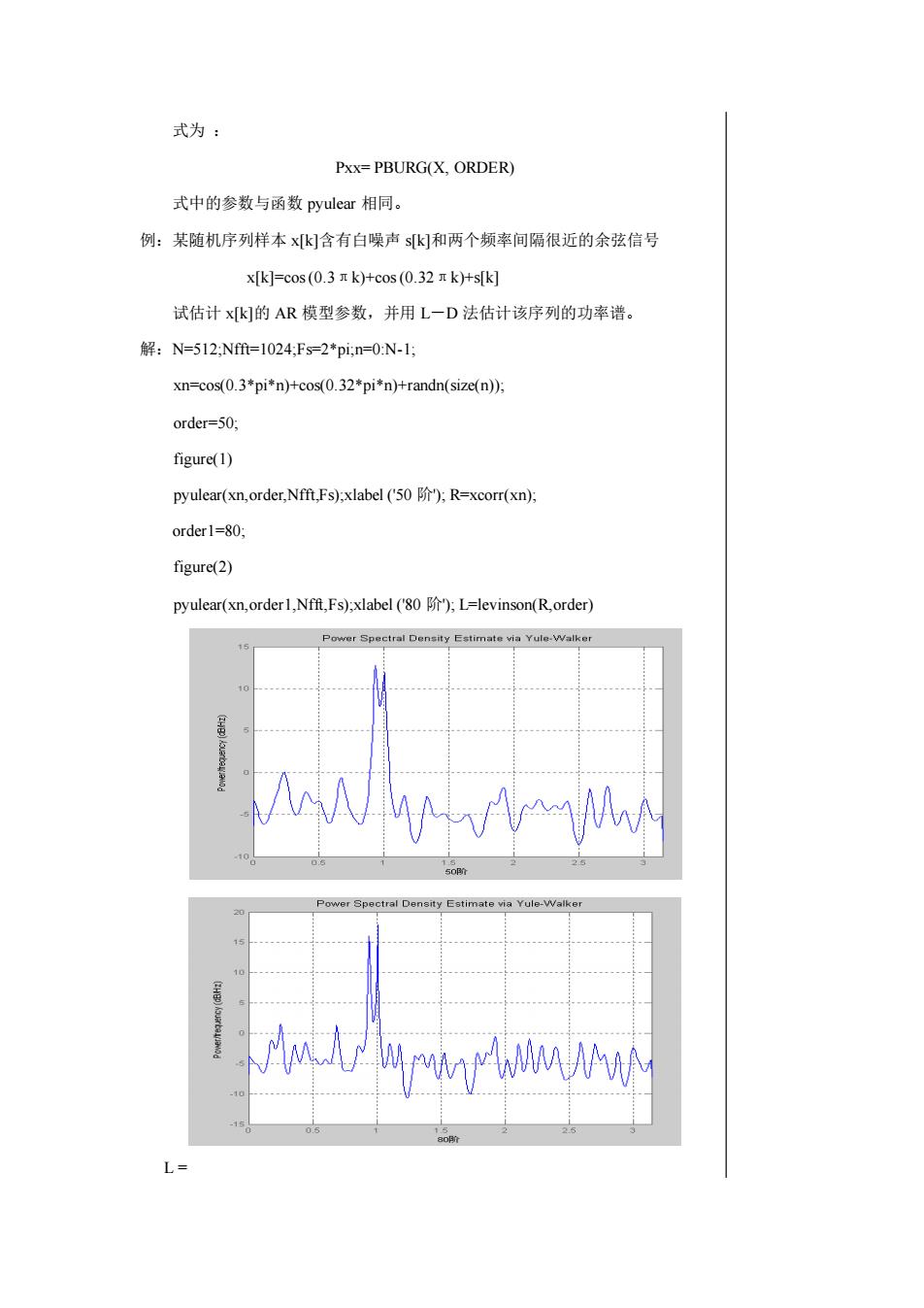
式为:PxX=PBURG(X,ORDER)式中的参数与函数pyulear相同。例:某随机序列样本x[k]含有白噪声s[k]和两个频率间隔很近的余弦信号x[k]=cos (0.3 πk)+cos (0.32 πk)+s[k]试估计x[k]的AR模型参数,并用L一D法估计该序列的功率谱。解: N=512;Nfft=1024;Fs-2*pi;n=0:N-1,xn=cos(0.3*pi*n)+cos(0.32*pi*n)+randn(size(n));order=50;figure(1)pyulear(xn,order,Nfft,Fs);xlabel ('50 阶"); R=xcorr(xn);order1=80;figure(2)pyulear(xn,order1,Nff,Fs);xlabel (80 阶"); L=levinson(R,order)PowerSpectral Density Estimate via Yule-WalkeZHBww0AcraeHHmAMwL=
式为 : Pxx= PBURG(X, ORDER) 式中的参数与函数 pyulear 相同。 例:某随机序列样本 x[k]含有白噪声 s[k]和两个频率间隔很近的余弦信号 x[k]=cos (0.3πk)+cos (0.32πk)+s[k] 试估计 x[k]的 AR 模型参数,并用 L-D 法估计该序列的功率谱。 解:N=512;Nfft=1024;Fs=2*pi;n=0:N-1; xn=cos(0.3*pi*n)+cos(0.32*pi*n)+randn(size(n)); order=50; figure(1) pyulear(xn,order,Nfft,Fs);xlabel ('50 阶'); R=xcorr(xn); order1=80; figure(2) pyulear(xn,order1,Nfft,Fs);xlabel ('80 阶'); L=levinson(R,order) L =