
7.6习题7-1.已知某数字系统的系统函数为23H(-)=(z-0.4)(-2-0.6z+0.25)试分别画出直接型、级联型、并联型结构框图。解:将H(-)表示为1H(=)=1 =~l + 0.49≥2 0.1=-3由此可画出系统的直接型结构框图,如下图(a)所示。由于系统有一单实数极点和一对共轭复数极点,故将H=)表示实系数一阶、二阶子系统的乘积,即11H(=)=1 0.4" 1 0.62l + 0.252~2由此可画出系统的级联型结构框图,如下图(b)所示。故将H(=)表示实系数一阶、二阶子系统之和0.0588 +0.5882z-10.9412H(=)=10.62-" +0.25--210.4z-l由此可画出系统的并联型结构框图,如下图(c)所示。x[K]-1x[k]y[k]0.490.60.0.10.25(a)直接型结构(b)级联型结构
7.6 习题 7-1. 已知某数字系统的系统函数为 ( 0.4)( 0.6 0.25) ( ) 2 3 − − + = z z z z H z 试分别画出直接型、级联型、并联型结构框图。 解: 将 H(z)表示为 1 2 3 1 0.49 0.1 1 ( ) − − − − + − = z z z H z 由此可画出系统的直接型结构框图,如下图(a)所示。由于系统有一单实数极点和一对共轭 复数极点,故将 H(z)表示实系数一阶、二阶子系统的乘积,即 1 1 2 1 0.6 0.25 1 1 0.4 1 ( ) − − − − − + = z z z H z 由此可画出系统的级联型结构框图,如下图(b)所示。故将 H(z)表示实系数一阶、二阶子系 统之和 1 2 1 1 1 0.6 0.25 0.0588 0.5882 1 0.4 0.9412 ( ) − − − − − + + + − = z z z z H z 由此可画出系统的并联型结构框图,如下图(c)所示。 x[k] y[k] 0.1 z −1 z −1 z −1 −0.49 x[k] y[k] z −1 z −1 −0.25 0.6 z −1 0.4 (a) 直接型结构 (b) 级联型结构
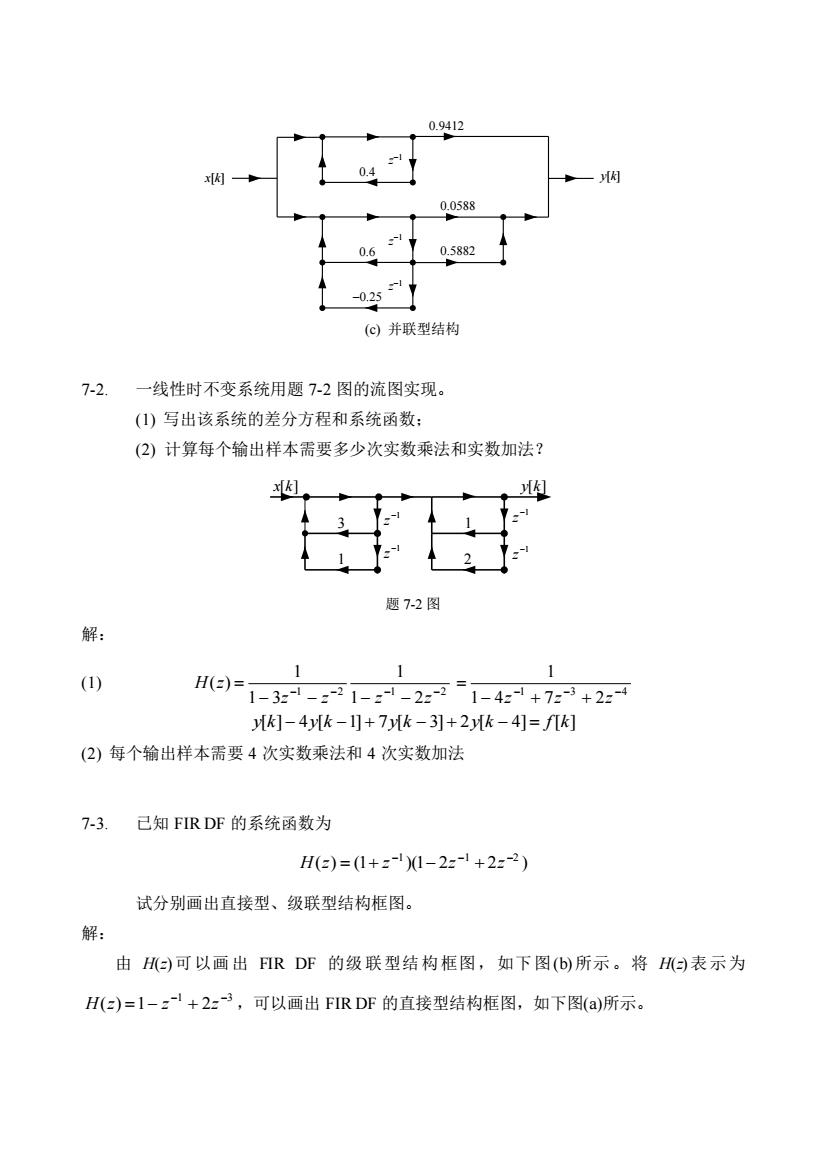
0.94121x[]0.05880.58820.60.25(c)并联型结构7-2.一线性时不变系统用题7-2图的流图实现。(1)写出该系统的差分方程和系统函数;(2)计算每个输出样本需要多少次实数乘法和实数加法?K]JA]题7-2图解:111(1)H(=):1 3-- - 2-2 1- --1 - 2--21 4=-l + 7=-3 + 2=-4[k]-4y[k-]]+7y[k-3]+2[k-4]= f[k](2)每个输出样本需要4次实数乘法和4次实数加法7-3.已知FIRDF的系统函数为H(=) = (1+ =-l )(1 2=-l + 22-2 )试分别画出直接型、级联型结构框图。解:由H()可以画出FIRDF的级联型结构框图,如下图(b)所示。将H(a)表示为H(=)=1-2-+2=-3,可以画出FIRDF的直接型结构框图,如下图(a)所示
x[k] y[k] z −1 z −1 −0.25 0.6 z −1 0.4 0.9412 0.0588 0.5882 (c) 并联型结构 7-2. 一线性时不变系统用题 7-2 图的流图实现。 (1) 写出该系统的差分方程和系统函数; (2) 计算每个输出样本需要多少次实数乘法和实数加法? 2 3 1 −1 z x[k] y[k] −1 z −1 z −1 z 1 题 7-2 图 解: (1) 1 2 1 2 1 2 1 1 3 1 ( ) − − − − − − − − = z z z z H z 1 3 4 1 4 7 2 1 − − − − + + = z z z y[k] − 4y[k −1] + 7y[k − 3] + 2y[k − 4] = f[k] (2) 每个输出样本需要 4 次实数乘法和 4 次实数加法 7-3. 已知 FIR DF 的系统函数为 ( ) (1 )(1 2 2 ) −1 −1 −2 H z = + z − z + z 试分别画出直接型、级联型结构框图。 解: 由 H(z) 可以画出 FIR DF 的级联型结构框图,如下图(b) 所示。将 H(z) 表示为 1 3 ( ) 1 2 − − H z = − z + z ,可以画出 FIR DF 的直接型结构框图,如下图(a)所示
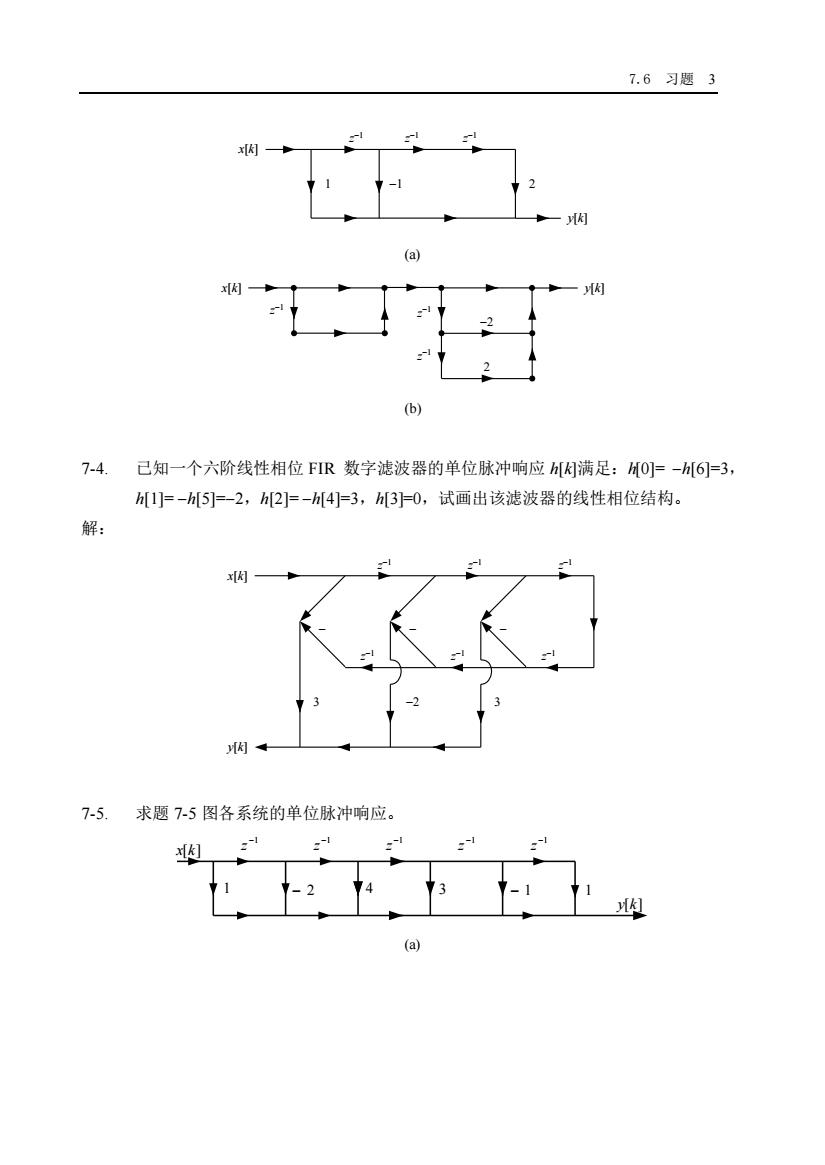
7.6习题32x[K](a)[]x[K]-2(b)7-4.已知一个六阶线性相位FIR数字滤波器的单位脉冲响应h[k]满足:h[0]=-h[6]=3h[1]=-h[5]=-2,h[2]=-h[4]=3,h[3]=0,试画出该滤波器的线性相位结构。解:x[]7-5.求题7-5图各系统的单位脉冲响应。~x[]K(a)
7.6 习题 3 −1 z −1 z −1 z −1 1 2 y[k] x[k] (a) x[k] y[k] z −1 −2 z −1 z −1 2 (b) 7-4. 已知一个六阶线性相位 FIR 数字滤波器的单位脉冲响应 h[k]满足:h[0]= −h[6]=3, h[1]= −h[5]=−2,h[2]= −h[4]=3,h[3]=0,试画出该滤波器的线性相位结构。 解: y[k] x[k] − z −1 z −1 z −1 z −1 z −1 −2 − − z −1 7-5. 求题 7-5 图各系统的单位脉冲响应。 −1 z −1 z −1 z − 2 3 y[k] x[k] 1 4 −1 z −1 z − 1 1 (a)
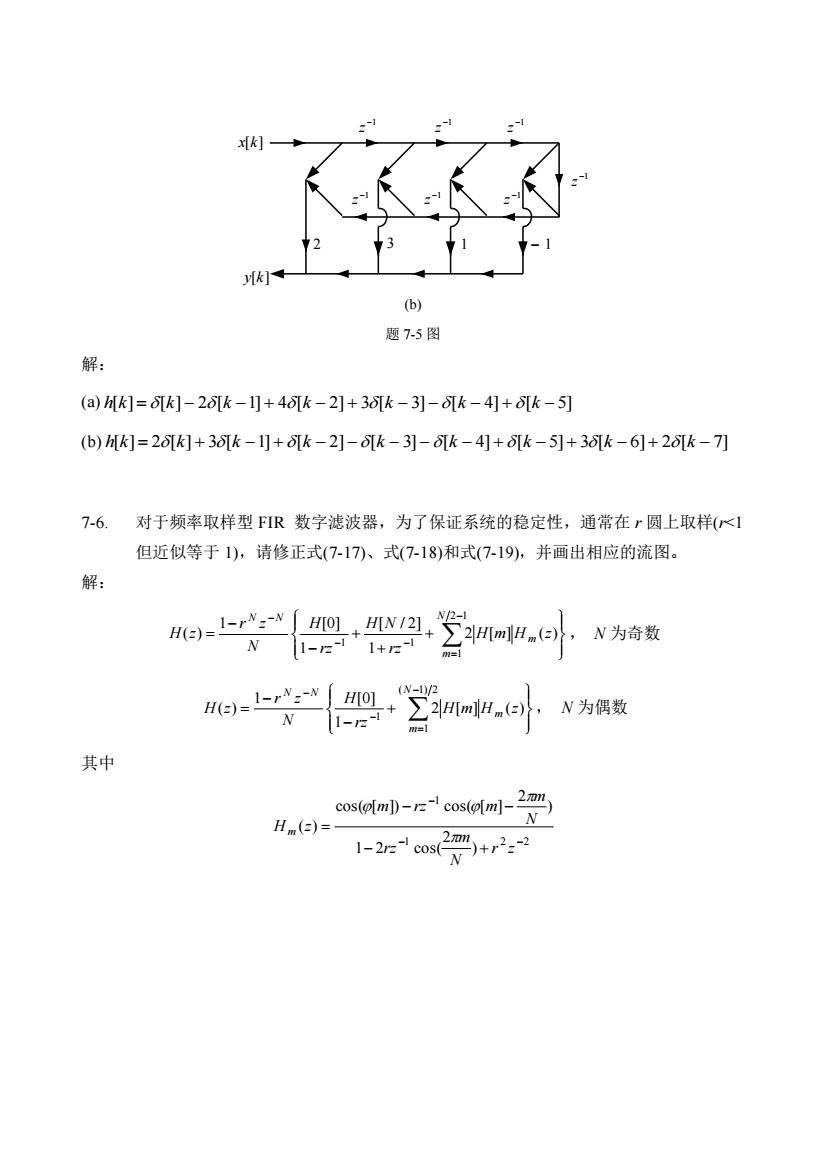
x[k][k](b)题7-5图解:(a)[k]=[k]-2[k-1]+ 4[k-2]+ 3[k -3]-[k- 4]+[k-5](b) h[k]=2[k]+ 3[k-1]+o[k-2]-o[k-3]-[k- 4]+[k-5]+3[k-6]+20[k -7]7-6.对于频率取样型FIR数字滤波器,为了保证系统的稳定性,通常在r圆上取样(<1但近似等于1),请修正式(7-17)、式(7-18)和式(7-19),并画出相应的流图解:N/2-11-rNNH[0]H[N /2]H(2)=22HmHm(-)N为奇数N1+72-1[1-2-]m=l(N-1)/21-rN2-NH[0]N为偶数H(=)=>2|H[m]Hm(=)N-1-rzm=l其中2mcos(o[m))-r=-lcos(o[m)-NHm(α)=2元m2-~212rz-lcos+N
−1 z −1 z −1 z −1 z −1 z −1 z −1 z x[k] y[k] 2 3 1 − 1 (b) 题 7-5 图 解: (a) h[k] =[k] − 2[k −1] + 4[k − 2] + 3[k − 3] −[k − 4] + [k − 5] (b) h[k] = 2[k] + 3[k −1] + [k − 2] −[k − 3] −[k − 4] + [k − 5] + 3[k − 6] + 2[k − 7] 7-6. 对于频率取样型 FIR 数字滤波器,为了保证系统的稳定性,通常在 r 圆上取样(r<1 但近似等于 1),请修正式(7-17)、式(7-18)和式(7-19),并画出相应的流图。 解: + + + − − = − = − − − 2 1 1 1 1 2 [ ] ( ) 1 [ / 2] 1 1 [0] ( ) N m m N N H m H z rz H N rz H N r z H z , N 为奇数 + − − = − = − − ( 1) 2 1 1 2 [ ] ( ) 1 1 [0] ( ) N m m N N H m H z rz H N r z H z , N 为偶数 其中 1 2 2 1 ) 2 1 2 cos( ) 2 cos( [ ]) cos( [ ] ( ) − − − − + − − = r z N m rz N m m rz m Hm z
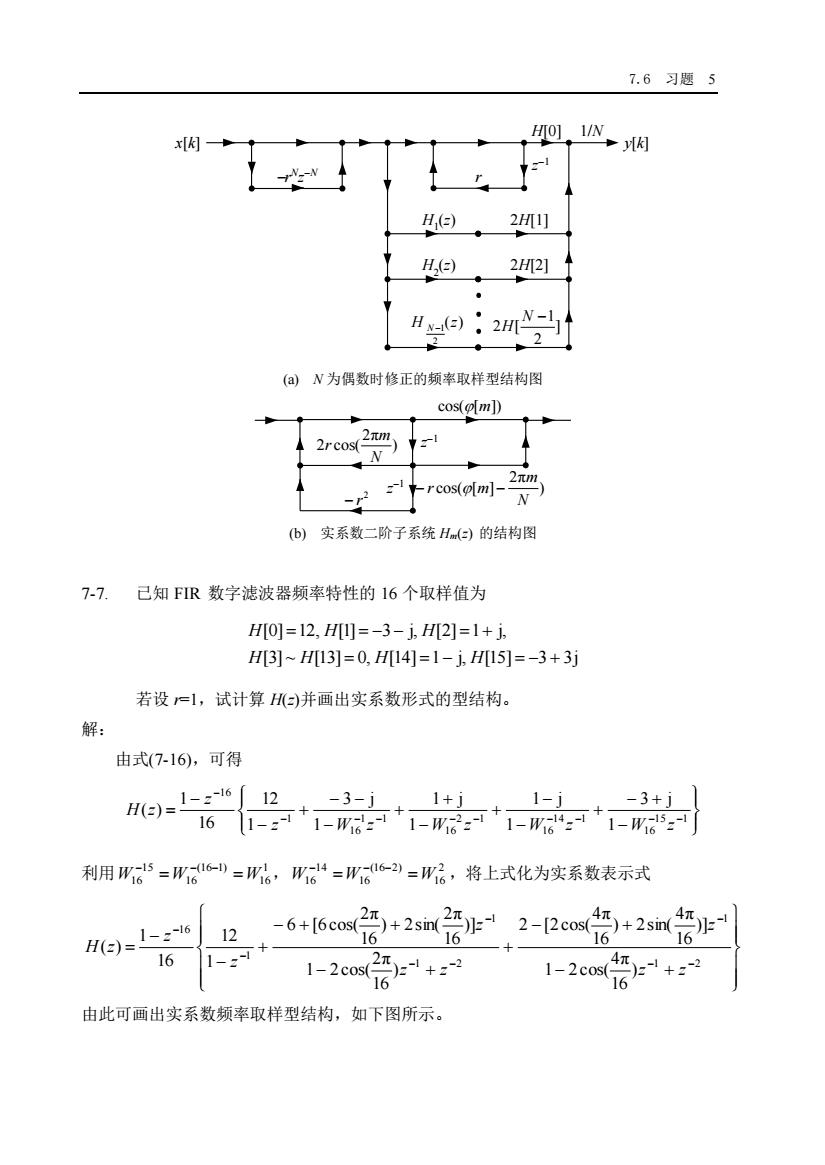
7.6习题5H[O]1/Ny[k]x[k]H()2H[1]H,(2)2H[2]H n-(2) :2H(a)N为偶数时修正的频率取样型结构图cos([m)2元m-I2rcos(2元mrcos(o[m]L(b)实系数二阶子系统Hm(=)的结构图7-7.已知FIR数字滤波器频率特性的16个取样值为H[0]=12,H[I]=-3-i, H[2]=1+ jH[3] ~ H[13] = 0, H[14] = 1 - j, H[15] = 3 + 3j若设r=1,试计算H(=)并画出实系数形式的型结构。解:由式(7-16),可得1- 2~16121-j-3+ i-3-j1+jH(=)1Wiel4,-I161Wit'--11-W2-11Wi6152[1-2--15= W-(16-1)W-14=W-(16-2)=W,将上式化为实系数表示式=Wl利用W1616h7172元2元4元471~16+[6cos()+2sin(2-[2cos(1- 2-161216166H(2)162元、4元-1-2cos(1-2cos1616由此可画出实系数频率取样型结构,如下图所示
7.6 习题 5 ] 2 1 2 [ N − ( ) H 2 1 H z N− x[k] y[k] 1/N z −1 −r N z −N r 2H[1] 2H[2] H1 (z) H2 (z) H[0] (a) N 为偶数时修正的频率取样型结构图 2 − r ) 2π cos( [ ] N m − r m − cos([m]) ) 2π 2 cos( N m r z −1 z −1 (b) 实系数二阶子系统 Hm(z) 的结构图 7-7. 已知 FIR 数字滤波器频率特性的 16 个取样值为 [3] ~ [13] 0, [14] 1 j, [15] 3 3j [0] 12, [1] 3 j, [2] 1 j, = = − = − + = = − − = + H H H H H H H 若设 r=1,试计算 H(z)并画出实系数形式的型结构。 解: 由式(7-16),可得 − − + + − − + − + + − − − + − − = − − − − − − − − − − 1 5 1 1 6 1 4 1 1 6 2 1 1 6 1 1 1 6 1 1 6 1 3 j 1 1 j 1 1 j 1 3 j 1 12 16 1 ( ) z W z W z W z W z z H z 利用 1 16 (16 1) 16 15 W16 =W =W − − − , 2 16 (16 2) 16 14 W16 =W =W − − − ,将上式化为实系数表示式 − + − + + − + − + + + − − = − − − − − − − − 1 2 1 1 2 1 1 1 6 ) 16 4π 1 2cos( )] 16 4π ) 2sin( 16 4π 2 [2cos( ) 16 2π 1 2cos( )] 16 2π ) 2sin( 16 2π 6 [6cos( 1 12 16 1 ( ) z z z z z z z z H z 由此可画出实系数频率取样型结构,如下图所示