
82第1章离散信号与系统分析基础1-20如果[kl是一个周期为N的序列,它也是周期为2N的周期序列。令X[m]=DFS([k]周期为N,而X,[m]=DFS([k])周期为2N,试根据X,[m]来确定X,[m]。六22X,[mWmx[m解法1:x[K]=-1X,[2m]=2X,[m];m=0,1,.,N-1X,[2m+1]=0:m=0,1.,N-][ +[解法2:,[m]-2-[kJ=N'[+NW)m-EN[KJW +E[2X,[m/2]m为偶=(1+(-1)")[KW m为奇10试求出下列序列的DTFT1-21(1) x[K]=α'u[K] [a|<1(2) x[k]=α"u[-k] [α| >1[α[K|≤M(4) x[K]=α*u[k+3] [α|<1(3) x[K]=其它0(sin(pk/3)sin(pk/4)(5) x,[K]=Z (1/4)*8[k-3m](6) x[k] =pkpk11oαke-jkr解:(1)X,(ej)=(2) X, (ej0)1-αe-jn1-α"ejnMMMMoke-jkoo-jkkojko-jk=1+(3) X, (ej2+Ak=lk=ikl2 α'e-) =2Re(Z α'e-)-1=1+2Re()= 2 1-α cosQ -α * cos[(M +1)2]+ cos(M2)1-2αcosQ+α?_ 1-α2 - 2α** cos[(M +1)2]+2α M+2 cos(M2)1-2αcos2+α2α~e130(4)X,(ej )= DTFT(α~x,[+3]) =1-ae-jn(5) x,[k]=E (1/4)3"S[k-3n]
82 第 1 章 离散信号与系统分析基础 1-20 如 果 [ ] ~x k 是一个周期为 N 的序列 , 它也是周期为 2N 的周期序列。 令 [ ] = ~ X1 m [ ]} ~ DFS{x k 周期为 N,而 [ ] = ~ X2 m [ ]} ~ DFS{x k 周期为 2N,试根据 [ ] ~ X1 m 来确定 [ ] ~ X2 m 。 解法 1: mk N m N X m W N x k - =< > = å [ ] 1 ~ [ ] ~ 1 mk N m N X m W N 2 1 2 [ ] ~ 2 2 1 - =< > = å [ ]; 0,1, , 1 ~ [2 ] 2 ~ X 2 m = X1 m m = L N - [2 1] 0; 0,1, , 1 ~ X 2 m + = m = L N - 解法 2: å - = = 2 1 0 2 2 [ ] ~ [ ] ~ N k km W N X m x k å - = = 1 0 2 [ ] N ~ k km W N x k å - = + 2 1 2 [ ] N ~ k N km W N x k å - = = 1 0 2 [ ] N ~ k km W N x k å - = + + + 1 0 ( ) 2 [ ] N ~ k k N m N W N x k å - = = + - 1 0 2 [ ] ~ (1 ( 1) ) N k km N m x k W î í ì = 为奇 为偶 m X m m 0 2 [ / 2] 1 1-21 试求出下列序列的 DTFT (1) [ ] [ ] 1 x1 k = a u k a < k (2) [ ] [ ] 1 x2 k = a u -k a > k (3) î í ì £ = 0 其它 [ ] 3 k M x k k a (4) [ ] [ 3] 1 x4 k = a u k + a < k (5) [ ] (1/ 4) [ 3 ] 0 5 x k k n k n = å - ¥ = d (6) ÷ ø ö ç è æ ÷ ø ö ç è æ = k k k k x k p sin(p / 4) p sin(p / 3) [ ] 6 解:(1) å ¥ = - - - = = 1 0 1 1 ( ) k j j k jk e X e e W W W a a (2) W W a j j e X e 1 2 1 1 ( ) - - = (3) - - W - =- - W = W = +å + å k jk M k k jk M k j X e a e a e 1 1 3 ( ) 1 W = - W = = +å +å k jk M k k jk M k a e a e 1 1 1 1 2Re{ } 1 W a k jk M k e - = = + å 2Re{ } 1 0 = - - = å W a k jk M k e 1 1 2 cos 1 cos cos[( 1) ] cos( ) 2 2 1 2 - - + - - + + = + + a W a a W a M W a MW M M 2 2 1 2 1 2 cos 1 2 cos[( 1) ] 2 cos( ) a W a a a W a W - + - - + + = + + M M M M (4) W W W a a a j j j e e X e x k - - - - = + = 1 ( ) DTFT{ [ 3]} 3 3 1 3 4 (5) [ ] (1/ 4) [ 3 ] 3 5 0 x k k n n n = å - ¥ = d
831X,(e°)=Em(1/4)3"e-j3m21-(1/4)°e-j32(6) x.[k]=(1/12)Sa(pk/3)Sa(pk/4)由于DTFT(Sa(2.k))=(元/2.)P20(2)(P2。(2)表示幅度为1宽度为22周期为2元矩形波)故DTFT(Sa(元k/3))=3p2/3(2),DTFT(Sa(元k/4))=4p/2(2)X,(el)=一pax) (2)*Pxi2(2)2元4 P2元 /3(2)4 P元/2(2)?72元元2元一元-2元-元元元元4433Xe(ej°)=1/40≤2≤元/12元/12≤Q≤7元/12X(ej2)=[元/3-(—元/4+2)1/2元=(7元/12-2)/2元由对称性:[1/ 4[2|≤元/12元/12≤2≤7元/12X。(ej°)=3(7元/12-2)/2元07元/12≤2|≤元AXe(ejn)1/4Q元1元7元12121-22试确定下列序列的DTFT(1[A|≤ N[1-|k|/N[K]≤ N(1) y.[K]=(2) y,[k]=lo其它10其他[cos(kp/2N)[K|≤N(3) y,[k] =其他0e-j(N+)0e-j(N+0.5)QeXN+0.5)0evQsin[(N +0.5)2]io解:(1)Y,(ejn)=1-e-ine-j/2ej012sin(Q/2)K=-N
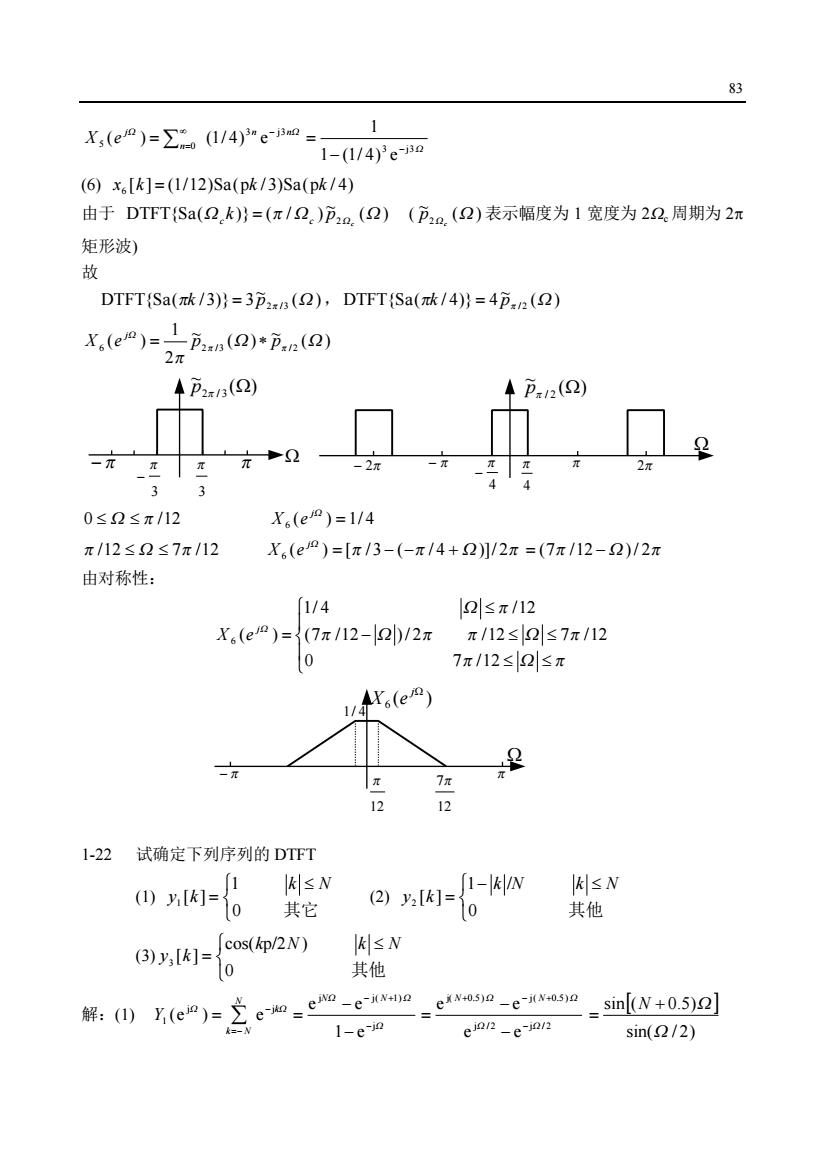
83 W n nW n j X e 3 j3 5 0 ( ) (1/ 4) e ¥ - å = = 3 j3W 1 (1/ 4) e 1 - - = (6) [ ] (1/12)Sa(p / 3)Sa(p / 4) 6 x k = k k 由于 ( ) ~ DTFT{Sa( )} ( / ) Wc k = p Wc p2Wc W ( ( ) ~p2Wc W 表示幅度为 1 宽度为 2Wc 周期为 2p 矩形波) 故 ( ) ~ DTFT{Sa( / 3)} 3 pk = p2p /3 W , ( ) ~ DTFT{Sa( / 4)} 4 pk = pp / 2 W ( ) ~ ( ) ~ 2 1 ( ) 6 2 /3 W / 2 W p p p W X e p p j = * ( ) ~p2p / 3 W - p p W 3 p - 3 p ( ) ~pp / 2 W W - 2p - p p 2p 4 p - 4 p 0 £ W £ p /12 ( ) 1/ 4 6 = jW X e p /12 £ W £ 7p /12 p p W p W ( ) [ /3 ( / 4 )]/ 2 6 = - - + j X e = (7p /12 - W )/ 2p 由对称性: ï î ï í ì £ £ - £ £ £ = p W p p W p p W p W p W 0 7 /12 (7 /12 )/ 2 /12 7 /12 1/ 4 /12 ( ) 6 j X e W - p p ( ) 6 jW X e 12 p 12 7p 1/ 4 1-22 试确定下列序列的 DTFT (1) î í ì £ = 0 其它 1 [ ] 1 k N y k (2) î í ì - £ = 0 其他 1 / [ ] 2 k N k N y k (3) î í ì £ = 0 其他 cos( p/2 ) [ ] 3 k N k N y k 解:(1) W kW N k N Y j j 1 (e ) e - =- = å W W W j j j( 1) 1 e e e - - + - - = N N j / 2 j / 2 j( 0.5) j( 0.5) e e e e W W W W - + - + - - = N N [ ] sin( / 2) sin ( 0.5) W + W = N