
第3章随机向量及其分布3.1二维随机变量的概率分布教学内容:教材46-50页,主要内容:二维随机变量的定义、分布函数及其性质。二维离散型随机变量的分布列及性质、二维连续型随机变量的密度函数,性质及概率计算。教学目的:(1)理解二维随机变量的实际意义,理解二维随机变量分布函数的意义,掌握二维随机变量分布函数的性质:(2)熟练掌握二维离散型随机变量的定义,分布列的表示方法和性质,掌握二维离散型随机变量分布列的一般求解过程;(3)理解二维连续型随机变量分布密度函数的意义及性质,掌握由密度函数求概率的计算方法:(4)了解二维均匀分布。教学的过程和要求:一。二维随机变量的引入(利用生活中的例子,如书中本章引言部分的例子或其它)。二维随机变量的引入:在很多实际问题中,试验结果需要用两个或两个以上的随机变量才能描述,而且这些随机变量之间往往都有一定的联系,例如:研究儿童的生长发育状况,儿童的身高X和体重Y是两个随机变量,并且X与Y之间又有一定的相关性因而我们有必要将X、Y放在一起作为一个整体进行研究,并将(X,Y)称为二维随机变量。下面给出二维随机变量的具体定义定义:设Q=(0)为样本空间,X=X(0)和Y=Y(o)是定义在Q上的随机变量,则由它们构成的一个二维向量(X,Y)称为二维随机变量(或二维随机向量)。二。对比一维随机变量分布函数的定义给出二维随机变量分布函数的定义及性质;画出二维随机变量取值范围的图形,帮助理解分布函数的意义;3.1.1二维随机变量分布函数:1.定义:设(X,Y)是二维随机变量,对于任意实数x、y,称二元函数F(x,y)=p(X≤x,Y≤y)为二维随机变量(X,Y)的分布函数或随机变量X与Y的联合分布函数,它表示随机事件(X≤x)与(Y≤同时发生的概率,2.定理:分布函数F(x,y)具有下列性质:1°(有界性)对于任意实数x,y,都有
第 3 章 随机向量及其分布 3.1 二维随机变量的概率分布 教学内容:教材 46-50 页,主要内容:二维随机变量的定义、分布函数及其性质。 二维离散型随机变量的分布列及性质、二维连续型随机变量的密度函数,性质及 概率计算。 教学目的: (1)理解二维随机变量的实际意义,理解二维随机变量分布函数的意义,掌握 二维随机变量分布函数的性质; (2)熟练掌握二维离散型随机变量的定义,分布列的表示方法和性质,掌握二 维离散型随机变量分布列的一般求解过程; (3)理解二维连续型随机变量分布密度函数的意义及性质,掌握由密度函数求 概率的计算方法; (4)了解二维均匀分布。 教学的过程和要求: 一. 二维随机变量的引入(利用生活中的例子,如书中本章引言部分的例子或 其它)。 二维随机变量的引入: 在很多实际问题中,试验结果需要用两个或两个以上的随机变量才能描述, 而且这些随机变量之间往往都有一定的联系. 例如:研究儿童的生长发育状况, 儿童的身高 X 和体重 Y 是两个随机变量,并且 X 与 Y 之间又有一定的相关性. 因 而我们有必要将 X、Y 放在一起作为一个整体进行研究,并将(X,Y) 称为二维随 机变量。下面给出二维随机变量的具体定义 定义:设W = {w} 为样本空间, X X = {w} 和Y Y = {w}是定义在W 上的随机 变量,则由它们构成的一个二维向量 ( X Y, ) 称为二维随机变量(或二维随机向 量)。 二. 对比一维随机变量分布函数的定义给出二维随机变量分布函数的定义及性 质;画出二维随机变量取值范围的图形,帮助理解分布函数的意义; 3.1.1 二维随机变量分布函数: 1.定义:设(X,Y) 是二维随机变量,对于任意实数 x、y,称二元函数 F(x,y) = p{X £ x,Y £ y} 为二维随机变量(X,Y) 的分布函数或随机变量 X 与 Y 的联合分布函数,它表示随 机事件{X £ x}与{Y £ y}同时发生的概率. 2.定理:分布函数F(x, y) 具有下列性质: o 1 (有界性)对于任意实数 x, y ,都有
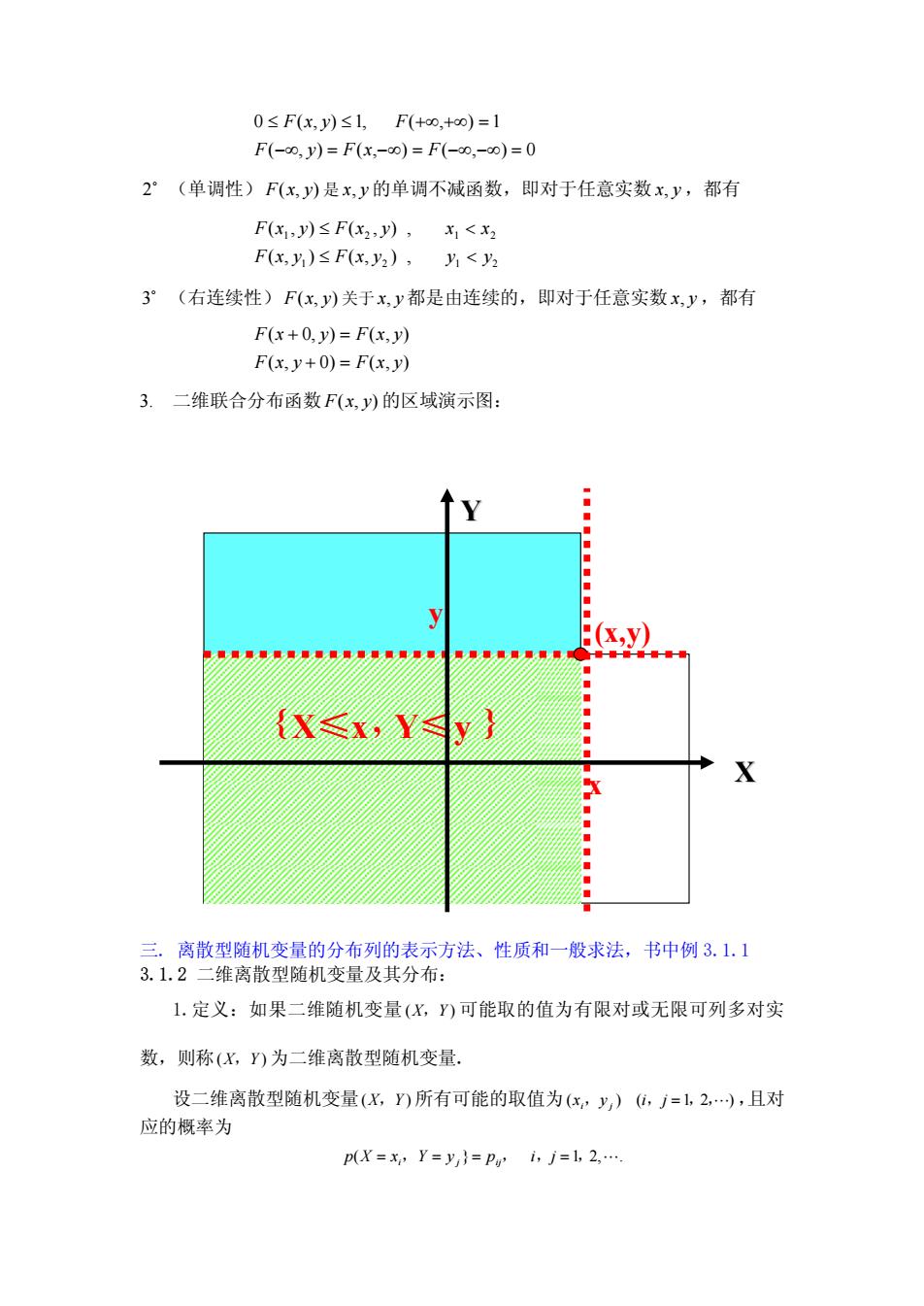
0≤F(x,y)≤1,F(+00,+0) = 1F(-00, y) = F(x,-00) = F(-00,-00) = 02°(单调性)F(xy)是x,y的单调不减函数,即对于任意实数x,y,都有F(x,J)≤F(x2,y),X<X2F(x,y)≤F(x,y2) ,yi<y23°(右连续性)F(x,J)关于xy都是由连续的,即对于任意实数x,y,都有F(x+0,y)= F(x,y)F(x, y+ 0)= F(x,y)3.二维联合分布函数F(x,y)的区域演示图:Y..:(x,y)XAXYX三.离散型随机变量的分布列的表示方法、性质和一般求法,书中例3.1.13.1.2二维离散型随机变量及其分布:1.定义:如果二维随机变量(X,Y)可能取的值为有限对或无限可列多对实数,则称(X,Y)为二维离散型随机变量设二维离散型随机变量(X,Y)所有可能的取值为(x,y)(i,j=1,2,),且对应的概率为p(X=x, Y=y,)=pyi, j=l, 2
( , ) ( , ) ( , ) 0 0 ( , ) 1, ( , ) 1 -¥ = -¥ = -¥ -¥ = £ £ +¥ +¥ = F y F x F F x y F o 2 (单调性) F(x, y) 是 x, y 的单调不减函数,即对于任意实数 x, y ,都有 1 2 1 2 1 2 1 2 ( , ) ( , ) , ( , ) ( , ) , F x y F x y y y F x y F x y x x £ < £ < o 3 (右连续性) F(x, y) 关于 x, y 都是由连续的,即对于任意实数 x, y ,都有 ( , 0) ( , ) ( 0, ) ( , ) F x y F x y F x y F x y + = + = 3. 二维联合分布函数F(x, y) 的区域演示图: 三. 离散型随机变量的分布列的表示方法、性质和一般求法,书中例 3.1.1 3.1.2 二维离散型随机变量及其分布: 1.定义:如果二维随机变量 (X,Y) 可能取的值为有限对或无限可列多对实 数,则称(X,Y) 为二维离散型随机变量. 设二维离散型随机变量(X,Y) 所有可能的取值为(x ,y ) (i,j =1,2,L) i j ,且对 应的概率为 p(X = x ,Y = y } = p , i,j =1,2,L. i j ij X Y x y { X≤x , } Y≤y (x,y)

则称上式为二维随机变量(X,Y)的概率分布或X与Y的联合概率分布:也常用表格表示如表3.1表3.1V片J2X............xPuPi2PuX2.....P21PnPaj1三主主......*.....xPtPizPy::::..........2.二维离散型随机变量的分布列的性质:r2)1)pu≥0,i, j=1, 2,.*.ZPy =1=3.二维离散型随机变量的分布列的求法:例3.1.1设随机变量X在1,2,3,4中等可能的取值,另一个随机变量Y在1~X中等可能地取一整数值,求(X,Y)的分布律。解:由乘法公式容易求得(X,Y)的分布律为P(X =i,Y = j) = P(X =i) = P(X =i,Y = j)1 147(X,Y)的联合概率分布用表格形式即为表3.2表3.2Y1234X1000141100288111031212121111416161616
则称上式为二维随机变量(X,Y) 的概率分布或X与Y的联合概率分布. 也常用表 格表示如表 3.1 表 3.1 Y X 1 y 2 y . j y . 1 x 11 p 12 p . j p1 . 2 x 21 p 22 p . j p2 . M M M . M . i x i 1 p i2 p . ij p . M M M . M . 2.二维离散型随机变量的分布列的性质: 1) pij ³ 0,i,j =1, 2,L. 2)åå +¥ = +¥ = = 1 1 1 i j ij p 3.二维离散型随机变量的分布列的求法: 例 3.1.1 设随机变量 X 在 1,2,3,4 中等可能的取值,另一个随机变量Y 在1 ~ X 中等可能地取一整数值,求(X,Y)的分布律。 解:由乘法公式容易求得(X,Y) 的分布律为 i P X i Y j P X i P X i Y j 1 4 1 { , } { } { , } = × = = = = = = = (X,Y) 的联合概率分布用表格形式即为表 3.2 表 3.2 Y X 1 2 3 4 1 4 1 0 0 0 2 8 1 8 1 0 0 3 12 1 12 1 12 1 0 4 16 1 16 1 16 1 16 1

四.对比一维随机变量给出二维随机变量的密度函数,着重说明密度函数的性质及其在求概率中的应用,并举例3.1.2。3.1.3二维连续型随机变量及其分布:1.定义:设二维随机变量(X,Y)的分布函数为F(x,J),如果存在非负可积的二元函数f(x,y),使得对任意实数x、y,有F(x, y)= [m[f(x、y)dxd)则称(X,Y)为二维连续型随机变量,称函数F(x,J)为二维随机变量(X,Y)的分布密度函数或概率分布密度或随机变量X和Y的联合分布密度函数。同时称相应的分布为连续分布。2.定理3.1.2对于二维连续型随机变量(X,Y)的分布密度f(x,y)和分布函数F(x,J)具有下列性质:1°在整个二维平面上f(x,y)满足f(x,J)≥0, (x<+0,以<+80)[ f(x, y)dxdy =12°在整个二维平面上F(x,y)连续,在F(x,J)已知时,可通过求二阶混合偏导"F(在它的连续点处)获得密度函数:axoyT(,)=o"Faxay3°对任意的平面区域G,有P(X,Y)eG)= [[f(x, y)dxdyG3.二维连续型随机变量的计算:例3.1.2设二维随机变量(X,Y)的分布密度Ae-(2x+y)。x>0,y>0f(x,)0,其他求系数A与(X,Y)的分布函数F(x,y)以及概率P(Y≤X)。解:由
四. 对比一维随机变量给出二维随机变量的密度函数,着重说明密度函数的性质 及其在求概率中的应用,并举例 3.1.2。 3.1.3 二维连续型随机变量及其分布: 1.定义:设二维随机变量(X,Y) 的分布函数为 F(x,y) ,如果存在非负可积的二 元函数 f (x,y) ,使得对任意实数 x、y,有 ò ò -¥ -¥ = x y F(x,y) f (x、y)dxdy 则称(X,Y) 为二维连续型随机变量,称函数 f (x,y) 为二维随机变量(X,Y) 的分 布密度函数或概率分布密度或随机变量X和Y的联合分布密度函数. 同时称相应 的分布为连续分布。 2.定理 3.1.2 对于二维连续型随机变量( X Y, ) 的分布密度 f (x, y)和分布函数 F(x, y) 具有下列性质: o 1 在整个二维平面上 f (x, y)满足 ( ) ïþ ï ý ü = ³ < +¥ < +¥ ò ò +¥ -¥ +¥ -¥ ( , ) 1 ( , ) 0, , f x y dxdy f x y x y o 2 在整个二维平面上 F(x, y) 连续,在 F(x, y) 已知时,可通过求二阶混合偏导 x y F ¶ ¶ ¶ 2 (在它的连续点处)获得密度函数: ( ) x y F f x y ¶ ¶ ¶ = 2 , o 3 对任意的平面区域G ,有 {( ) } ( ) òò Î = G P X,Y G f x, y dxdy 3.二维连续型随机变量的计算: 例 3.1.2 设二维随机变量( X Y, )的分布密度 ( ) ( ) î í ì > > = - + 0, 其他 , 0, 0 , 2 Ae x y f x y x y 求系数 A 与(X ,Y )的分布函数 F(x, y) 以及概率 P{Y £ X}。 解:由

1- f(x,)dxdy= Ae-2+)dxdy=知A=2,故(X,Y)的分布密度J2e-(2x+), x>0,y>0f(x,y):其他0,对f(xy)积分即知(X,Y)的分布函数为F(x, y)= J" " (x、)dxdy["2e-2*dxf'e-'dy ,x > 0, y>0[o,其他[({-e-2*)1-e"), x>0,y>0其他[0,概率PX)为P(≤x)= J[2e-(2+)dxdy= " 2e-*dxf"e-'dy0VJ"2e-(i-e yx = }五.对比一维均匀分布,给出二维均勺分布的密度函数,举例3.1.3说明其应用1.二维均匀分布:定义:(二维均勾分布)设平面区域D的面积为A>0,若二维随机变量(X,Y)具有密度函数[1(x,J)eDf(x,y)=A[o,(x,y)& D则称(X,Y)服从区域D上的二维均匀分布2.二维均匀分布的应用:例3.1.3:设国际市场上甲、乙两种产品的需求量(单位:吨)是服从区域G上的均匀分布,G=((x,y)2000<x≤4000,3000y≤6000),试求两种产品需求量的差建不超过1000吨的概率.m解:设甲、乙两产品的需求量分别是X和Y,则
( ) ò ò ò ò +¥ +¥ - + +¥ -¥ +¥ -¥ = = = 0 0 2 2 1 ( , ) A f x y dxdy Ae dxdy x y 知 A = 2 ,故( X Y, )的分布密度 ( ) ( ) î í ì > > = - + 0, 其他 2 , 0, 0 , 2 e x y f x y x y 对 f (x, y)积分即知(X ,Y )的分布函数为 ò ò -¥ -¥ = x y F(x,y) f (x、y)dxdy ïî ï í ì > > = ò ò - - 0, 其他 2 , 0, 0 0 0 2 e dx e dy x y x y x y ( )( ) î í ì - - > > = - - 0, 其他 1 1 , 0, 0 2 e e x y x y 概率 P{Y £ X}为 { } ( ) ( ) 3 1 2 1 2 2 0 2 0 0 2 0 2 = - = £ = = ò òò ò ò +¥ - - +¥ - - < £ - + e e dx P Y X e dxdy e dx e dy x x x x y y x x y 五. 对比一维均匀分布,给出二维均匀分布的密度函数,举例 3.1.3 说明其应用 1.二维均匀分布: 定义:(二维均匀分布)设平面区域 D 的面积为 A > 0,若二维随机变量(X,Y) 具有密度函数 ï î ï í ì Ï Î = x y D x y D f x y A 0, ( , ) , ( , ) 1 ( , ) 则称(X,Y) 服从区域 D 上的二维均匀分布. 2.二维均匀分布的应用: 例 3.1.3:设国际市场上甲、乙两种产品的需求量(单位:吨)是服从区域G 上 的均匀分布,G ={(x, y) 2000 < x £ 4000 , 3000 < y £ 6000},试求两种产品需求量的差 不超过 1000 吨的概率. 解:设甲、乙两产品的需求量分别是 X 和Y ,则