
第1章随机事件与概率内容:基本概念,古典概型,几何概型,条件概率,事件的独立性重点:1.基本概念:样本空间,随机事件,随机事件的运算2.古典概型的概率计算3.条件概率与事件的独立性,自然界和社会上发生的现象按其发生的特点可分为:必然现象,随机现象。必然现象:在一定的条件下所发生的结果具有确定性随机现象:在一定的条件下所发生的结果具有不确定性,且满足以下四个特点。1.全部结果的可预知性2.每次结果的不可预知性,3.试验的可重复性,4.大量重复试验的结果呈规律性概率论是研究和揭示随机现象统计规律性的一门数学学科。1.1样本空间与随机事件一.样本空间与随机事件随机实验举例:E:将一枚硬币上抛两次,观察其正反面的出现的情况。Ez:将一枚硬币上抛两次,观察正面出现的次数。Es:袋中有10只白球,2只红球,任取一只观察其颜色。E4:抛一颗般子,观察出现的点数Es:某商场每星期一上午10点至12点来商场的人数N.Es:某城市8月份的平均气温T.E:测量某工件的长度E:在一批灯泡中任意抽取一个,测试它的寿命x.样本空间:随机试验E的所有可能发生的结果の的集合.记:Q=(の),の:称样本点.以上各试验的样本空间分别为:Q,=(正正,正反,反正,反反】2,=(0,1,2]Q3=(红色,白色)Q=(1,2,3,4,5,6)Q,={0,1,2,3,]Q={T /28°C≤T≤37℃)Q,=[测量值L110.5cm≤L≤11.5cmαg=(x / x≥0(小时))注:样本空间的元素是由试验的目的和内容确定的.如:E,与E试验的Q与2例1:设试验为从装有三个白球(记为1,2,3,号)与两个黑球(记为4,5号)的袋中任取两个球,1
1 第 1 章 随机事件与概率 内容: 基本概念,古典概型,几何概型,条件概率,事件的独立性. 重点:1. 基本概念:样本空间,随机事件,随机事件的运算. 2. 古典概型的概率计算. 3.条件概率与事件的独立性. 自然界和社会上发生的现象按其发生的特点可分为:必然现象,随机现象。 必然现象:在一定的条件下所发生的结果具有确定性. 随机现象:在一定的条件下所发生的结果具有不确定性,且满足以下四个特点. 1.全部结果的可预知性 2.每次结果的不可预知性. 3.试验的可重复性. 4.大量重复试验的结果呈规律性. 概率论是研究和揭示随机现象统计规律性的一门数学学科。 1.1 样本空间与随机事件 一.样本空间与随机事件 随机实验举例: E1: 将一枚硬币上抛两次,观察其正反面的出现的情况。 E2:将一枚硬币上抛两次,观察正面出现的次数。 E3:袋中有 10 只白球,2 只红球,任取一只观察其颜色。 E4: 抛一颗骰子,观察出现的点数. E5: 某商场每星期一上午 10 点至 12 点来商场的人数 N. E6: 某城市 8 月份的平均气温 T. E7:测量某工件的长度. E8:在一批灯泡中任意抽取一个,测试它的寿命 x. 样本空间:随机试验 E 的所有可能发生的结果ω的集合.记:Ω={ω},ω:称样 本点. 以上各试验的样本空间分别为: Ω1={正正,正反,反正,反反} Ω2={0,1,2} Ω3={红色,白色} Ω4={1,2,3,4,5,6} Ω5={0,1,2,3,.} Ω6={T∣280 C≤T≤370 C} Ω7 ={测量值 L∣10.5cm≤L≤11.5cm} Ω8={x∣x≥0(小时)} 注:样本空间的元素是由试验的目的和内容确定的.如:E1与 E2试验的Ω1与Ω2. 例 1:设试验为从装有三个白球(记为 1,2,3,号)与两个黑球(记为 4,5 号)的袋中任取两个球

(a)如果观察取出的两个球的颜色,则样本空间是由3个样本点构成的集合Q,=两个白球,两个黑球,一白一黑(b)如果观察取出的两个球的号码,则样本空间是由10个样本点构成的集合Q2=[012,13,014,15,023,024,025,034,035,045]其中:の是2的样本点,表示“取出的是第i号球和第j号球”随机事件:随机试验E的样本空间2的任意一个子集称为E的随机事件.用A,B,C,…表示,简称事件.基本事件:只有一个样本点的集合,必然事件:集合9.不可能事件:空集Φ。注:A发生当且仅当A中的一个样本点出现例如:E:A表示至少出现一次正面.则A=(正正,正反,反正)E:B表示点数不小于3.则B=[3,4,5,6)12E:C表示灯泡的使用寿命不超过1000小时.则C=[x|0≤x≤1000二.事件间的关系与运算1.包含关系AcB:A发生则B必发生2.相等关系A=B:A发生则B必发生且B发生则A必发生3.A与B事件的和事件AUB=(x|xEA或xEB):A事件与B事件至少有一个发生推广:[UJA,称n个事件的和事件UJA,称可列个事件的和事件,4.A与B事件的积事件ANB=xxEA且xeB}:A事件与B事件同时发生推广:n4,称n个事件的积事件,「n4,称可列个事件的积事件.5.A与B事件的差A-B=/xxEA但x@B/:A发生而B不发生6.A与B互不相容(互斥):若ANB=Φ.此时记AUB为:A+B(A与B的直和)A与B不相容当且仅当A与B不能同时发生n个两两互不相容的事件A,A…,A,即为其中任意两个事件A,与A,(i+j)为互不相容事件.此时可记UA.为:A+A,+.+A,k=l7.A与B互为对立事件(逆事件):若ANB=Φ且AUJB=Q.记:A的对立事件为:A2
2 (a) 如果观察取出的两个球的颜色,则样本空间是由 3 个样本点构成的集 合 Ω1 ={两个白球,两个黑球,一白一黑} (b) 如果观察取出的两个球的号码,则样本空间是由 10 个样本点构成的 集合 Ω2 ={ω12,ω13,ω14,ω15,ω23,ω24,ω25,ω34,ω35,ω45} 其中:ωij是Ωb的样本点,表示“取出的是第 i 号球和第 j 号球”. 随机事件:随机试验E的样本空间Ω的任意一个子集称为E的随机事件.用A,B,C,. 表示,简称事件. 基本事件:只有一个样本点的集合. 必然事件:集合Ω. 不可能事件:空集ф. 注: A 发生 当且仅当 A 中的一个样本点出现. 例如:E1:A 表示至少出现一次正面.则 A={正正,正反,反正} E4:B 表示点数不小于 3. 则 B={3,4,5,6}ω12 E8: C 表示灯泡的使用寿命不超过 1000 小时.则 C={x∣0≤x≤1000} 二.事件间的关系与运算 1.包含关系 AÌ B:A 发生则 B 必发生. 2.相等关系 A=B: A 发生则 B 必发生且 B 发生则 A 必发生. 3. A 与 B 事件的和事件 AU B={x∣xÎA 或 xÎB}:A 事件与 B 事件至少有一个 发生. 推广: 1 1 n k k k k A A ¥ = = U U 称n个事件的和事件, 称可列个事件的和事件 . 4.A 与 B 事件的积事件 AI B = { x xÎ Î A且 x B } :A 事件与 B 事件同时发生. 推广: 1 1 n k k k k A A ¥ = = I I 称n个事件的积事件, 称可列个事件的积事件. 5. A 与 B 事件的差 A- B = { x xÎ Ï A 但x B }:A 发生而 B 不发生. 6.A 与 B 互不相容(互斥):若 A B I = f.此时记 AU B 为:A+B(A 与 B 的直和) A 与 B 不相容当且仅当 A 与 B 不能同时发生. 1 2 n n 1 2 k= A n i j n n A ,A ,.,A A A (i j ) A A . A ¹ U + + + 1 个两两互不相容的事件 即为其中任意两个事件 与 为互不相容事件.此时可记 为: 7.A 与 B 互为对立事件(逆事件):若 AI B = f且 AUB . = W 记:A 的对立事 件为: A

(2) A=A可见:(1)若A=B,则:B=A(3)Φ=2, =Φ图1.A与B不相容图2.A与B互为对立事件例2.设A和A分别表示在例1(b)中“1号球出现“和”2号球出现“的事件,则有A, =[012,013,014015]A, =[012,023,024,025]且: AUA, =[012, 013,014015,023,024025/, ANA, =/012]AUA = [034,035,045]A -A =[013,04015],事件间的运算关系完全等同与集合的运算关系,因此事件间的运算规律完全等同与集合的运算规律.运算规律:(1)交换律:AUB=BUA,ANB=BNA(2)结合律:AU(BUC)=(AUBUC,AN(BNC)=(ANB)NC(3)分配律:A(BUC)=ABUAC,AU(BNC)=(AUB)N(AUC)(4)对偶律:AUB=BNA,ANB=BUA例3.在如图所示的电路中,设事件A,B,C分别表示继电器接点a,b,闭合,事件D表示指示灯d亮,则由电路是否闭合立刻可知这四个事件之间有如下关系:D=A(BUC),D=AUBUC=AUBC,AD=Φm3
3 可见:(1)若 A =B,则: B A = (2) A A = (3)f = W, W = f 图 1.A 与 B 不相容 图 2. A 与 B 互为对立事件 例2. 设 A1和 A2分别表示在例 1(b)中“1 号球出现“和”2 号球出现“的事件, 则有 1 12 13 14 15 2 12 23 24 25 1 2 12 13 14 15 23 24 25 1 2 12 1 2 13 14 15 1 2 34 35 45 A { , , } A { , , , } A A { , , , , } , A A { } A A { , }, A A { , , } = w w w w = w www = w w w w w w w = w - = w w w = www U I U 且: 事件间的运算关系完全等同与集合的运算关系,因此事件间的运算规律完全等同 与集合的运算规律. 运算规律:(1)交换律: AU B B = = U A, AI I BBA (2)结合律: AU( B UC ) = = ( AU B )UC, AI( B IC ) ( AI I B ) C (3)分配律: A( B UC ) = = AB U AC, AU( B IC ) ( AU B )I U ( A C ) (4)对偶律: AU B = = B I A, AI U B B A 例 3.在如图所示的电路中,设事件 A,B,C 分别表示继 电器接点 a,b,c 闭合,事件 D 表示指示灯 d 亮,则由电 路是否闭合立刻可知这四个事件之间有如下关系: D = A( B UC ) , D = AU B U U C =A BC , AD = f
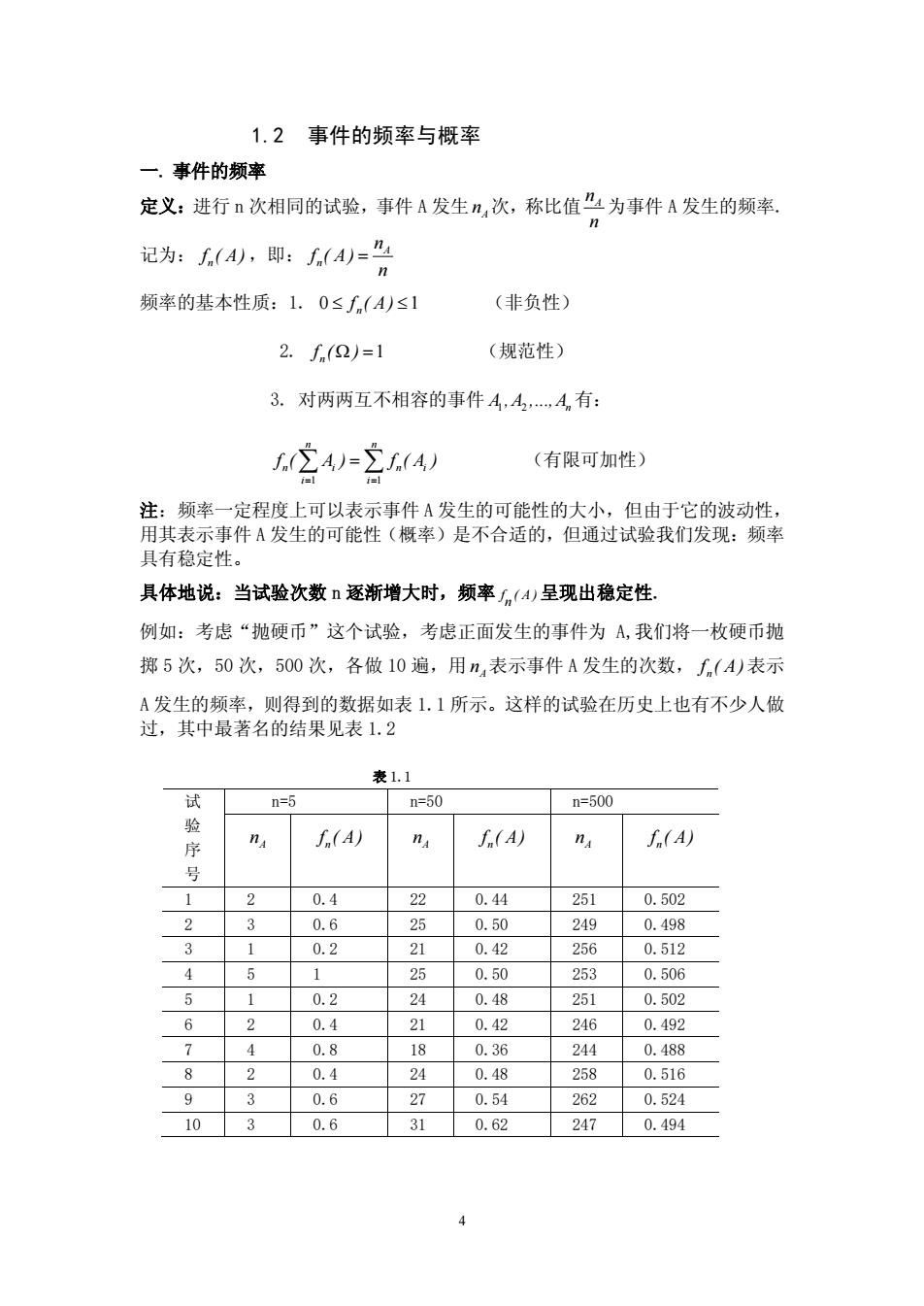
1.2事件的频率与概率一.事件的频率定义:进行n次相同的试验,事件A发生n,次,称比值"4为事件A发生的频率。n记为:J.(A),即:J,(A)="4n(非负性)频率的基本性质:1.0≤f(A)≤12. J,(Q)=1(规范性)3.对两两互不相容的事件A,A..A有:Zf(A,)f.(ZA)=)(有限可加性)=注:频率一定程度上可以表示事件A发生的可能性的大小,但由于它的波动性,用其表示事件A发生的可能性(概率)是不合适的,但通过试验我们发现:频率具有稳定性。具体地说:当试验次数n逐渐增大时,频率(A)呈现出稳定性例如:考虑“抛硬币”这个试验,考虑正面发生的事件为A,我们将一枚硬币抛掷5次,50次,500次,各做10遍,用n,表示事件A发生的次数,J(A)表示A发生的频率,则得到的数据如表1.1所示。这样的试验在历史上也有不少人做过,其中最著名的结果见表1.2表1.1试n=5n=50n=500验J.(A)f.(A)naJ.(A)nnA序号210. 4220. 442510.502230.6250. 502490.498310. 2210. 422560.512451250.502530.50612450.20.482510.502620. 4210. 422460.492740.8180.362440. 488820. 4240.482580.51627930.60. 542620.5241030.6310.622470. 4944
4 1.2 事件的频率与概率 一. 事件的频率 定义:进行 n 次相同的试验,事件 A 发生 A n 次,称比值 A n n 为事件 A 发生的频率. 记为: n f ( A ),即: A n n f ( A ) n = 频率的基本性质:1. 0 1 n £ £ f ( A ) (非负性) 2. 1 n f ( ) W = (规范性) 3. 对两两互不相容的事件 A1 2 n ,A ,., A 有: 1 1 n n n i n i i i f ( A ) f ( A ) = = å å= (有限可加性) 注:频率一定程度上可以表示事件 A 发生的可能性的大小,但由于它的波动性, 用其表示事件 A 发生的可能性(概率)是不合适的,但通过试验我们发现:频率 具有稳定性。 具体地说:当试验次数 n 逐渐增大时,频率 f ( A ) n 呈现出稳定性. 例如:考虑“抛硬币”这个试验,考虑正面发生的事件为 A,我们将一枚硬币抛 掷 5 次,50 次,500 次,各做 10 遍,用 A n 表示事件 A 发生的次数, n f ( A )表示 A 发生的频率,则得到的数据如表 1.1 所示。这样的试验在历史上也有不少人做 过,其中最著名的结果见表 1.2 表 1.1 试 n=5 n=50 n=500 验 序 号 A n n f ( A ) A n n f ( A ) A n n f ( A ) 1 2 0.4 22 0.44 251 0.502 2 3 0.6 25 0.50 249 0.498 3 1 0.2 21 0.42 256 0.512 4 5 1 25 0.50 253 0.506 5 1 0.2 24 0.48 251 0.502 6 2 0.4 21 0.42 246 0.492 7 4 0.8 18 0.36 244 0.488 8 2 0.4 24 0.48 258 0.516 9 3 0.6 27 0.54 262 0.524 10 3 0.6 31 0.62 247 0.494

表1.2试验者f.(A)nnA德摩根204810610.5181蒲丰404020480.5069皮尔逊1200060190.5016皮尔逊24000120120.5005从试验中可以看出:当试验次数n逐渐增大时,A事件发生的频率越来越稳定在0.5数值周围.因此以0.5表示事件A发生的概率以上表达了概率的统计性的定义,但要从频率直接获得概率确实非常困难的,甚至是不可能的.但我们从中提炼出概率的基本性质,从而给出概率的定义,二。概率的公理化定义定义:设Q为试验E的样本空间,Q的子集A是随机事件,P(A)是实值函数,如果P(A)满足下述三条公理:1.(非负性)VA,有P(A)≥02.(规范性)对于必然事件2,有P(Q)=13.(完全可加性)对可列个两两互不相容的事件A,A.A...A..有:J.(ZA)-ZJ.(A)i=li=l则称P(A)为随机事件A的概率,记作P(A)三概率的性质1. P(Φ)= 0证明:由于Q=Q+++.+.且Q...两两互不相容则:P(Q)=P(Q)+P(Φ)+P(Φ)+..所以:P(Φ)+P(Φ)+P(Φ)+..=0,又P(Φ)≥0则得:P(Φ)=02.(有限可加性)对两两互不相容的事件A.,A...A有:PA)P(A)i=li=l证明:A=A+A+A+...+A,+Φ++...i=l且它们两两互不相容,则有:5
5 表 1.2 试验者 n A n n f ( A ) 德摩根 2048 1061 0.5181 蒲 丰 4040 2048 0.5069 皮尔逊 12000 6019 0.5016 皮尔逊 24000 12012 0.5005 从试验中可以看出:当试验次数 n 逐渐增大时,A 事件发生的频率越来越稳 定在 0.5 数值周围.因此以 0.5 表示事件 A 发生的概率. 以上表达了概率的统计性的定义,但要从频率直接获得概率确实非常困难的,甚 至是不可能的.但我们从中提炼出概率的基本性质,从而给出概率的定义. 二. 概率的公理化定义 定义:设W 为试验 E 的样本空间,W 的子集 A 是随机事件, P( A )是实值函数, 如果 P( A )满足下述三条公理: 2 3 k 1 1 1 P(A) 0 2. ( ) n i n i i i .( A, ,A ,A ,.,A ., : f ( A ) f ( A ) ( A) A , ¥ ¥ = = " ³ W W å å= 1 非负性) 有 规范性 对于必然事件 ,有P( )=1 3.(完全可加性)对可列个两两互不相容的事件A 有 则称P 为随机事件 的概率 记作P(A). 三. 概率的性质 1. P( ) f = 0 证明:由于 W = W + f + f + .+ . 且W,f f, ,. , 两两互不相容 0 0 0 : P( ) P( ) P( ) P( ) . : P( ) P( ) P( ) . , P( ) P( ) W = W + f + f + f + f + f + = f ³ f = 则 所以 又 则得: 2.(有限可加性)对两两互不相容的事件 A1 2 n ,A ,., A 有: 1 1 n n i i i i P( A ) P( A ) = = å å= 证明: 1 2 3 n åAi n = A + A + A + .+ A + f + f + . i=1 且它们两两互不相容,则有: