
第三章矩阵的运算 41 此线性变换的系数构成的m×矩阵为 21 l22 Ami Am2 。 称为线性变换的系数矩阵, 设两个线性变换 Jy=1k+12x2+013x3 (3-1) y2=421X1+422X2+423X3, x1=b41+b242, x2=b214+b2242, (3-2) X3=b3141+b3242
第三章 矩阵的运算 11 12 1 21 22 2 1 2 . . n n m m mn a a a a a a m n a a a 此线性变换的系数构成的 矩阵为 称为线性变换的系数矩阵 1 11 1 12 2 13 3 2 21 1 22 2 23 3 1 11 1 12 2 2 21 1 22 2 3 31 1 32 2 , (3 1) , , , (3 2) , y a x a x a x y a x a x a x x b t b t x b t b t x b t b t = + + − = + + = + = + − = + 设两个线性变换

第三章矩阵的运算 为求出从,t,到y,y,的线性变换,可将3-2)代入(3-1)得: Jy=(a4+ab+ag014+a:+a.5a+ab,6-3) y=(a21b1n+22b21+a23b31)41+(a2ib2+022b2+a2sb2)2 我们把线性变换3-3)叫做线性变换(3-1)与3 2)的乘积,相应地把3一3)所对应的矩阵定义为3一 1)与3-2)所对应的矩阵的乘积,即 b12 L12 013 22 L23 b31 b32 41b11+a1zb21+413b3141b12+41b2z+413b2 L21b1+42b21+423b31 a21b12+u22b22+023b32
第三章 矩阵的运算 1 2 1 2 11 11 12 21 13 31 1 11 12 12 22 13 32 2 21 11 22 21 23 31 1 21 12 22 22 23 32 2 , , (3 2) (3 1) ( ) ( ) , (3 3) ( ) ( ) . t t y y y a b a b a b t a b a b a b t y a b a b a b t a b a b a b t − − = + + + + + − = + + + + + 为求出从 到 的线性变换,可将 代入 得: 我们把线性变换(3-3)叫做线性变换(3-1)与(3- 2)的乘积,相应地把(3-3)所对应的矩阵定义为(3- 1)与(3-2)所对应的矩阵的乘积,即 11 12 11 12 13 21 22 21 22 23 31 32 11 11 12 21 13 31 11 12 12 22 13 32 21 11 22 21 23 31 21 12 22 22 23 32 b b a a a b b a a a b b a b a b a b a b a b a b a b a b a b a b a b a b + + + + = + + + +

第三章矩阵的运算 2.矩阵乘法的定义 定义3.1.3设A=(a)是一个m×s矩阵,B=(b) 是一个s×n矩阵,作m×矩阵C=(ci),其中 c与=a4,+ab,++abg=∑4abg 矩阵C称为矩阵A与矩阵B的乘积, 记作C=AB,即
第三章 矩阵的运算 1 1 2 2 1 ( ) , ( ) , ( ) 3.1.3 , ij ij ij s ij i j i j is sj ik kj k A a m s B b s n m n C c c a b a b a b a b C A B C AB = = = = = + + + = = 设 是 一 个 矩 阵 是 一 个 矩 阵 作 矩 阵 ,其 中, 矩阵 称为矩阵 与矩阵 的 , 记作 乘积 定义 即 2.矩阵乘法的定义
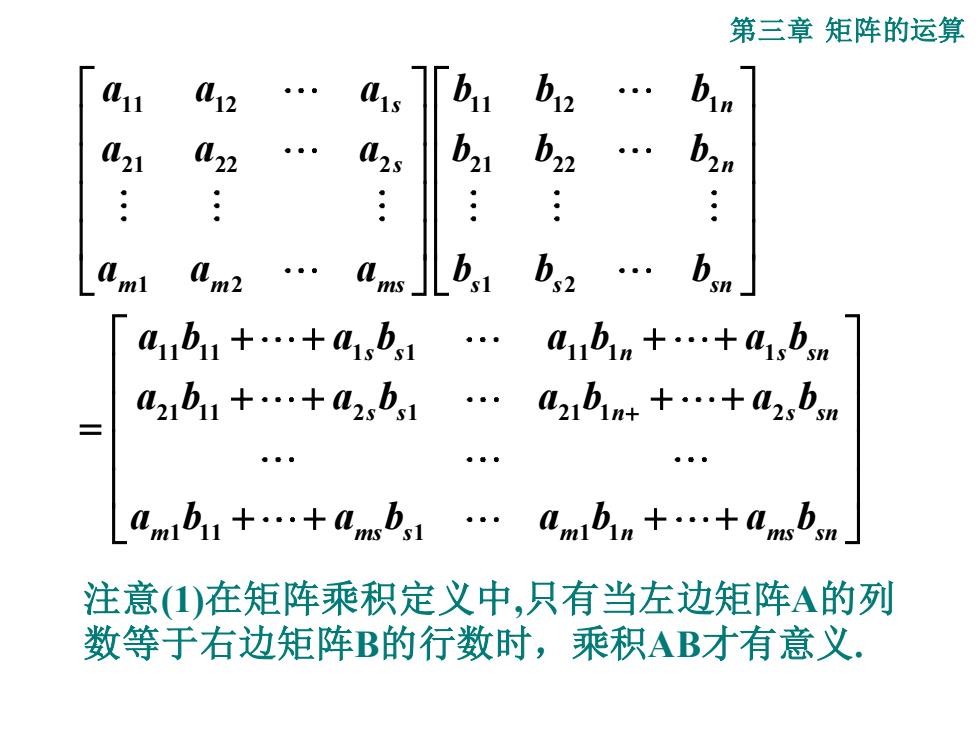
第三章矩阵的运算 L12 b11 b:2 021 41b1+.+4,b1 a1bn+.+a1,bm 21b1+.+2,b,1 .a2b1m++.+2,bm amb1+.+amb,1.ambin+.+ambm 注意(1)在矩阵乘积定义中,只有当左边矩阵A的列 数等于右边矩阵B的行数时,乘积AB才有意义
第三章 矩阵的运算 11 12 1 11 12 1 21 22 2 21 22 2 1 2 1 2 11 11 1 1 11 1 1 21 11 2 1 21 1 2 1 11 1 1 1 s n s n m m ms s s sn s s n s sn s s n s sn m ms s m n ms sn a a a b b b a a a b b b a a a b b b a b a b a b a b a b a b a b a b a b a b a b a b + + + + + + + + + = + + + + 注意(1)在矩阵乘积定义中,只有当左边矩阵A的列 数等于右边矩阵B的行数时,乘积AB才有意义