
例2.计算抛物线y2=2x与直线y=x-4所围图形 的面积. 解:由 y2=2x 得交点 y y=x-4 y+dy 8.4 (2,-2),(8,4) 为简便计算,选取y作积分变量, 0 y=x-4 则有 2,-2 .A=(y+4-3y2)dy =[3y2+4y-6y3]42=18
x 2 y x = 2 o y y x = − 4 例2. 计算抛物线 y 2x 2 = 与直线 的面积 . 解: 由 得交点 (2, − 2) , (8, 4) (8, 4) d A ( y 4 y )dy 2 2 1 = + − =18 y = x − 4 所围图形 (2, 2) − 为简便计算, 选取 y 作积分变量, 则有 y y + d y − = 4 2 A
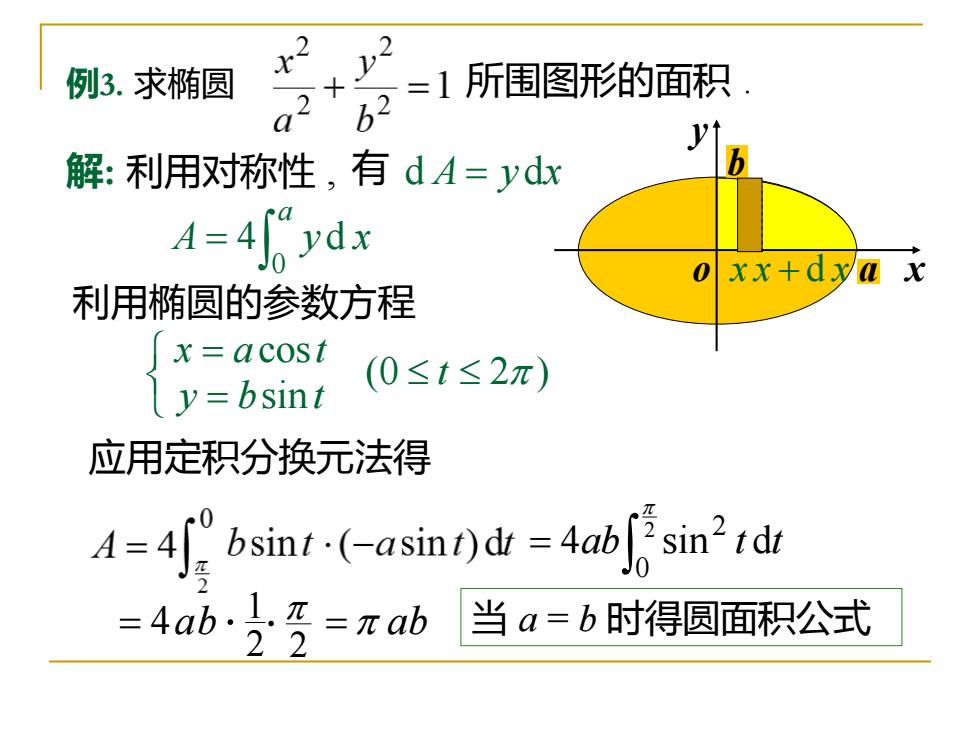
例3.求椭圆 =1所围图形的面积 62 少 解:利用对称性,有dA=ydx A=4l0ydx oxx+dya x 利用椭圆的参数方程 x=acost y=bsint (0≤t≤2π) 应用定积分换元法得 A=4f0bsin1-(←asint0)dt=4 absin2td =4a6:=ab 当a=b时得圆面积公式
a b o x y x 例3. 求椭圆 解: 利用对称性 , d A = y dx 所围图形的面积 . 有 = a A y x 0 4 d 利用椭圆的参数方程 (0 2 ) sin cos = = t y b t x a t 应用定积分换元法得 = 2 0 2 4 sin d ab t t = 4ab 2 1 2 = ab 当 a = b 时得圆面积公式 x + d x