
15.1.2关联,回路割集矩阵 ·关联矩阵 支路与结点的关系 ·回路矩阵 支路与回路的关系 割集矩阵 支路与割集的关系
15.1.2 关联,回路割集矩阵 • 关联矩阵 支路与结点的关系 • 回路矩阵 支路与回路的关系 • 割集矩阵 支路与割集的关系

图的矩阵表示 一.关联矩阵A 结点与支路的关系, 矩阵的行对应结点,列对应支路,矩阵中的元素值为-1,0,1 0表示对应的支路与结点没有直接连接 -1表示对应的支路与结点直接连接,支路电流的参考方向 是流入结点 1表示对应的支路与结点直接连接,支路电流的参考方向 是流出结点
1表示对应的支路与结点直接连接,支路电流的参考方向 是流出结点 图的矩阵表示 一.关联矩阵A •结点与支路的关系. 矩阵的行对应结点,列对应支路,矩阵中的元素值为-1,0,1 0表示对应的支路与结点没有直接连接 -1表示对应的支路与结点直接连接,支路电流的参考方向 是流入结点

图的矩阵表示 一.关联矩阵A 用矩阵形式描述节点和支路的关联性质 关联矩阵 A。={anxb 节点数 支路数 4%=1 有向支路j背离i节点 4-1 有向支路指向节点 4分=0 节点与j支路无关
图的矩阵表示 一.关联矩阵A 用矩阵形式描述节点和支路的关联性质 aij aij = 1 有向支路 j 背离 i 节点 aij= -1 有向支路j 指向 i 节点 aij =0 i节点与 j 支路无关 关联矩阵 Aa={aij}n b 节点数 支路数
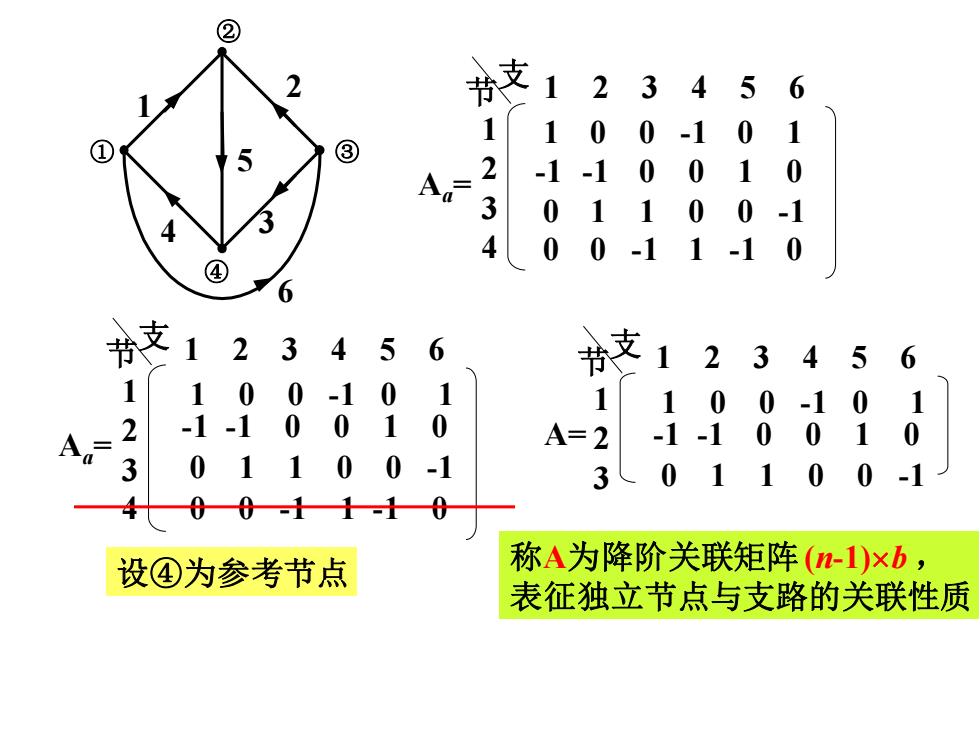
② 支 12 3 5 4 6 1 1 0 0 -1 01 ③ 2 -1-1 0 01 0 3 011 00-1 4 4 00-11-1 0 ④ 6 粉支 123456 节支1 2 3 4 5 6 1 1 0 0 -101 1 1 0 0 -1 0 1 An= 2 -1-1 010 A= 2 -1-1 0 0 1 0 3 01 .0 0-1 30 11 0 0-1 00-11-10 设④为参考节点 称A为降阶关联矩阵(-1)×b, 表征独立节点与支路的关联性质
6 4 5 3 2 1 ① ② ④ ③ Aa = 1 2 3 4 节 支 1 2 3 4 5 6 1 0 0 -1 0 1 -1 -1 0 0 1 0 0 1 1 0 0 -1 0 0 -1 1 -1 0 Aa = 1 2 3 4 节 支 1 2 3 4 5 6 1 -1 0 0 0 -1 1 0 0 0 1 -1 -1 0 0 1 0 1 0 -1 1 0 -1 0 设④为参考节点 A= -1 -1 0 0 1 0 1 2 3 节 支 1 2 3 4 5 6 1 0 0 -1 0 1 0 1 1 0 0 -1 称A为降阶关联矩阵(n-1)b , 表征独立节点与支路的关联性质
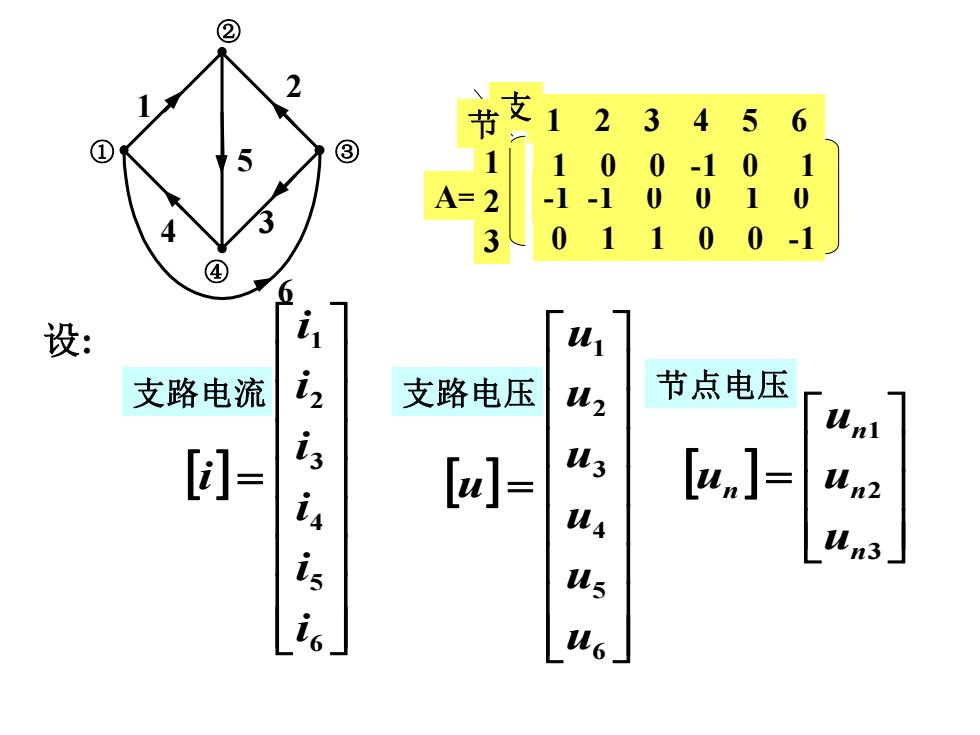
② 2 12 3 456 ① ③ 1 -101 2 -1-1 0 3 0 1 0 -1 设: 支路电流 支路电压 节点电压 42 [= [u]= [un]= Wn2 is Un3
设: 6 4 5 3 2 1 ① ② ④ ③ A= -1 -1 0 0 1 0 1 2 3 节 支 1 2 3 4 5 6 1 0 0 -1 0 1 0 1 1 0 0 -1 = 6 5 4 3 2 1 u u u u u u u 支路电压 = 6 5 4 3 2 1 i i i i i i i 支路电流 = 3 2 1 n n n n u u u u 节点电压