
信号与系锁电车派第一章信号与系统81-1绪论信号与系统一、信号传输系统1、消息和信号消息:语言、文字、图画、编码等信号:把消息转变成便于处理的光、电(随时间变化)2、通信系统的典型构成三、 信号与系统学科待发接收输入信号输出信号精鱼酸热量人及射机面过医收机胰换病消息、信号理论:信号分析:讨论信号的表示、信号的性质任务:传送消息信号处理:信号综合:例:电话:语言或音乐(消息)电流或电2、系统理论:压(信号)一接收端一电信号还原为声音系统分析:对于给定的系统,在输入信号作用下产生的输出信号81-2信号“信号"与“函数(或序列)”两个词互相通用系统综合:给定性能指标,设计一个满足性能指标的系统。一、信号的分类1、连续信号和离散信号3、与其它学科的关系连续信号:在连续时间范围内(-<t<)血烈究相性理治、混体聚(输型定义的信号f(t)=10sint论打下基础。例:1026
1 信号与系统电子课件 1、消息和信号 第一章 信号与系统 §1-1绪论 一、信号传输系统 消息:语言、文字、图画、编码等 2、通信系统的典型构成 信号:把消息转变成便于处理的 光、电(随时间变化) 任务:传送消息 转换器 转换器 发射机 信道 接收机 待发 消息 输入信号 输出信号 接收 消息 例:电话:语言或音乐(消息) 电流或电 压(信号) 接收端 电信号还原为声音 二、信号与系统学科 1、信号理论: 2、系统理论: 信号处理: 信号综合: 信号分析:讨论信号的表示、信号的性质 系统分析:对于给定的系统,在输入信 号作用下产生的输出信号 系统综合:给定性能指标,设计一个满 足性能指标的系统。 3、与其它学科的关系 为研究网络理论、通信理论、控制 理论、信号处理和信号系统检测理 论打下基础。 §1-2信号 “信号”与“函数(或序列)” 两个词互相通用。 一、信号的分类 1、连续信号和离散信号 连续信号:在连续时间范围内 定义的信号 (−∞ < t < ∞) 0 1 2 -10 10 t f (t) 10 sin t 1 = 例:
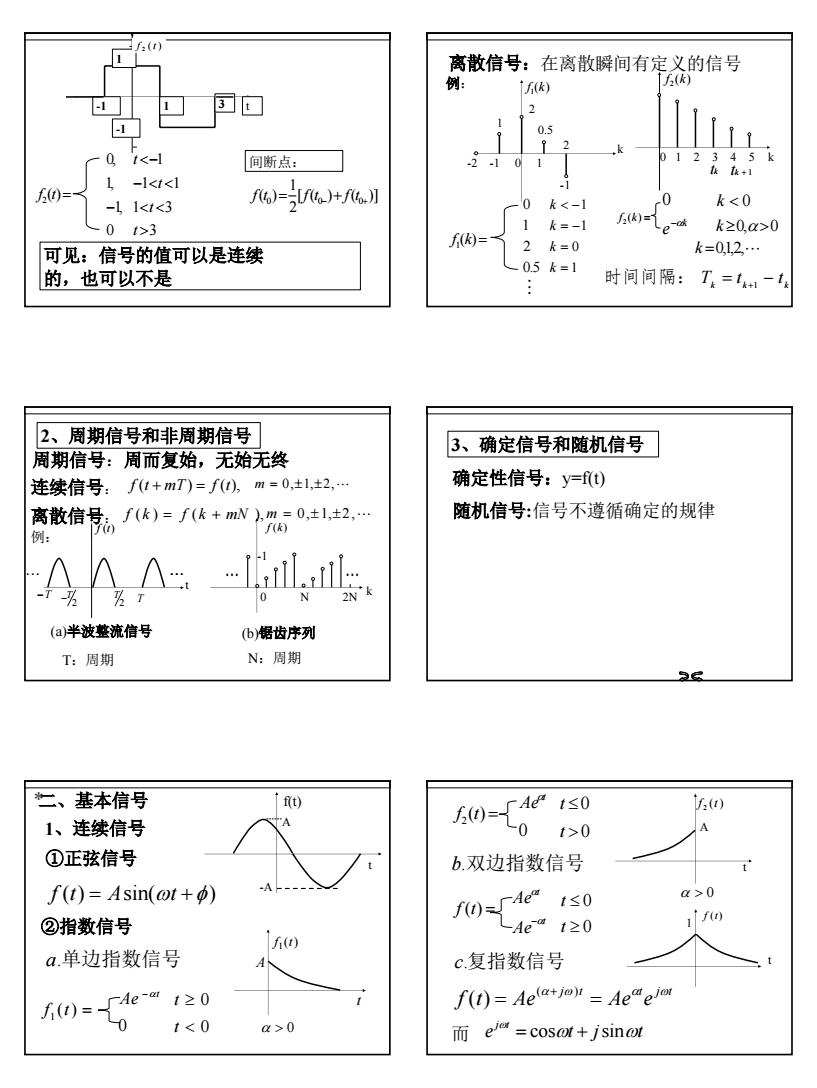
离散信号:在离散瞬间有定义的信号fe(k)例:[f(k)回口1酒0T<-1间断点:txt+1-l<t<1f(t)=F(6)-[(0)+(0.)]k<0-1 1<t<3Kk≥0,α>0k=-0f(k)=k=0k=0,12,.可见:信号的值可以是连续0.5k=1的,也可以不是时间间隔:T,=1-2、周期信号和非周期信号3、确定信号和随机信号周期信号:周而复始,无始无终确定性信号:y=f(t)F(t+mT)= f(0), m=0,±1,±2, 连续信号:随机信号:信号不遵循确定的规律离信,(k)=(+mN)=0,±1,±2,191(a)半波整流信号(b)锯齿序列N:周期T:周期*二、基本信号f(t)┌Aet≤0(0)f(0)=1、连续信号-0t>0①正弦信号b.双边指数信号AIf(t) = Asin(ot +g)α>0-Aeat≤0f(t)=f(t)②指数信号-Ae-at≥01f(0)a.单边指数信号c.复指数信号ANF(t)= Ae(a+j0) = Ae"ejar_Ae-α t≥0f.(t) =^L0t<0α>0而 eja" =cosat+jsinot
2 f2(t)= 0 1, 1, 0, − 3 1 3 1 1 1 > < < − < < <− t t t t [ ( ) ( )] 2 1 ( )0 = 0− + 0+ f t f t f t 间断点: 可见:信号的值可以是连续 的,也可以不是 -1 -1 1 1 3 t ( ) 2 f t f2 (k) = k e−α 0 k < 0 k ≥0,α>0 k =0,1,2," f 1(k)= 0.5 2 1 0 1 0 1 1 = = = − < − k k k k # 0 1 2 3 4 5 k ( ) 2f k tk tk + 1 -2 -1 0 1 k ( ) 1f k 2 1 0.5 -1 例: 2 离散信号:在离散瞬间有定义的信号 k k k T = t − t 时间间隔: +1 2、周期信号和非周期信号 连续信号: f (t + mT ) = f (t), m = 0,±1,±2," 周期信号:周而复始,无始无终 离散信号: f (k ) = f (k + mN ), m = 0,±1,±2," " " k f (k) 0 N 2N -1 (b)锯齿序列 N:周期 " " (a)半波整流信号 T:周期 t −T 2 −T 2 T T f (t) 例: " " 3、确定信号和随机信号 确定性信号:y=f(t) 随机信号:信号不遵循确定的规律 f (t) = Asin(ωt +φ) f1 (t) = 0 t Ae −α 0 0 < ≥ t t 1、连续信号 ①正弦信号 ②指数信号 a.单边指数信号 ∗二、基本信号 -A A t f(t) ( ) 1f t α > 0 t A f2(t) = 0 t Aeα 0 0 > ≤ t t f (t) = t t Ae Ae α α − 0 0 ≥ ≤ t t j t t j t f t Ae Ae e α ω α ω = = ( + ) ( ) b.双边指数信号 c.复指数信号 e t j t j t ω ω ω 而 = cos + sin f (t) t 1 A ( ) 2 f t t α > 0
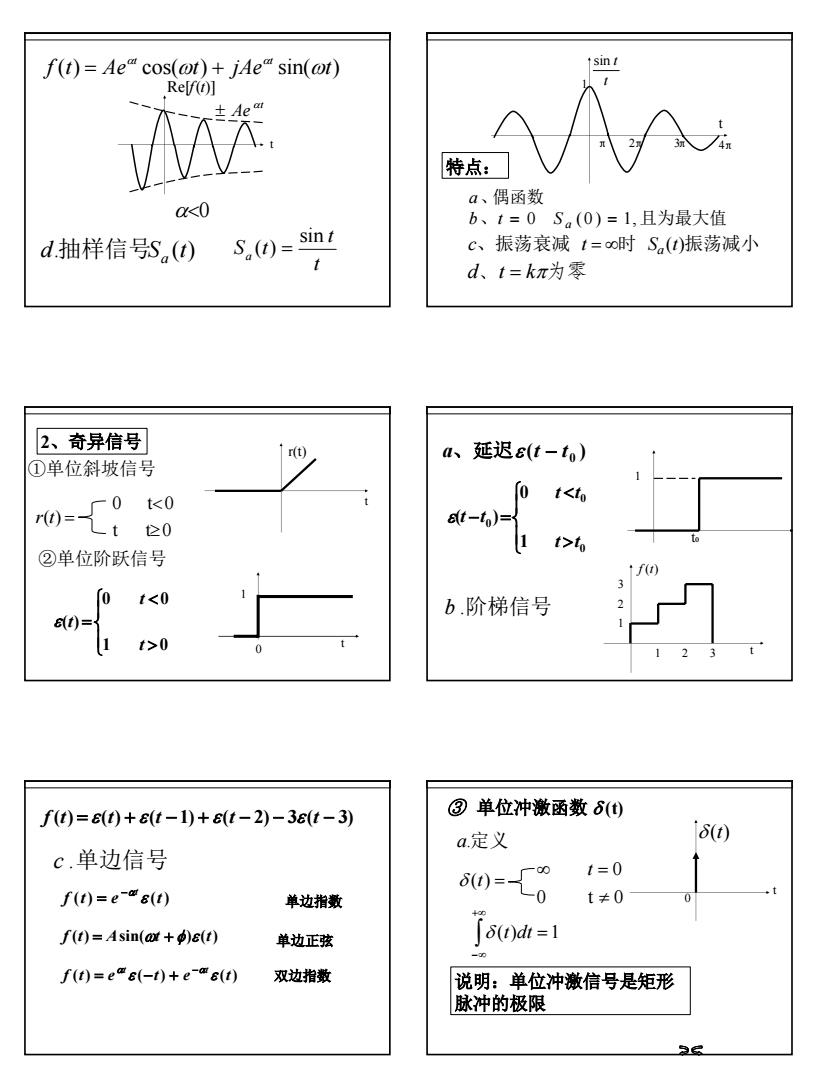
f(t)= Ae" cos(ot) + jAe" sin(ot)Ref(t)]A.一特点:a、偶函数K0b、t=0 S(0)=1,且为最大值sintC、振荡衰减 t=o0时 Sa(0)振荡减小d.抽样信号s.()S.(t) =d、t=k元为零2、奇异信号a、延迟e(t-t)rt①单位斜坡信号0t<to-00r0=°d(t-t)=}≥0t>t②单位阶跃信号f()ot<0b.阶梯信号8(t)=)t>0t③单位冲激函数 8(t)f(t)=e(t)+8(t -1)+ e(t - 2) - 3e(t - 3)s(t)a.定义c.单边信号t=08()=478-0I(t) =e-" 8(t)t+0单边指数[s(t)dt =1f(t)= Asin(at + p)e(t)单边正弦f(t)= ee(-t)+e-" s(t)双边指数说明:单位冲激信号是矩形脉冲的极限36
3 d. S (t) 抽样信号 a t t S t a sin ( ) = α<0 t Ae α ± Re[f(t)] t f (t) Ae cos( t) jAe sin( t) t t ω ω α α = + b、 t = 0 S a (0 ) = 1, 且为最大值 c、振荡衰减 t = ∞时 Sa (t)振荡减小 d、t = kπ为零 a、偶函数 特点: t sin t 1 π π3 4π t 2π t r(t) 2、奇异信号 r(t) = t t 0 0 t 0 ≥ < ①单位斜坡信号 ②单位阶跃信号 > < = 1 0 0 0 ( ) t t ε t 1 t 0 > < − = 0 0 0 1 0 ( ) t t t t ε t t t0 1 b .阶梯信号 t 1 2 3 1 2 3 f (t) ( ) 0 a、延迟ε t − t f (t) = ε(t) + ε(t − 1) + ε(t − 2) − 3ε(t − 3) c .单边信号 f (t) e (t) t ε −α = 单边指数 f (t) = Asin(ωt + φ)ε (t) 单边正弦 f (t) e ( t) e (t) t t ε ε α −α = − + 双边指数 δ (t) = 0 t 0 0 ≠ ∞ t = ( ) =1 ∫ +∞ −∞ δ t dt a.定义 δ (t) t 0 说明:单位冲激信号是矩形 脉冲的极限 ③ 单位冲激函数 δ (t)
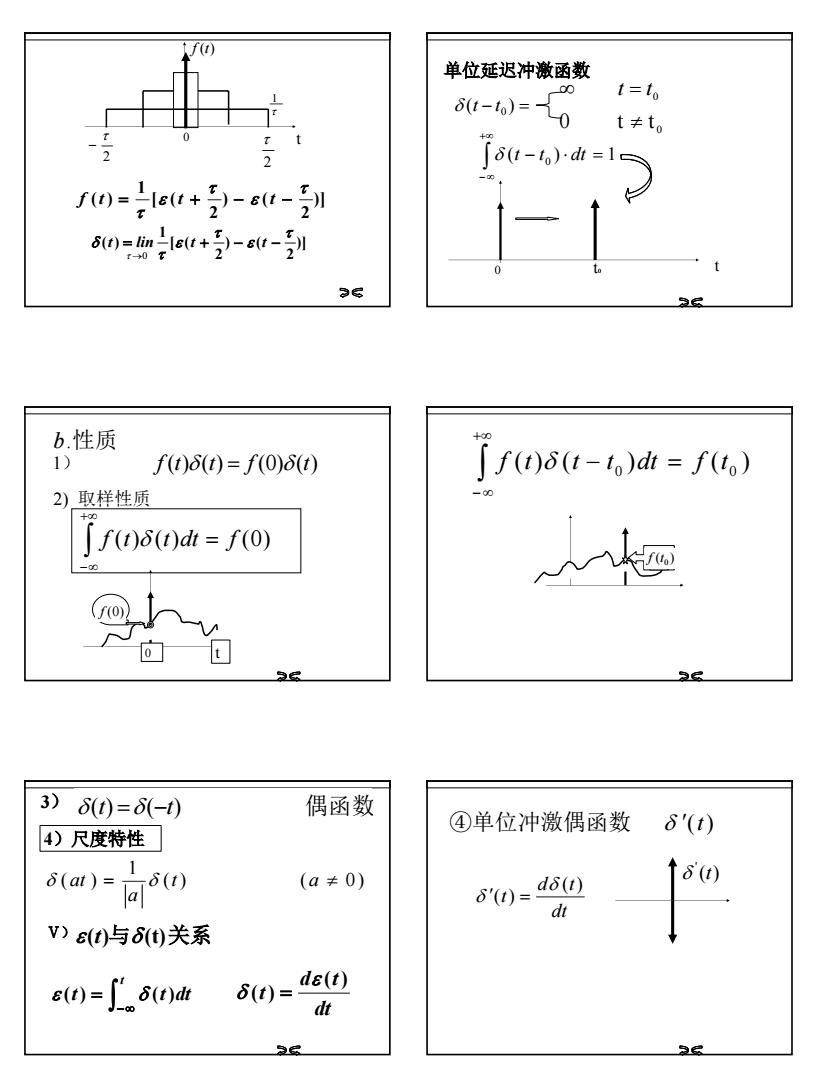
ft单位延迟冲激函数t=to8(t-to) =t+t.8(t-t)-dt =1.f (t)= -[e(t + ) - 8(t - )6(e(+-()36b.性质f(t)s(t- to)dt = f(to)1)f(t)8(t) = f(0)8(t)2)取样性质[ f(t)8(t)dt = f(0)Hf(o(roOF+3) (1)=(-1)偶函数④单位冲激偶函数'(t))尺度特性1(t)8(1)8(at)=(a + 0)de(t)8'(t) =dtV) e(t)与 (t)关系de(t)8(t)= f8(t)dt8(t) =dtd
4 )] 2 ) ( 2 [ ( 1 ( ) τ ε τ ε τ f t = t + − t − f (t) τ 1 2 τ 2 τ − 0 t )] 2 ) ( 2 [ ( 1 ( ) τ ε τ ε τ δ t = lin t + − t − τ →0 单位延迟冲激函数 0 t0 t δ (t − t0 ) = 0 0 0 t t ≠ ∞ t = t ( − 0 ) ⋅ = 1 ∫ +∞ −∞ δ t t dt 2) 取样性质 b.性质 f (t) (t)dt = f (0) ∫ +∞ −∞ δ 1) f (t)δ (t) = f (0)δ (t) t f (0) 0 ( )0 f t ( ) ( ) ( ) 0 0 f t t − t dt = f t ∫ +∞ −∞ δ 3) δ(t) =δ(−t) 偶函数 4)尺度特性 ( ) ( 0) 1 ( ) = t a ≠ a δ at δ Ⅴ)ε(t)与δ (t)关系 ∫−∞ = t ε (t) δ (t)dt dt d t t ( ) ( ) ε δ = dt d t t ( ) ( ) δ δ ′ = ④单位冲激偶函数 δ ′(t) ( ) ' δ t

特性( f(t)s(t-to)dt=-f(to)同取样性质+f(t)s'(t)dt()8"(0)dt =(-1)" f"(0)= f(t)8(1)- f'(0)s(t)dt =-f'(0)例:计算下列各题b.比较ts'(n)18(0)1ro(1)[ + sin()]8(t+2)dt00 (t +2F -2t+1)8(t-1)dt(2)e(0)= dr()8(1) = de()0(0)=d00)解:(原式[+sin()-=- 3in(e(0)-,8(0)dt80)= 8(0dr(t)-s(0)dt(2)原式= -[3t° +4t-2] = =-5③符号函数2.离散信号1>0定义sgn(t) =①单位样值序列-1 1<0Sgn(t)k=0-定义s(k)=L。1其它回sgn(t) = 8(t) - 8(-t)
5 ∫ +∞ −∞ f (t)δ ′(t)dt = f (t) (t) − f ′(t) (t)dt = − f ′(0) ∫ +∞ −∞ +∞ δ −∞ δ 特性 取样性质 ( ) ( ) ( 1) (0) n n n f t t dt = − f ∫ +∞ −∞ δ ( ) ( ) ( ) 0 0 f t ′ t −t dt = − f ′ t ∫ +∞ −∞ 同 δ 理 t r(t) t δ ′(t) t δ (t) ⑴ dt dr t t ( ) ε ( ) = dt d t t ( ) ( ) δ δ ′ = dt d t t ( ) ( ) ε δ = b .比较 t 1 ∫−∞ = t r(t) ε (t)dt ∫−∞ = t ε (t) δ (t)dt ∫−∞ = ′ t δ (t) δ (t)dt t dt t t )] ( 2) 4 [ sin( 2 + + − ∞ ∞ ∫ δ π 例:计算下列各题 (1) (2) (t 2t 2t 1) (t 1)dt 3 2 + − + ′ − −∞ ∞ ∫ δ 解:(1)原式= )] 3 4 [ sin( 2 2 + t = − = t t π (2)原式= [3 4 2] 5 1 2 − t + t − t= = − ⑤符号函数 sgn( t) = 1 0 1 0 − < > t t 定义 sgn(t) = ε(t) − ε(−t) t +1 -1 Sgn(t) δ (k) = 0 1 k = 0 定义 其它 ① 单位样值序列 -3 -2 -1 1 2 3 1 2. 离散信号