《电路》课程教学资源（PPT课件）第10章 含有耦合电感的电路

第十章含有耦合电感的电路 9.1互感 9.2有互感的电路的计算 9.3空心变压器 9.4全耦合变压器和理想变压器

第十章 含有耦合电感的电路 9. 1 互感 9. 3空心变压器 9. 2 有互感的电路的计算 9. 4 全耦合变压器和理想变压器 `

9.1互感和互感电压 一、互感和互感电压 N .21 当线圈1中通入电流，时，在线圈1中产生磁通(nagnetic flux), 同时，有部分磁通穿过临近线圈2。当为时变电流时，磁通也将 随时间变化，从而在线圈两端产生感应电压。 更1=Φ21+更1 i1,N1→平=N1D1L1=i1 总磁通想醛》 漏磁通 中21在线圈N2产生磁链！ 平1=N2④21 定义：M1= 21 为线圈1对2的互感系数，单位亨（田 (mutual inductance coefficient) 当i1、41、山21方向与Φ符合右手定则时，根据电磁感应定律： d4= d 21= dΨ21=M21 di 41:自感电压； dt dt dt dt 山21：互感电压

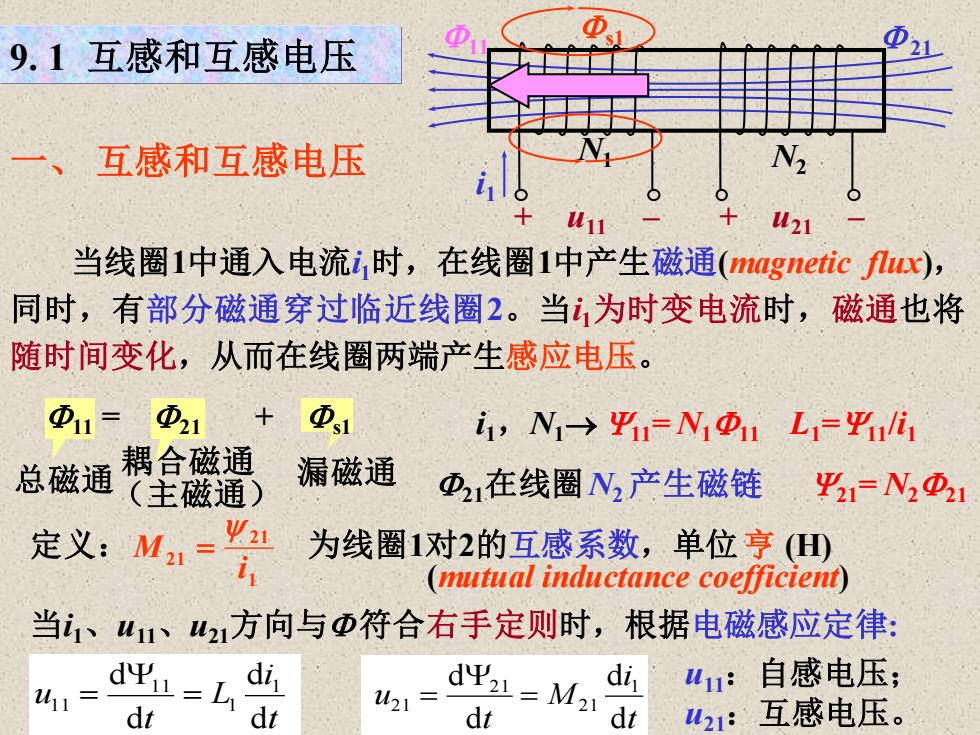
9. 1 互感和互感电压 一、 互感和互感电压 + u11 – + u21 –  21 i1 N1 N2 当线圈1中通入电流i1时，在线圈1中产生磁通(magnetic flux)， 同时，有部分磁通穿过临近线圈2。当i1为时变电流时，磁通也将 随时间变化，从而在线圈两端产生感应电压。 s1 i1，N1→ Y11= N111 L1=Y11/i1 总磁通 21在线圈N2 产生磁链 Y21= N221 耦合磁通 漏磁通 （主磁通） 11 = 21 + s1 定义： 为线圈1对2的互感系数，单位亨 (H) 1 21 21 i M  = (mutual inductance coefficient) 11 当i1、u11、u21方向与 符合右手定则时，根据电磁感应定律: d d d d 1 1 11 11 t i L t u = Y = t i M t u d d d d 1 21 21 21 = Y = u11：自感电压； u21：互感电压

同理，当线圈2中通电流时会产生磁通④2，④12。，为时变时 线圈2和线圈1两端分别产生感应电压422,412· W12 W22 L2=Y2/i2 2,N2→2 /①2 Y12 M2=2 为线圈2对1的互感 可以证明：M12=M21=M。 当1、411、21方向与Φ符合右手定则时，根据电磁感应定律： dM dt z 22= dΨ22=9 dt dt dt =L dt dt

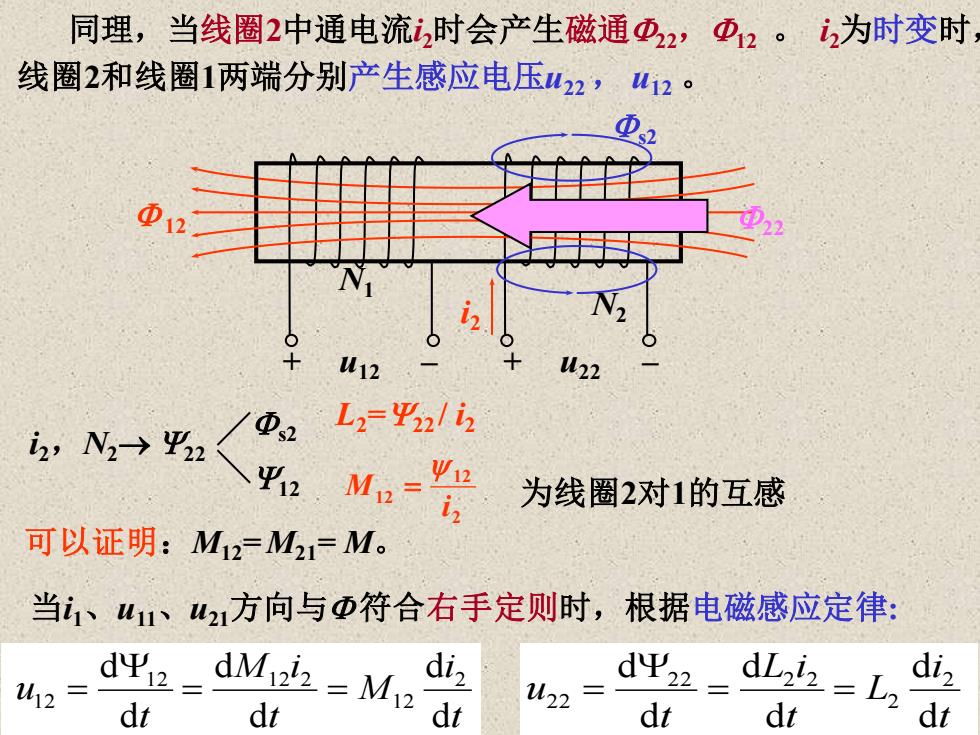
可以证明：M12= M21= M。 同理，当线圈2中通电流i2时会产生磁通22，12 。 i2为时变时， 线圈2和线圈1两端分别产生感应电压u22 ， u12 。 d d d d d d 2 2 2 2 2 2 2 2 t i L t L i t u = = Y = t i M t M i t u d d d d d d 2 1 2 1 2 1 2 2 1 2 = = Y = 2 12 12 i M  = 为线圈2对1的互感 i2，N2→ Y22 s2 Y12 L2=Y22 / i2 + u12 – + u22 – i2  12 N1 N2 s2 22 当i1、u11、u21方向与 符合右手定则时，根据电磁感应定律:

当两个线圈同时通以电流时， ①1 每个线圈两端的电压均包含 自感电压和互感电压： 11 W21 ∫=4+“：=4 M. dt iz 题=业+EM验+凸G 在正弦交流电路中，其相量形式的方程为 「U1=jwL,i1+jwM2i2 U2=joMaI1+j@L2I2

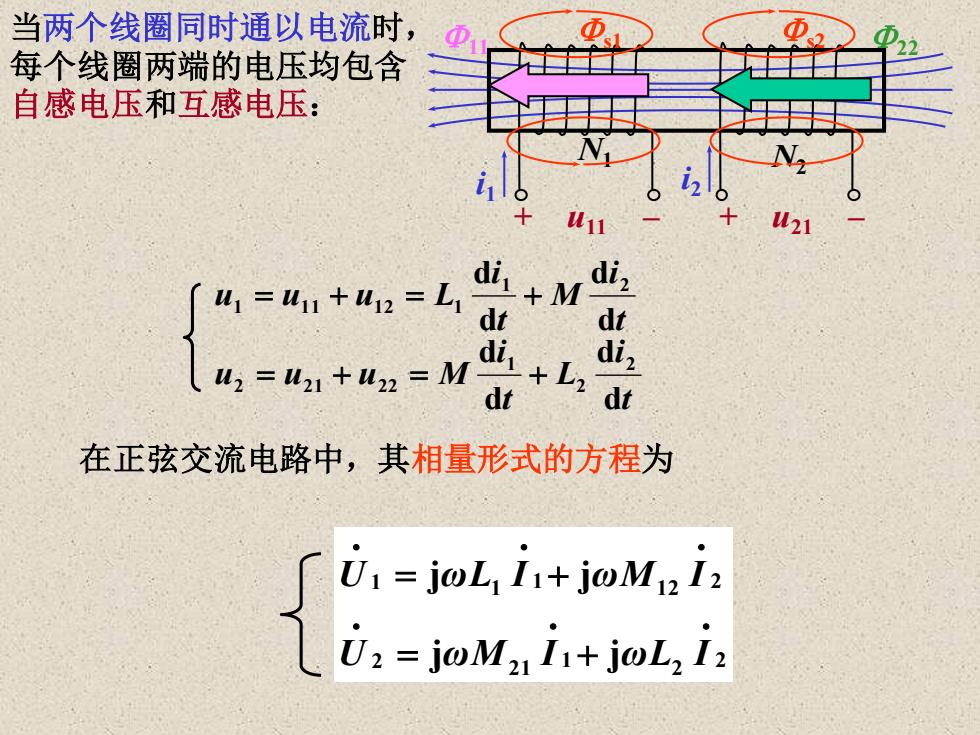
当两个线圈同时通以电流时， 每个线圈两端的电压均包含 自感电压和互感电压： t i L t i u u u M t i M t i u u u L d d d d d d d d 2 2 1 2 2 1 2 2 1 2 1 1 1 1 2 1 = + = + = + = + 在正弦交流电路中，其相量形式的方程为 2 2 1 21 2 2 12 1 1 1 j j j j • • • • • • = + = + U ωM I ωL I U ωL I ωM I + u11 – + u21 – i1 N1 N2  s1 11 s2 i2 22

1.互感的性质 ①从能量角度可以证明，对于线性电感M12=M1=M ②互感系数M只与两个线圈的几何尺寸、匝数、相互位置 和周围的介质磁导率有关，如其他条件不变时，有 Mo N N2 (Lo N2) 2.耦合系数(coupling coefficient)k: k表示两个线圈磁耦合的紧密程度。 M 可以证明，≤1。 VLL2 全耦合：D、1=①20 即④11=④21，④22=④12 :h=N9,h-N,0,M1-N,M。-V@ i .Mi2M2=LL2 M2=LL .k=1

2.耦合系数 (coupling coefficient) k： k 表示两个线圈磁耦合的紧密程度。 全耦合:  s1 =s2=0 1 2 def L L k = M 即 11= 21 ， 22 =12 , 1 , , , 1 2 2 1 2 2 1 1 2 2 1 1 2 1 2 1 2 2 1 2 1 2 2 2 2 2 1 1 1 1 1  = =  = = = = = M M L L M L L k i N Φ M i N Φ M i N Φ L i N Φ  L 可以证明，k1。 1. 互感的性质 ①从能量角度可以证明，对于线性电感 M12=M21=M ②互感系数M 只与两个线圈的几何尺寸、匝数 、 相互位置 和周围的介质磁导率有关，如其他条件不变时，有 M  N1N2 （L  N2）