第五章连续系统的S域分析S5-1拉普拉斯变换由付氏变换引入拉氏变换作用①可以将微分方程化为代数方程f(t)(如u(t),不满足绝对②自动将初始条件包含在变换中,可求解全响应③某些付氏变换不存在的信号拉氏变换存在0(0).e-a可积, (u(0)ldt →)可以用S域观点来分析系统二。拉普拉斯反变换α>0绝对可积今=f()e-aI ro+m F(s)e" dss=o+jof(t)=(jo)= f f(t)e-"e-an dt2元gJa-j(jo)= F(s)= f(t)e" dtF(s) =LT-'[f(0)]记为双边拉普拉斯变换三。 拉普拉斯变换的收敛域F(s)= J f(1)e-" diF(s) - (te" dt单边拉普拉斯变F(s)= LT [f(O))记为1、双边拉普拉斯变换收敛域:使F(S)存在的s的区域称为收敛域。(1).因果信号实际上就是拉氏变换存在的条件;f()是因果函数例:设f(t)=e"u(t)lim f(t)e =0(a>a.)e(a-s)oF(s)-e"e-s'di a-s当a-<0, 即>a时,F(s)收敛au(t)
1 第五章 连续系统的S域分析 ①可以将微分方程化为代数方程 ④可以用S域观点来分析系统 ③某些付氏变换不存在的信号拉氏变换存在 ②自动将初始条件包含在变换中,可求解全响应 作用 §5-1 拉普拉斯变换 一.由付氏变换引入拉氏变换 , ( ( ) ) ( )( ( ) , → ∞ ∫ +∞ −∞ u t dt f t u t 可积 如 ) 不满足绝对 t t u t e −σ ( ) ⋅ 令φ(t) = f (t)e −σt α > 0 绝对可积 ( j ) f (t)e e dt σt jωt ω − − +∞ ∫−∞ Φ = ( j ) F(s) f (t)e dt −st +∞ ∫−∞ Φ ω = = 记为 F (s) = LT [ f (t)] ( ) ( ) 0 F s f t e dt −st +∞ ∫ − = s =σ + jω 双边拉普拉斯变换 单边拉普拉斯变换 二.拉普拉斯反变换 F s e ds j f t st j j ( ) 2 1 ( ) ∫ + ∞ − ∞ = σ π σ ( ) LT [ ( )] 1 F s f t − 记为 = 三.拉普拉斯变换的收敛域 F(s) f (t)e dt −st +∞ ∫−∞ = ( ) 0 lim f (t) e 0 σ σ σ t t = > − →∞ 收敛域:使F(s)存在的s的区域称为收敛域。 实际上就是拉氏变换存在的条件; O σ jω σ0 收敛坐标 收敛轴 收敛区 : f (t) e u(t) at 例 设 = F s e e dt at −st ∞ ∫ − = 0 ( ) − ∞ − = 0 1 (a s)t e a s 当a −σ < 0, 即 σ > a时, F(s)收敛 1 t e u(t) at a < 0 a < 0 jω a 0 σ (1).因果信号 f (t)是因果函数 1、双边拉普拉斯变换
无界o>ae-(s-a) 0u(t-(s-a)lg<a-(s-a)a>0a>0收敛域ja(2)反因果函数的收敏域f(t)= ea" u(-t)aoF(s)= ['ee-"dta>0a>0(3-双边函数的收敛域aj>a2aft<o<a设有()=()+()=lea t>0adnF(s)= [° f(t)e-" dtaF(s)的收敛域不存在F(s)的收敛域F(s)不收敛=" (0)u(-1)e"d + ()u(0e-"dt2.单边拉普拉斯变换专过因果信号= F(s)+ F2(s)双边拉普拉斯变换同单边拉普拉期常用信号的拉氏变换(3).指数函数(1),单位阶跃函数u(t)f(t)=e"u(t)-e-(s+a)|0~F(s)=J,u(ve-"dt-J"-"dt=-e-sl°F(o)-Ied--+ae/R[s]>0R,[s]>-a"s+a【2)单位冲激函数8((4)复指数函数f(t) = e*jlu(t)F(s)-J8(ne"dt=e- =1F(s)= I eme"d = -s± joR.[s]>0收敛域为全平面
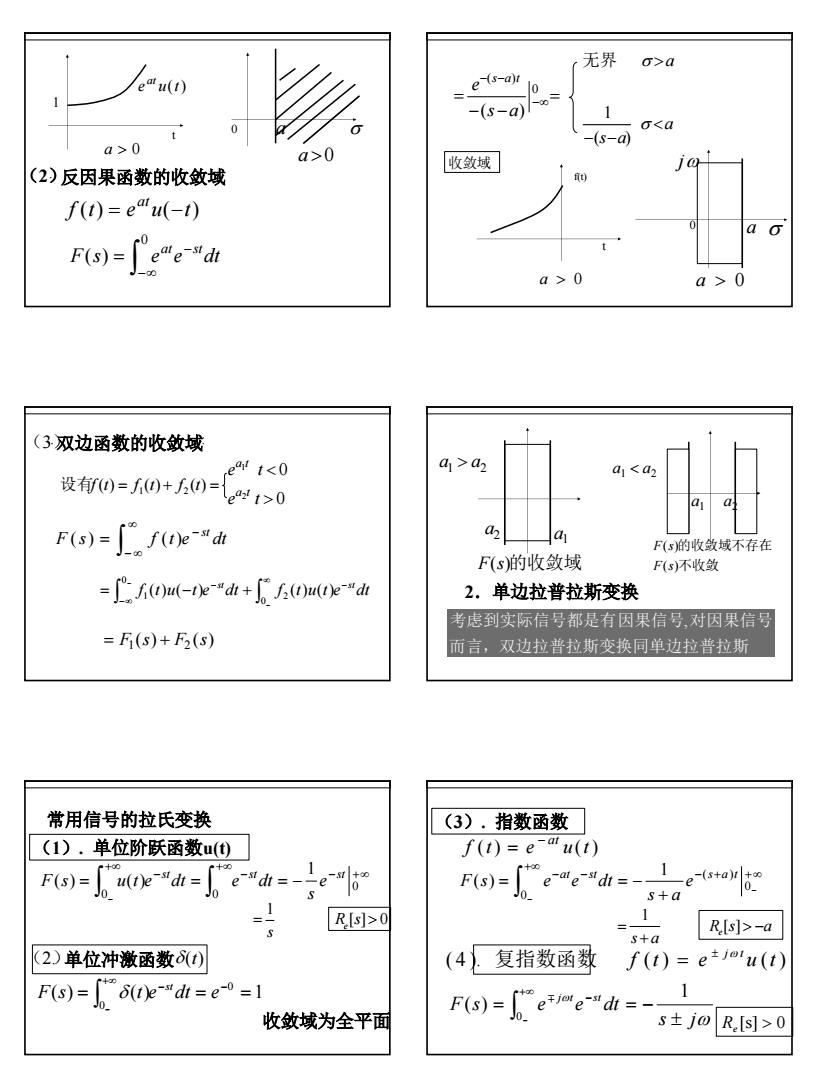
2 1 t e u(t) at a > 0 a >0 0 a σ (2). 反因果函数的收敛域 f (t) e u( t) at = − F s e e dt at −st −∞ ∫ = 0 ( ) = − − = −∞ − − 0 ( ) (s a) e s a t a s a a < − − > σ σ ( ) 1 无界 收敛域 t a > 0 f(t) jω a > 0 0 a σ F s f t e dt − st ∞ − ∞ ∫ ( ) = ( ) f t u t e dt f t u t e dt st −st ∞ − ∫−∞ ∫ − − = − + 0 2 0 1 ( ) ( ) ( ) ( ) 设有f (t) = f1(t) + f2 (t) = 0 0 2 1 > < e t e t a t a t (3. )双边函数的收敛域: ( ) ( ) 1 2 = F s + F s a2 a1 a1 > a2 F(s)的收敛域 a1 < a2 a1 a2 不收敛 的收敛域不存在 ( ) ( ) F s F s 2.单边拉普拉斯变换 考虑到实际信号都是有因果信号 对因果信号 , 而言,双边拉普拉斯变换同单边拉普拉斯 (2.)单位冲激函数δ(t) [ ] 0 1 = R s > s e (1). 单位阶跃函数u(t) 常用信号的拉氏变换 − − +∞ +∞ − +∞ = = = − ∫ ∫ − 0 0 0 1 ( ) ( ) st st st e s F s u t e dt e dt ( ) ( ) 1 0 0 = = = − − +∞ ∫ − F s t e dt e st δ 收敛域为全平面 f (t) e u (t) − at = (3). 指数函数 − − + +∞ +∞ − − − + = = − ∫ 0 ( ) 0 1 ( ) at st s a t e s a F s e e dt R s a s a e > − + = [ ] 1 ( 4 ). f (t ) e u (t ) ± jω t 复指数函数 = [s] > 0 Re 1 ( ) 0 ω ω s j F s e e dt j t st ± = = − − +∞ ∫ − ∓

35-2拉普拉斯变换的性质一。 线性性质(5). cosotu(t), sinotu(t)f(t)αF(s)f()αF(s)cosol-)(e+-m)()f(t)= f(t)+ βf () α F(s) = aF(s)+ βF;(soo- R>0微分积分性质1微分性质设F(s)= L[(t)(ejor -e-jor )u()e-" dtL[sinoti(0)= J%)=SF()- (0-/函数的初始值d')=s°F(s)-s(0_)-J(0))=+0R[]>02- jo+$+jo(1=$"F()-s(0)-s(0.)F(s)f。 f(t)dt}=推广-sr(a-2)(0_)- (-1(0_)S降幂排列S"S"-… s’ soA"F(s)f(t)dt)=-升导数F(0), f-(0) , f"(0)三、平移性质2.原函数积分1.时域平移 ()dtl=↓F(o)+-(0.)若LLf(t)u(t)= F(s)其中(-)(o)=[(x)dx则 L[f(t-to)u(t- to)] =e-o F(s)2.频域平移四.尺度变化特性若 F(s)=L[f(t))L[(an)]-_F(-)频域位移五。初值定理和终值定理则 L'[F(s-so)]=e f(t)利用频移特性①初值定理(0+)=lin f(0)=linsF(s)Lle-a sinop]=-(s+a)° +o)定理成立条件:linsF(s)存在st②终值定理Lea cosobl= (s+a) +abf(o0)=lig SF(s)
3 (5). cosωtu(t), sinωtu(t) ( ) ( ) 2 1 cos t u(t) e e u t jωt jωt ω − ⋅ = + 2 2 ) 1 1 ( 2 1 L[cos ( )] ω ω ω ω + = + + − = s s s j s j tu t e e u t e dt j tu t j t − j t −st +∞ = − ∫ ( ) ( ) 2 1 L[sin ( )] 0 ω ω ω 2 2 ) 1 1 ( 2 1 ω ω ω ω + = + + − = j s j s j s [s] > 0 Re Re[s] > 0 ( ) ( ) ( ) ( ) 1 1 2 2 f t ↔F s f t ↔F s §5-2 拉普拉斯变换的性质 二. 微分积分性质 一.线性性质 ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 f t = αf t + βf t ↔ F s = αF s + βF s 设F(s) = L [ f (t)] [ ] ( ) (0 ) (0 ) 2 2 2 − − = s F s −sf − f ′ dt d f L [ ] ( ) (0 ) = − − sF s f dt df L 1 微分性质 函数的初始值 S降幂排列 升导数 2.原函数积分 (0 ) (0 ) [ ] ( ) (0 ) (0 ) ( 1) 1 ( 2) 1 2 − − − − − − − − − = − − ′ n n n n n n n sf f s F s s f s f dt d f L " (0 ) 1 ( ) 1 [ ( ) ] ( 1) − − −∞ = + ∫ f s F s s L f d t τ τ 1 1 0 S S s s n n− " (0 ), , (0 ) , (0 ) - 1 - 0 −2 − − n n f " f f ∫ − −∞ − − = 0 ( 1) 其中 f (0 ) f (x)dx ( ) 1 [ ( ) ] 0 F s s L f d t = ∫ − τ τ ( ) 1 [ ( ) ] 0 F s s L f d n n t = ∫ − τ τ 推广: 三. 平移性质 1. 时域平移 若L[ f (t)u(t)] = F(s) L[ ( ) ( )] ( ) 0 0 0 f t t u t t e F s −st 则 − − = 2. 频域平移 若 F (s) = L[ f (t)] 则 L-1[F(s − s0 )]= es0t f (t) 频域位移 利用频移特性 2 0 2 0 0 ( ) L[ sin ] α ω ω ω α + + = − s e t t 2 0 2 0 ( ) L[ cos ] α ω α ω α + + + = − s s e t t 四. 尺度变化特性 ( ) 1 L[ ( )] a s F a f at = 五. 初值定理和终值定理 ①初值定理 f (0 ) = lin f (t) = lin sF(s) + → + t 0 s → ∞ 定理成立条件 : s lin → ∞ sF (s) 存在 ②终值定理 f (∞) = lin sF(s) s→0

六。卷积定理定理成立条件:linf(t)存在f()F(s)f(t)αF(s)应用:a已知F(S)只要知道f(Q)和(0)b. 可检验 F(s)是否正确LL()*f2(0)=F(s)F2(s)二F(s)*F(s)(-2(0)元绿茶例:利用常用函数的的象函数及拉普拉斯② cos(βt)≤-?+β2变换的性质,求下列函数的拉普拉斯变换s+ae- cos(βt) -(s+α)+β2①e'[e(t)-s(t-2)]s+α- te-a cos(βt) 一 (=e'e(t)-ee-(-2)e(t-2)(s+α) +β2e-2 e~21-e-2(s+1)β? -(s+α)2F(s) =s+1s+1[(s+α)’+ β"]?$+1e-"(21-1)F(3)e-②已知f(1)的象函数F(s)=5?-S+1求e-3 f(2t-1)的象函数。"f(t)- F(s)2204J(21) -FG)3? +4s+7(2r-1)= 12(-1FGe
4 : . ( ), (0 )+ 应用 a已知F s 只要知道 f 和 b. 可检验 F (s)是否正确 f (∞) 定理成立条件: t lin → ∞ f (t)存在 , (0 ) ? 1 : ( ) = f + = s 例:已知 F s 求 (0 ) lim ( ) lim ( ) 1 0 = = = → →∞ + + f f t sF s t s ( ) ( ) ( ) ( ) 1 1 2 2 f t ↔F s f t ↔F s 六. 卷积定理 ( ) ( ) 2 1 L[ ( ) ( )] 1 2 1 2 f t ⋅ f t = F s ∗F s π L[ ( ) ( )] ( ) ( ) 1 2 1 2 f t ∗ f t = F s F s 例: 利用常用函数的的象函数及拉普拉斯 变换的性质,求下列函数的拉普拉斯变换。 ① [ ( )− ( −2)] − e t t t ε ε ( ) ( 2) 2 ( 2) = − − − − − − e t e e t t t ε ε 1 1 1 ( ) 2 2 + − ⋅ + = − − s e e s F s s 1 1 2( 1) + − = − + s e s ② 2 2 cos( ) β β + ⇔ s s t 2 2 ( ) cos( ) α β α β α + + + − ⇔ s s e t t ) ( ) cos( ) ( 2 2 ′ + + + − − ⇔ α β α β α s s te t t 2 2 2 2 2 [( ) ] ( ) α β β α + + − + = s s f (t) ⇔ F(s) ∴ ) 2 ( 2 1 (2 ) s f t ⇔ F ② 求 的象函数。 已知 的象函数 , (2 1) 1 1 ( ) ( ) 3 2 − − + = − e f t s S f t F s t 2 ) 2 ( 2 1 )] 2 1 (2 1) [2( s e s f t f t F − − = − ⇔ 2 3 3 ) 2 3 ( 2 1 (2 1) + − − + − ⇔ s t e s e f t F 2 3 2 1 2 3 ) 2 3 ( 1 2 1 + − + + − + = × s e s s 4 7 2 2 2 3 + + = + − s s e s
当m<n,F(s)为有理真分式S5-3拉普拉斯逆变换分解I ro+P F(s)e"ds(0)=2%)0-m一.查表法:从变换表或数学手册直接查得.极点和零点二、部分分式法零点通常F()具有如下的有理分式形式:A4(s)_ ms"+a.-s"+.a,s+aoF(0)--++h极点a,b,为实数, m,n为正整数。2.F(s)的极点为单实根k =(s - S)F(s) s=siA(s)同理 k, =(s - s,)F(s)s=siF()=b.(s-s)(s-s2)(s-s,)故: f(t)=(ke'*+ke +.+k,e")u(t)由代数理论k+k++k.s-stts-s2S-Sn2s +=0.6k -(s+5)F(s)-- 2s+1" s(s + 2)例1. 求F(s)=一的逆变换s(s + 2)(s + 5)0-{+05e*-0.- )(解:极点: S,=0,s2=-2,53=-53.极点含共轭复数根F(s)=+k,+$+2+$+5AQF()=D(ols+a) +β?s+k = F(0) (+2($+5)0 101.142s+1=Ts+a-jp+a+i (+2)()-+)-0
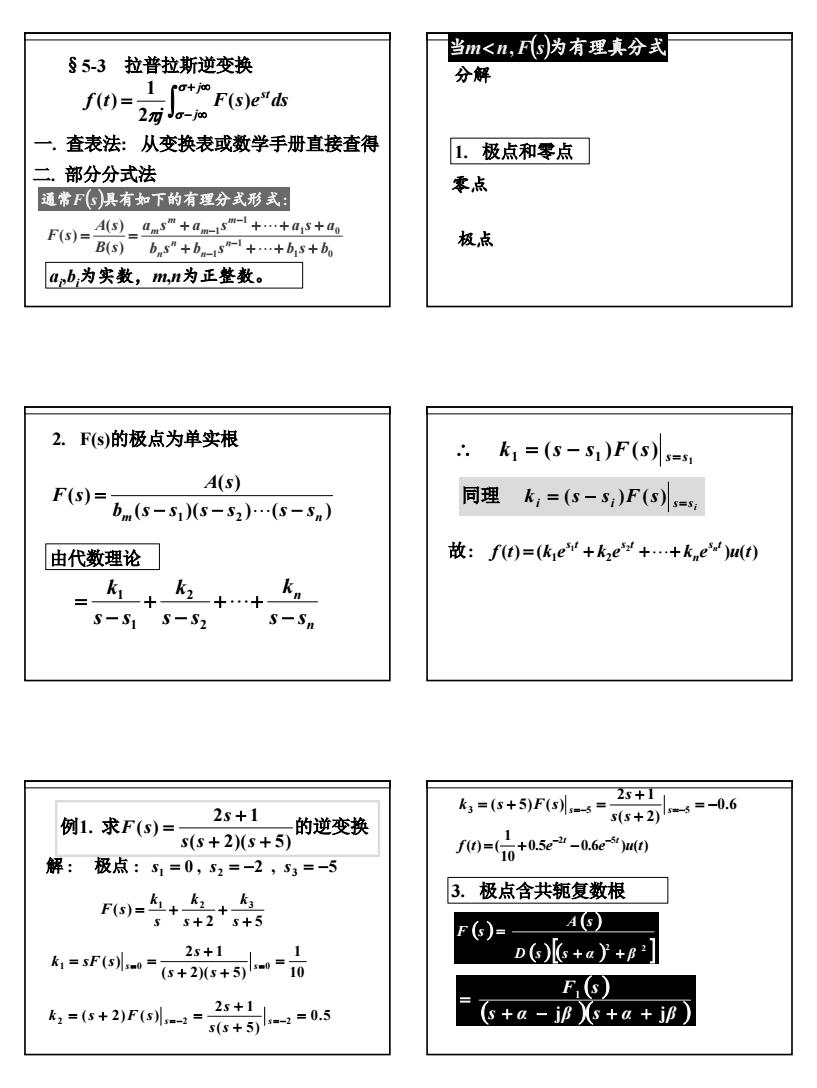
5 §5-3 拉普拉斯逆变换 F s e ds j f t st j j ( ) 2 1 ( ) ∫ + ∞ − ∞ = σ π σ 一. 查表法: 从变换表或数学手册直接查得 二. 部分分式法 1 0 1 1 1 0 1 1 ( ) ( ) ( ) b s b s b s b a s a s a s a B s A s F s n n n n m m m m + + + + + + + + = = − − − − " " ai ,bi 为实数,m,n为正整数。 通常F( )s 具有如下的有理分式形式: ( )( ) ( ) ( )( ) ( ) ( ) ( ) ( ) 1 2 1 2 n n m m b s p s p s p a s z s z s z B s A s F s − − − − − − = = " " 分解 零点 极点 z1 ,z2 ,z3"zm是A(s) () = 0的根,称为F s 的零点 p1 , p2 , p3"pn是B(s) () = 0的根,称为F s 的极点 当m< n,F(s)为有理真分式 1. 极点和零点 2. F(s)的极点为单实根 ( )( ) ( ) ( ) ( ) m 1 2 n b s s s s s s A s F s − − − = " 由代数理论 n n s s k s s k s s k − + + − + − = " 2 2 1 1 : ( ) ( ) ( ) 1 2 1 2 f t k e k e k e u t s t n s t s t n 故 = + +"+ 1 ( ) ( ) 1 1 s s k s s F s ∴ = − = i i i s s k s s F s = − = 同理 ( ) ( ) 例 求 的逆变换 ( 2)( 5) 2 1 1. ( ) + + + = s s s s F s : : 0 , 2 , 5 解 极点 s1 = s2 = − s3 = − 2 5 ( ) 1 2 3 + + + = + s k s k s k F s 10 1 ( 2)( 5) 2 1 ( ) 1 0 0 = + + + = s= = s= s s s k sF s 0.5 ( 5) 2 1 ( 2) ( ) 2 2 2 = + + = + s = − = s = − s s s k s F s 0.5 0.6 ) ( ) 10 1 ( ) ( 2 5 f t e e u t − t − t = + − 0.6 ( 2) 2 1 ( 5) ( ) 3 5 5 = − + + = + s=− = s=− s s s k s F s 3. 极点含共轭复数根 ( ) ( ) ( )( ) [ ] 2 2 D s s α β A s F s + + = ( ) ( )( ) s α β s α β F s j j 1 + − + + =