《信号与系统》课程授课教案（课件讲稿）第4章 连续系统的频域分析

第四章连续系统的频域分析Ci2 = 84-1信号分解为正交函数V.正交函数和正交函数集KB当，，完全重合，则=0,c2=11.正交矢量V.Ci2 V.随着夹角 8 增大，C12 威小;cos 0VV.当0=90,Ci2=0，和相互垂直C12=|cos 0 商网a.平面，x、y正交坐标系c. 般:Vy-0, itj令x方向正交单位失量LV=k矢量：令，y方向正交单位矢量A-C+Cy+.+CY.A=CV,+Cy,C.为A在V.中的投影b.三维，x、y、z正交坐标系C,=A正交量集,,)A=CV,+CV, +CV.3.正交函数集2. 正交函数①正交函数集定义：在(1,)区间内，若函数()和p,(1)定义：若n个函数(),,(1)，,(0)满足构成一个函数集,且在区间（t,t)内满足T"0.(0)g:(0)t = 0r0ij"o(t)0;(t)dt =3Lk,0 i=j则称 g,(t)和 pz()在区间 (ti,t,)内正交称此函数集是(t1,t2)区间上一组正交函数集

1 第四章 连续系统的频域分析 §4-1 信号分解为正交函数 一.正交函数和正交函数集 1.正交矢量 C12 V2 V1 cos θ G G = 2 1 2 2 2 1 cos V V V V V V G G G G G G ⋅ = = θ θ → C12 V2 → V1 → V2 2 2 1 2 12 V V V C K G G ⋅ = 当 ， 完全重合，则 随着夹角θ增大， 减小； 当 ， 和 相互垂直 V1 G V2 G 0, 1 θ = c12 = 12 c 90 , 0 = c12 = o θ V1 G V2 G A C1vx C2vy G G = + A C x C y C z v v v 1 2 3 G G G = + + a. 平面, x、y正交坐标系 令 vx : x方向正交单位矢量 G 令 v y : y方向正交单位矢量 G b. 三维, x、y、z正交坐标系 {v ,v ,v } x y z G G G 正交矢量集 0, i j Vi ⋅Vj = ≠ G G i i i V ⋅V =k G G c. 一般: A CV CV Cn Vn G " G G 矢量: = 1 1 + 2 2 + + Cm为A在Vm中的投影 G 2 m m m V A V C G G ⋅ = 2. 正交函数 ( ) ( ) 0 2 1 1 2 = ∫ t t dt t t ϕ ϕ ( ) ( ) (t , t ) . 则称 ϕ 1 t 和ϕ 2 t 在区间 1 2 内正交 ( , ) ( ) ( ) 1 2 1 2 定义：在 t t 区间内，若函数ϕ t 和ϕ t 满足 3. 正交函数集 = ∫ t t dt t t j 2 1 ( ) ( ) ϕi ϕ k i j i j i ≠ = ≠ 0 0 . ( , ) 1 2 函数集 称此函数集是 t t 区间上一组正交 ( ) ( ) ( ) 1 2 n t t t 定义：若 个函数ϕ ，ϕ ，"，ϕn 构成一个函数集,且在区间（t 1,t2 )内满足 ①正交函数集

②完备的正交函数集③信号分解为正交函数如果(9,(1),,(t),,甲,(t)是一组正交函数集,f(t)在(t,t,)有定义,f(t)可近似表示为且对任意v(t)m(t),m=1,2, ,n,不存在F()C()+c9()++c,,(t)-Zc,(t)'v(0).()dt=0 (m=1,, n)均方误差称此函数集为完备正交函数集.(-e0(0d2=t -t, Ja?令=0J'y'(t) d :ckac.i=禁务's(0)g,(0)dtk,=I'ojdt得cj ='o;(t)dt此时()=Ci()+c9(t)++c,甲,(t)+..4.常用正交函数集若n→,=0,得①三角函数集(cos no,t,sinno,t) n=0,±1,+2..②复指数函数集$4-2付立叶级数与周期信号的频谱(eina")n = 0,±1,±2....周期信号r(t)满足Dirichlet条件时，在区间（to,t+T)可以展开成在完备正交信号③勒让德多项式空间中的无穷级数。如果完备的正交函④切比雪夫多项式数集是三角函数集或指数函数集，那么，周期信号所展开的无穷级数，就分③沃尔什函数别称为“三角形付立叶级数"或“指数形式付立叶级数，统称为付立叶级数

2 ②完备的正交函数集 { ( ), ( ), , ( )} , 如果 ϕ 1 t ϕ 2 t " ϕ n t 是一组正交函数集 ( ) ( ) 0 ( 1,2, , ) 2 1 t t dt m n t t ∫ ψ ϕ m = = " 称此函数集为完备正交 函数集. 且对任意 ψ(t) ≠ϕ m(t),m = 1,2,",n, 不存在 ∑= ≈ + + + = n j n n j j f t c t c t c t c t 1 1 1 2 2 ( ) ϕ ( ) ϕ ( ) " ϕ ( ) ϕ ( ) ③信号分解为正交函数 f (t)在(t1 , t2 )有定义 , f (t)可近似表示为 f t c t dt t t n j j j t t 2 1 2 1 2 [ ( ) ( )] 1 2 ∫1 ∑= − − ε = ϕ 均方误差 0 2 = ∂ ∂ j c ε 令 ∫ ∫ = 2 1 2 1 ( ) ( ) ( ) 2 t t j t t j j t dt f t t dt c ϕ ϕ 得 若 n → ∞,ε2 = 0, 得 k dt t t j = ∫ j 2 1 2 ϕ ∫ ∑ ∞ = = 1 2 2 2 1 ( ) j j j t t f t dt c k 帕斯瓦 尔方程 此时 f (t) = c1 ϕ1 (t) + c2ϕ 2 (t) +"+ cnϕ n (t) +" 4. 常用正交函数集 {cos nω1t,sin nω1t} n = 0,±1,±2" ①三角函数集 {e jnω1t } n = 0,±1,±2" ②复指数函数集 ③勒让德多项式 ④切比雪夫多项式 ⑤沃尔什函数 §4-2付立叶级数与周期信号的频谱 周期信号f(t)满足Dirichlet条件时，在 区间（t0,t0+T)可以展开成在完备正交信号 空间中的无穷级数。如果完备的正交函 数集是三角函数集或指数函数集，那 么，周期信号所展开的无穷级数，就分 别称为“三角形付立叶级数”或“指数形式 付立叶级数”，统称为付立叶级数

傅里叶生平一.付立叶级数的三角函数形式·1768年生于法国1.付立叶级数展开·1807年提出“任何(0)=%+a. cos nQt+Zb. sin nQt运周期信号都可用正弦函数级数表示”Q=2元·1822年首次发表α=号 ()dl 直流分量“热的分析理论”f" f(t)cos nQtdta.=TJ2rT f(t)sin nQtdtb.:AT.a.o.(0=+2A.cos(n21+9.)及b.n=2.几种特殊形式的付氏级数其中A= A=+,=arctan①奇函数：关于原点对称,f(-1)=-f(0)a.if(t)②偶函数:关于纵轴对称(-1)=f(0)f(t)仅有正弦分量即a=0 a.=0无正弦级数分量,即b,=0f(t)=-Z b, sin nQ21(0)=%+2 a. cosn21n=l

3 傅里叶生平 • 1768年生于法国 • 1807年提出“任何 周期信号都可用正 弦函数级数表示” • 1822年首次发表 “热的分析理论” 一.付立叶级数的三角函数形式 1. 付立叶级数展开 T 2π Ω = ∑ ∑ ∞ = ∞ = = + Ω + Ω n 1 1 n n n 0 cos n sin n 2 ( ) a t b t a f t = ∫ 直流分量 T f t dt T a 0 0 ( ) 2 = ∫ Ω T f t tdt T a 0 n ( ) cos n 2 = ∫ Ω T f t tdt T b 0 n ( )sin n 2 A cos(n ) 2 A ( ) n n 1 n 0 = +∑ Ω +ϕ ∞ = 及 f t t 其中 ) a b A A , arctan( n n n 2 n 2 0 = a0 n = an +b ϕ = − A n bn n a ϕ n ①奇函数:关于原点对称, f (−t) = − f (t) 2. 几种特殊形式的付氏级数 仅有正弦分量,即a0 = 0 an = 0 f t = ∑ Ωt ∞ = ( ) b sin n n 1 n t f (t ) f t a t a = +∑ Ω ∞ = ( ) cosn n 1 2 n 0 t f (t) ②偶函数: 关于纵轴对称, f (−t) = f (t) 无正弦级数分量 ,即bn = 0

④偶谐波函数③奇谐波函数 f(t+)=-f(t)(t)f(t)只有奇次谐波1- af(t)=Z A2n-COS(2n-1)2t+ @2m-1 2n=lk = 1,2,3,4 3、信号的分解二、付立叶级数的指数（复数）形式奇函数部分偶函数部分由欧拉公式2f(t)= foa(t)+ fa(t)Sin nQt = e/ml-e'm2jf(-t)=-foa(t)+ fe(t): 1.(0)-10--0.()-10+- emai + e-/na!cos nQt =222b.,+ ja,em +e-moyF.:(a, +jb.)f(0)=%+Zar2jC6-9令+2b.(e/nare-jn2t)122Ddf(0)=F +2F,ern jn2F.e=+2(=ihena ++ibhem)n=122l2ZF.ero二Fa=2(a.-Jb)=1A.eno=-0

4 ) ( ) 2 ( f t T ③奇谐波函数 f t ± = − f(t) t ( ) A COS[(2n 1) ] 2n 1 n 1 2n 1 − ∞ = f t =∑ − − Ωt +ϕ k = 1 ,2 ,3 ,4 " 只有奇次谐波 f (t) t ④偶谐波函数 A Cos(2n ) 2 A ( ) 2n n 1 2n 0 = +∑ Ω +ϕ ∞ = f t t f (t) f (t) f (t) = od + ev 奇函数部分 偶函数部分 f ( t) f (t) f (t) − = − od + ev 3、信号的分解 2 ( ) ( ) ( ) 2 ( ) ( ) ( ) f t f t f t f t f t f t od ev + − = − − ∴ = j e e t j t j t 2 sin n nΩ − nΩ − Ω = 2 cos n jn t jn t e e t Ω − Ω + Ω = 二. 付立叶级数的指数(复数)形式 由欧拉公式 2 2 ( ) n n n 1 n 0 j t j t e e a a f t ∞ Ω − Ω = + = +∑ ∑ ∞ = Ω + − Ω + − = + n 1 0 n n n n n n ) 2 2 ( 2 j t j t e a jb e a a jb ( ) 2 1 n n n 1 n j t j t e e j b Ω − Ω ∞ = +∑ − n j n n n n A e 2 1 ( ) 2 1 ϕ 定义 F = a − jb = ( ) 2 1 2 n n n n n a jb j b ja F = + + = − − − 2 0 0 a 令 F = j t j t f t F F e F e− Ω ∞ = − Ω ∞ = = +∑ +∑ n n 1 n n n 1 0 n ( ) j t F e Ω ∞ = −∞ = ∑ n n n

其中IF.l～nQ波形幅值频谱P,~n相位频谱e-manaF,=(a.- jb.)=uL/(0)例：如图三.周期信号的频谱ZF,en!f(t)=n=-0解 F,=,ume-mard↑[F. ]Ume-jno'dt ]nd-20-Q2202ume-号Pnn = 0,±1,±2....元(n2)0.号2umF,/ =n = 0,±1,±2...-20-2220n2元(n2)]付立叶变换一非周期信号的频谱小结：$4-3信号频谱的特点①离散性一，非周期信号频谱的特点②谐波性(间隔为 α整数倍)1f0)③收敛性中-tt10)曼.中

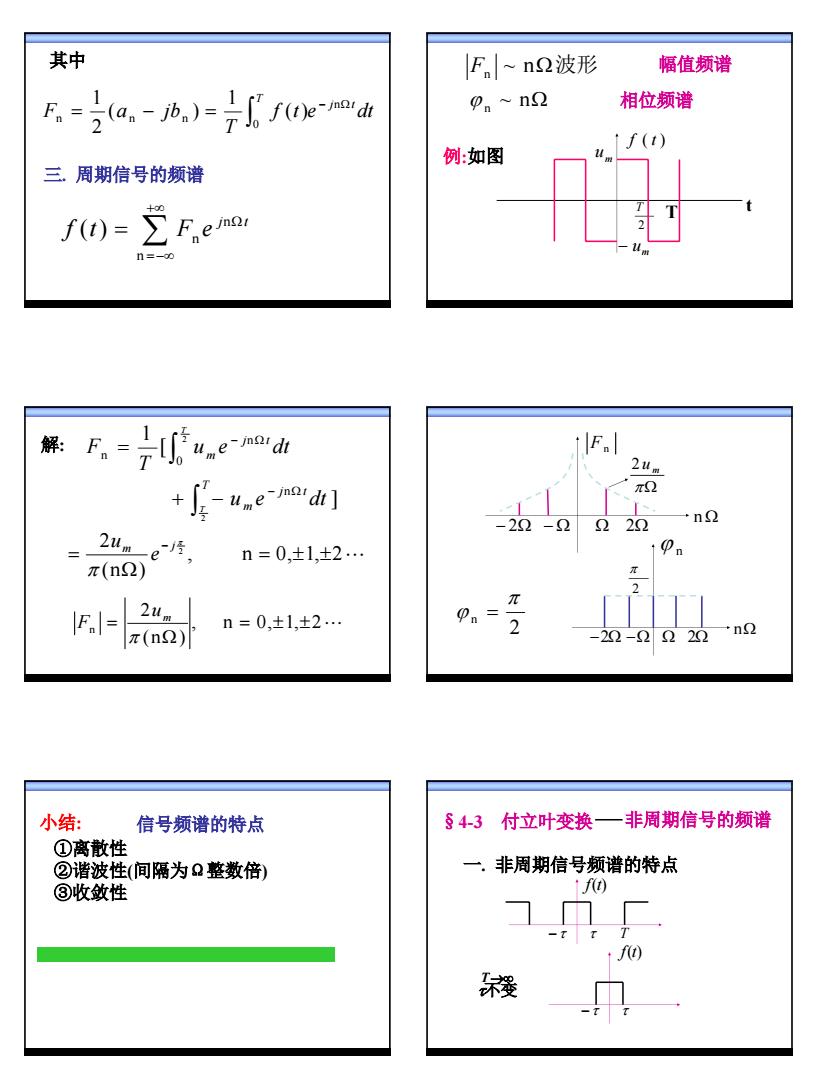
5 f t e dt T F a jb j t T − Ω ∫ = − = n 0 n n n ( ) 1 ( ) 2 1 其中 ∑ +∞ = −∞ Ω = n n n ( ) j t f t F e 三. 周期信号的频谱 Fn ~ nΩ波形 幅值频谱 ϕ n ~ nΩ 相位频谱 T 2 T t − um m u f ( t ) 例:如图 ] 2 n u e dt T j t ∫T m − Ω + − u e dt T F T j t ∫ m − Ω = 2 0 n n [ 1 解: , n 0, 1, 2" (n ) 2 2 = ± ± Ω = − π π m j e u , n 0, 1, 2" (n ) 2 n = ± ± Ω = π m u F − 2Ω − Ω Ω 2Ω Fn πΩ m 2u n Ω 2 n π ϕ = −2Ω −Ω Ω 2Ω ϕ n 2 π nΩ 信号频谱的特点 ①离散性 ②谐波性(间隔为Ω整数倍) ③收敛性 小结: §4-3 付立叶变换 非周期信号的频谱 f(t) −τ τ T f(t) −τ τ T→∞ τ不变 一. 非周期信号频谱的特点