
第19章分布参数的电路 §1.分布参数和分布参数电路 实际电路中参数具有分布性,必须考虑参数分布性的电路, 称为分布参数电路。 + 例:室内1500m电线 u u2 f=50 Hz 3×108 =6000km 1500m f50 延时时间 t'≤1500 3×108 =5×106s u =Um sin 100t 42=Um sin100元(t-0.000005) =U sin(100πt-0.0005π) U1≈u2 =U sin(100πt-0.09) 1500m的输电线处理为集总参数电路
例 : 室内1500m电线 f =50 Hz 6000 km 50 3 108 = = = f v u1 u2 1500m + + - - 1500m的输电线处理为集总参数电路 延时时间 5 10 s 3 10 1500 6 8 − = t = u U sin100 t 1 = m sin(100 0.09 ) sin(100 0.0005 ) sin100 ( 0.000005) m m 2 m = − = − = − U t U t u U t u1 u2 § 1.分布参数和分布参数电路 第19章 分布参数的电路 实际电路中参数具有分布性,必须考虑参数分布性的电路, 称为分布参数电路

1500km的输电线 + u 延时时间 1-150000-5×10s 0 3×108 1500km 41=Um sin100πt 4,=U sin10(0x(t-0.00s)=U sin(100元t-〉 1500km的输电线处理为分布参数电路
u U sin100 t 1 = m ) 2 2 m sin100 ( 0.005) m sin(100 u = U t − = U t − 1500km的输电线处理为分布参数电路 1500km的输电线 u1 u2 1500km + + 延时时间 - - 5 10 s 3 10 1500000 3 8 − = t =
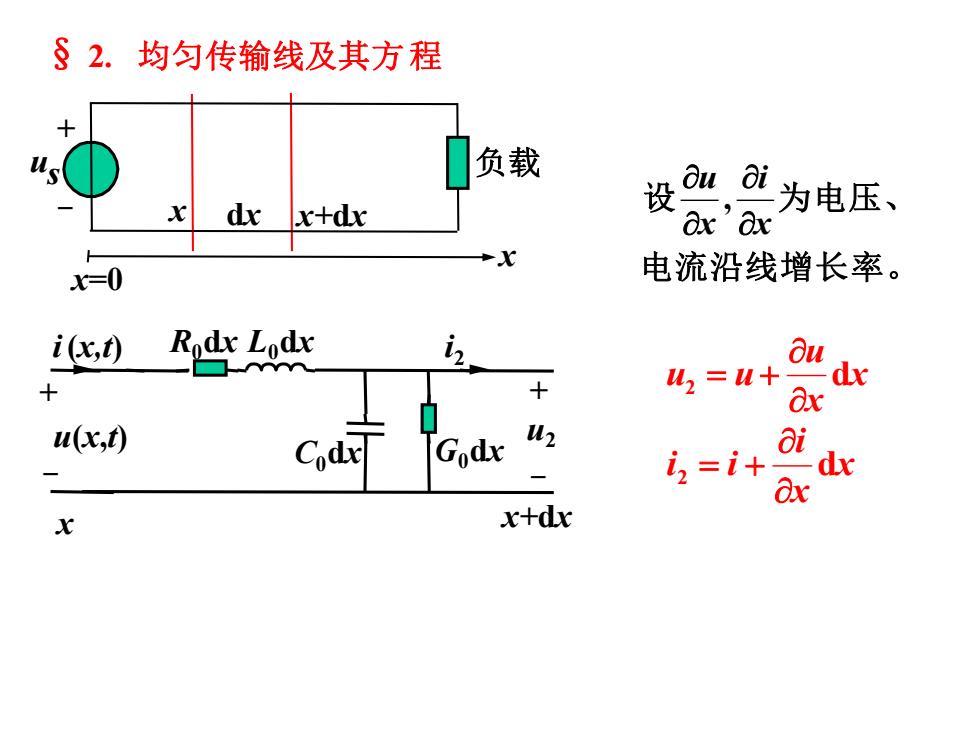
§2.均匀传输线及其方程 负载 dx x+dx oui为电压、 Ox'ax X=0 电流沿线增长率。 i(x,t) Rodx Lodx - 3u + u2=W+ dx ax u(x,t) Codx Godx W2 ai 2=i+ o dx Ox X x+dx
电流沿线增长率。 设 为电压、 x i x u , x x i i 2 i d = + x x u u2 u d = + x dx x+dx x us 负载 + - x=0 i2 x C G0dx 0dx R0dx L0dx u2 i(x,t) u(x,t) x+dx + - - + § 2. 均匀传输线及其方程
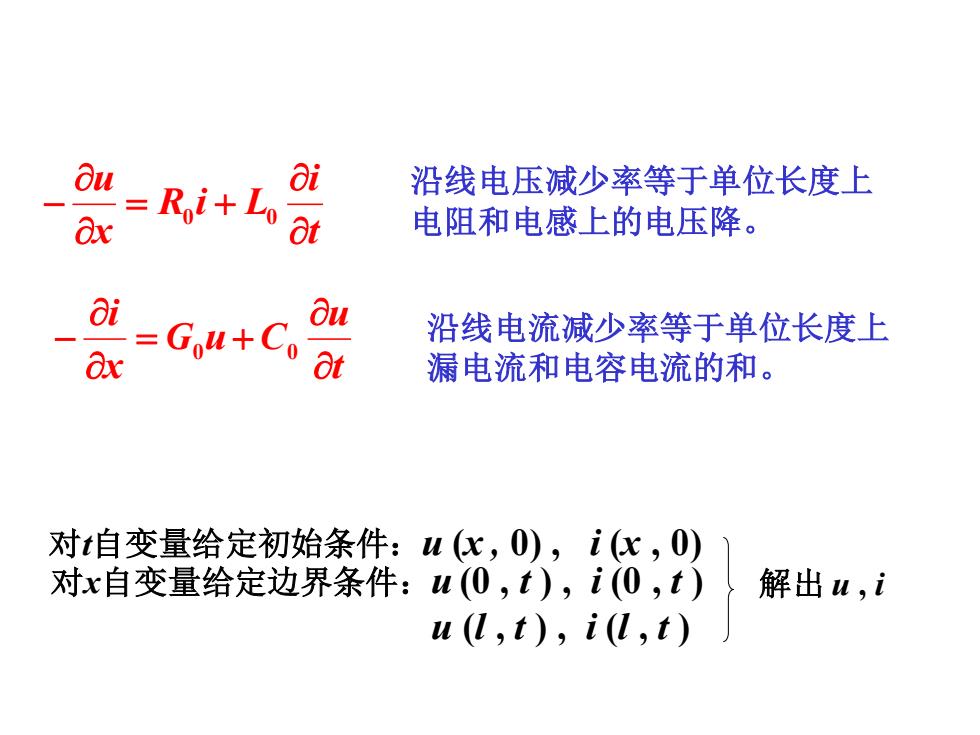
ou = 0i 沿线电压减少率等于单位长度上 Ex Roi+Lo 8t 电阻和电感上的电压降。 Oi &x =Gou+Co Ou 沿线电流减少率等于单位长度上 Ot 漏电流和电容电流的和。 对t自变量给定初始条件:u(c,O),i(c,0) 对x自变量给定边界条件:u(0,t),i(0,t) 解出u,i u(l,t),i(l,t)
t i R i L x u = + − 0 0 沿线电压减少率等于单位长度上 电阻和电感上的电压降。 t u G u C x i = + − 0 0 沿线电流减少率等于单位长度上 漏电流和电容电流的和。 对t自变量给定初始条件:u (x , 0) , i (x , 0) 对x自变量给定边界条件:u (0 , t ) , i (0 , t ) u (l , t ) , i (l , t ) 解出 u , i

§3均匀传输线的正弦稳态解 一.相量方程 us =Um sin at i(x,t) u=v2U(x)sin(at+v,(x)) ① u(x,t) i=2I(x)sin(at+v;(x)) t=0 有效值和初相位是位移x的函数 u(x,t)-→U(x) i(x,t)→1(x) 简记为:0,1
u U t S = m sin 2 ( )sin( ( )) 2 ( )sin( ( )) i I x t x u U x t x i u = + = + U I 简记为: , § 3 均匀传 输线的正弦稳态解 一. 相量方程 t=0 x us u(x,t) i(x,t) + - + - u(x,t) U(x) → i(x,t) I(x) → 有效值和初相位是位移 x 的函数