
第九章 正弦稳态电路的分析
第九章 正弦稳态电路的分析

第九章 正弦稳态电路的分析 §9-1阻抗和导纳 §9-2阻抗(导纳)的串联和并联 § 9一3电路的相量图 § 9一4正弦稳态电路的分析 § 9一5正弦稳态电路的功率 9一6功率因数的提高 §9-7最大功率传输 § 9一8串联电路的谐振 § 9一9并联谐振电路 2-2
第九章 正弦稳态电路的分析 2-2 § 9-1 阻抗和导纳 § 9-2 阻抗(导纳)的串联和并联 § 9-3 电路的相量图 § 9-4 正弦稳态电路的分析 § 9-5 正弦稳态电路的功率 § 9-6 功率因数的提高 § 9-7 最大功率传输 § 9-8 串联电路的谐振 § 9-9 并联谐振电路

§9一1阻抗和导纳 阻抗和导纳的概念以及对它们的运算和等效变换是线性电 路正弦稳态分析中的重要内容。 一.复数阻抗Z: 下图(a)所示为一个含线性电阻、电感和电容等元件, 但不含独立源的一端口N。 当它在角频率为ω的正弦电压(或正弦电流)激励下处于 稳定状态时,端口的电流(或电压)将是同频率的正弦量 应用相量法,端口的电压相量)与电流相量的比值定义为 该一端口的阻抗Z(又叫等效阻抗输入阻抗,驱动点阻抗)。 No 等效 图(a)
等效 Z U I I U Z = § 9-1阻抗和导纳 阻抗和导纳的概念以及对它们的运算和等效变换是线性电 路正弦稳态分析中的重要内容。 一.复数阻抗 Z: 下图(a)所示为一个含线性电阻、电感和电容等元件, 但不含独立源的一端口N0。 当它在角频率为的正弦电压(或正弦电流)激励下处于 稳定状态时,端口的电流(或电压)将是同频率的正弦量。 I 应用相量法 U ,端口的电压相量 与电流相量 的比值定义为 该一端口的阻抗 Z(又叫等效阻抗,输入阻抗,驱动点阻抗)。 I U N0 图(a)
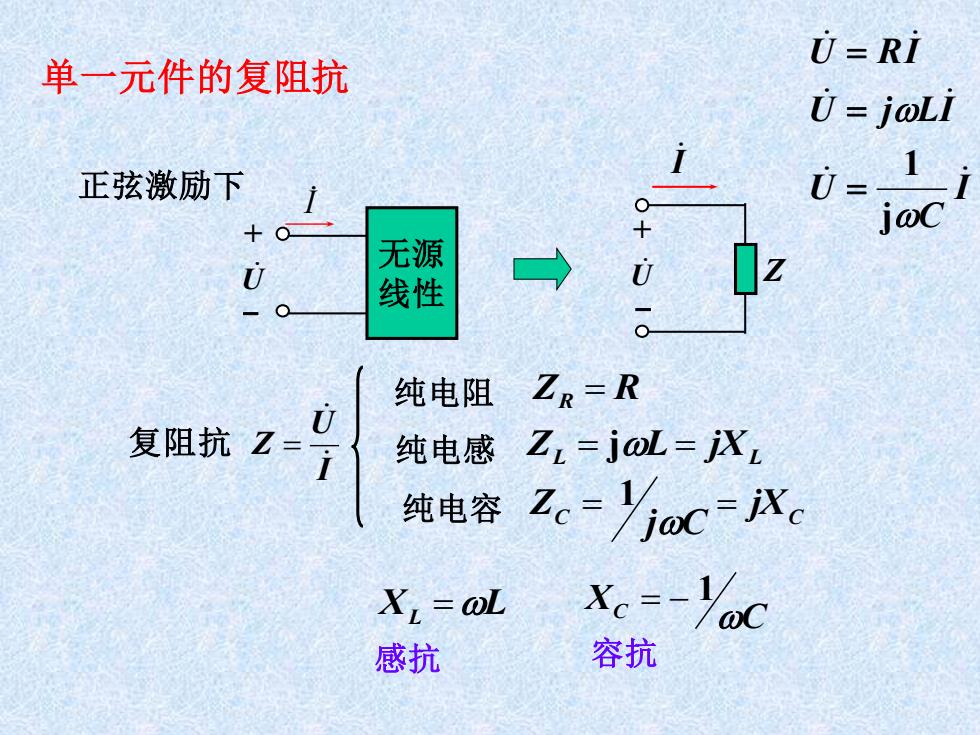
U-RI 单一元件的复阻抗 U=joLi 正弦激励下 0= 1 jwC 无源 线性 纯电阻 ZR=R 复阻抗Z= 纯电感 Z=joL=iX 纯电容 Ze-Yjoc=Xc X:.=@L X=-%c 感抗 容抗
C XC = − 1 单一元件的复阻抗 正弦激励下 I U Z + - 无源 线性 I U + - I U Z 复阻抗 = 纯电阻 ZR = R L L 纯电感 Z = jL = jX C C jX j C Z = = 纯电容 1 XL =L 感抗 容抗 I C U U j LI U RI j 1 = = =

(1)Z和总电流、总电压的关系 由复数形式的欧姆定律心=☑ 可得: U 84k。片Q-只是 Z=140. 电阻 电抗 阻抗模: 阻抗角: P2=p-0 结论:Z的模为电路总电压和总电流有效值之比, 而Z的幅角则为总电压和总电流的相位差。 阻抗适合于串联电路的计算,单位是欧姆
由复数形式的欧姆定律 U = I Z 可得: 结论:Z的模为电路总电压和总电流有效值之比, 而Z的幅角则为总电压和总电流的相位差。 (1)Z 和总电流、总电压的关系 I U 阻抗模: Z = Z =u −i 阻抗角: R j X I U Z I U I U Z Z u i i u = = − = + = = 电阻 电抗 阻抗适合于串联电路的计算,单位是 欧姆