
② iz [ 0 ③ is 4 4 is ④ i1-i4+6 -i,-2+§ =0 i2+i3-6 矩阵形式的KCL Ai=0
矩阵形式的KCL Ai = 0 2 3 6 1 2 5 1 4 6 = + − − − + − + = i i i i i i i i i -1 -1 0 0 1 0 1 0 0 -1 0 1 0 1 1 0 0 -1 6 5 4 3 2 1 i i i i i i 6 4 5 3 2 1 ① ② ④ ③ A i = 0

② 矩阵形式KVL 2 5 ③ 4 3 0 Unl Un2 ④ 0 Un2 +Un3 W2 0 W Un3 3 -1 0 Wn2 一unl M4 0 0 Un2 5 0 Unl Un3 6
矩阵形式KVL = − − − +− = 1 3 2 1 3 2 3 1 2 n n n n n n n n n u u uuu u u u u uuuuuu654321 − − −− 321 1 0 1 0 1 0 1 0 0 0 0 1 0 1 1 1 1 0 nnn uuu un = u T A 6 4 5 3 2 1 ① ②④ ③

回路矩阵 回路与支路的关系。 矩阵的行对应回路,列对应支路,矩阵中的元素值 为-1,0,1 0表示对应的支路不在相应回路中 -1表示对应的支路不在相应的回路中,支路电流 与回路电流的参考方向相反 1表示对应的支路在相应的回路中,支路电流与 回路电流的参考方向一致
回路矩阵 回路与支路的关系. 矩阵的行对应回路,列对应支路,矩阵中的元素值 为-1,0,1 0表示对应的支路不在相应回路中 -1表示对应的支路不在相应的回路中,支路电流 与回路电流的参考方向相反 1表示对应的支路在相应的回路中,支路电流与 回路电流的参考方向一致
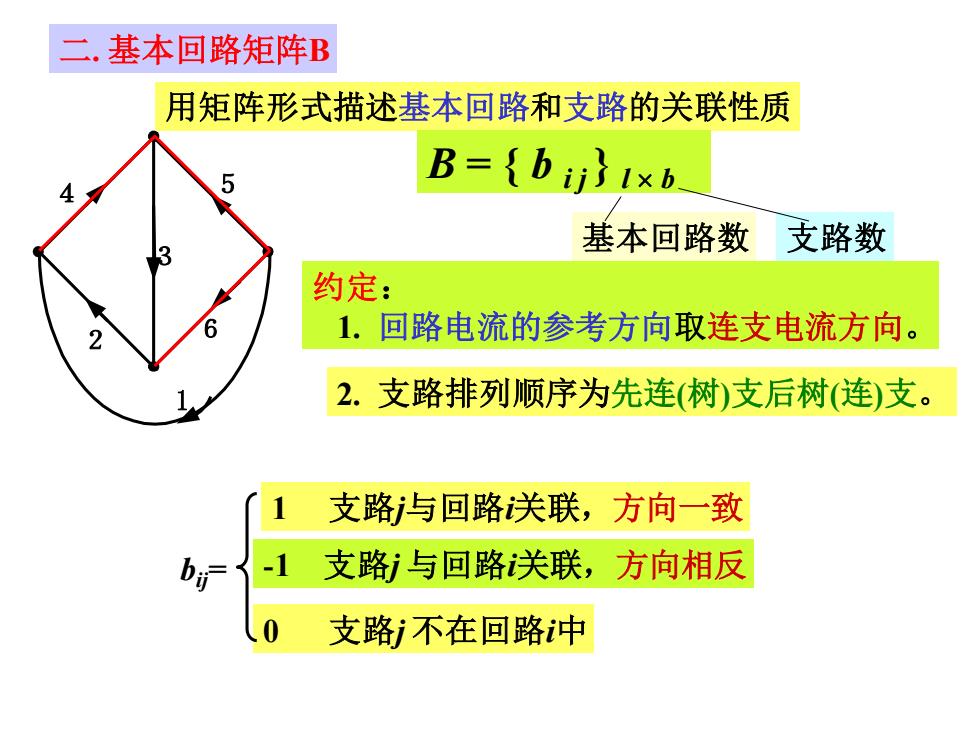
二.基本回路矩阵B 用矩阵形式描述基本回路和支路的关联性质 B=bij)1xb 基本回路数 支路数 约定: 2 6 1.回路电流的参考方向取连支电流方向。 2.支路排列顺序为先连(树)支后树(连)支。 支路与回路关联,方向一致 b 支路与回路关联,方向相反 支路不在回路中
二. 基本回路矩阵B 2. 支路排列顺序为先连(树)支后树(连)支。 1 支路j与回路i关联,方向一致 -1 支路j 与回路i关联,方向相反 0 支路j 不在回路i中 bij= 1 2 3 6 4 5 约定: 1. 回路电流的参考方向取连支电流方向。 用矩阵形式描述基本回路和支路的关联性质 B = { b i j } l b 基本回路数 支路数
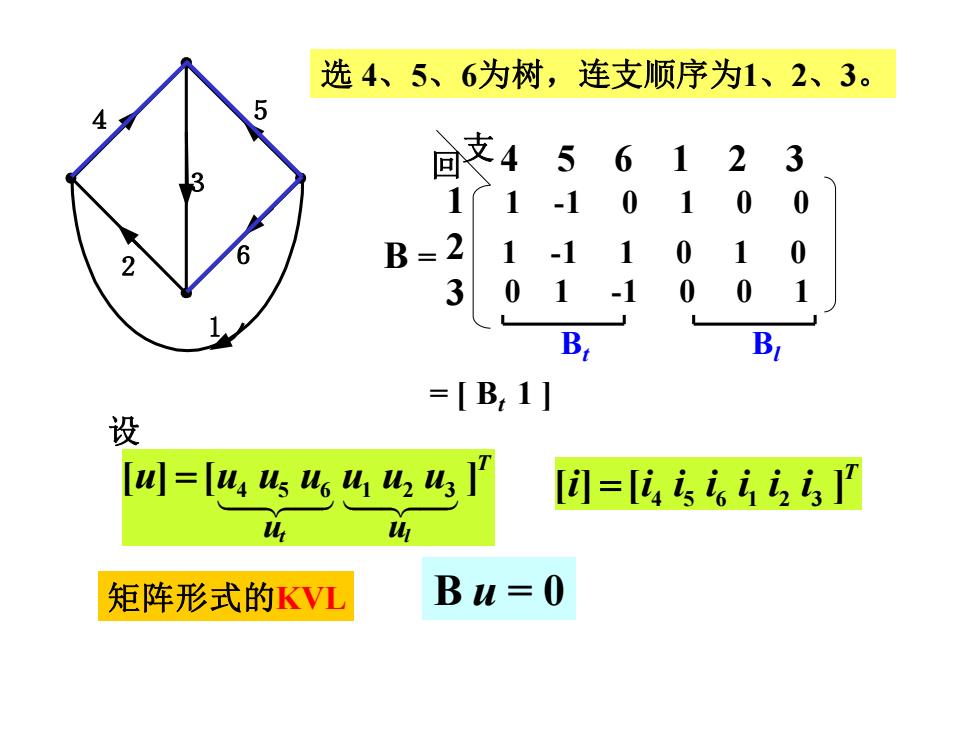
选4、5、6为树,连支顺序为1、2、3。 5 回支45612 3 11-1 0 1 0 0 6 B=2 1-1 1 0 3 01 -1 0 0 B, B =[B,1] 设 [四=[w45u641h24 [川=[6g,123 % 西 矩阵形式的KVL Bu=0
1 2 3 6 4 5 选 4、5、6为树,连支顺序为1、2、3。 1 2 3 B = 回 支4 5 6 1 2 3 1 -1 0 1 0 0 1 -1 1 0 1 0 = [ Bt 1 ] 设 T [i] [i i i i i i ] = 4 5 6 1 2 3 矩阵形式的KVL T ut ul [u] [u u u u u u ] = 4 5 6 1 2 3 0 1 -1 0 0 1 Bt Bl B u = 0