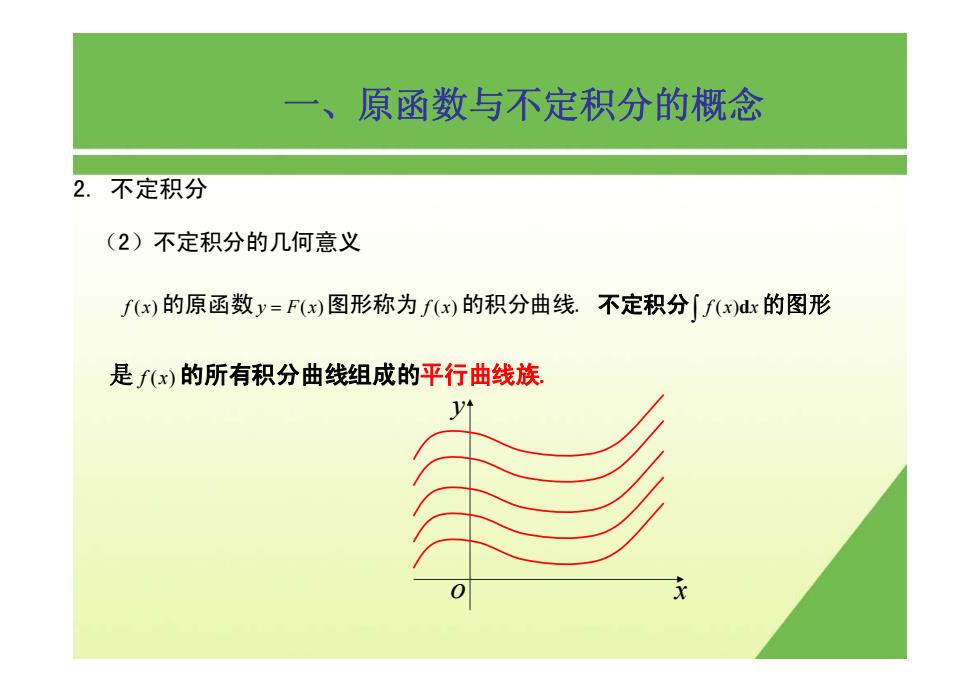
一、原函数与不定积分的概念 2. 不定积分 (2)不定积分的几何意义 fx)的原函数y=F(x)图形称为f)的积分曲线.不定积分[fx)dr的图形 是f(x)的所有积分曲线组成的平行曲线族 X
(2)不定积分的几何意义 f ( ) x 的原函数y Fx = ( )图形称为 f ( ) x 的积分曲线. 不定积分 f ( ) x x ∫ d 的图形 2. 不定积分 是 f ( ) x 的所有积分曲线组成的平行曲线族. 一、原函数与不定积分的概念 y o x
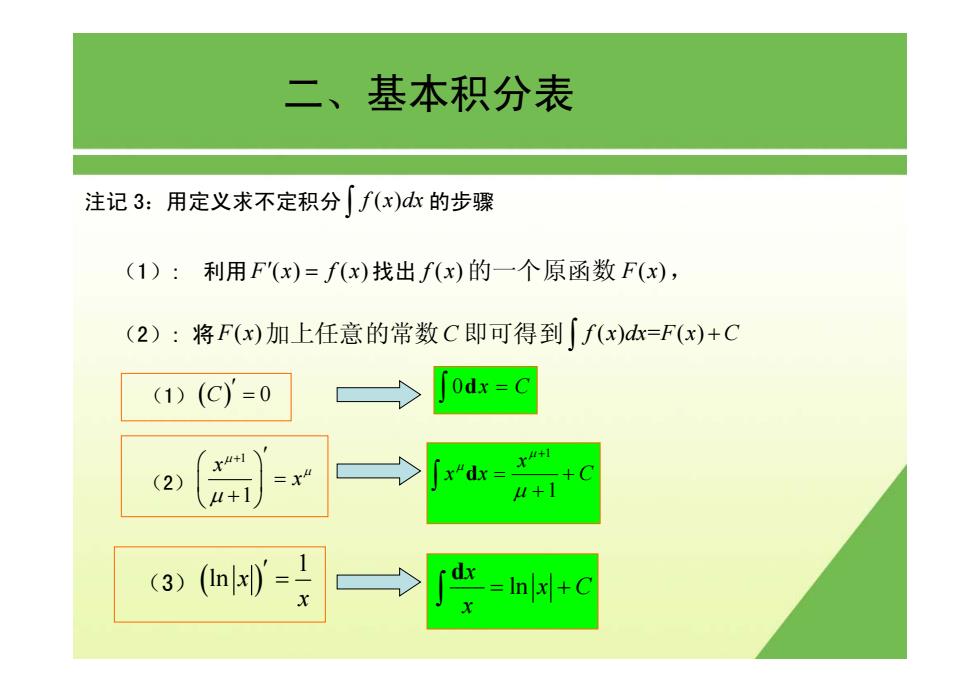
二、基本积分表 注记3:用定义求不定积分∫f(x)dk的步骤 (1):利用F'(x)=f(x)找出f(x)的一个原函数F(x), (2):将F(x)加上任意的常数C即可得到f(x)d=F(x)+C (1)(C)=0 0dx=C (2) x"dx= A+1 (3)(=1
注记 3:用定义求不定积分 f x dx ( ) ∫ 的步骤 (1): 利用Fx fx ′() () = 找出 f ( ) x 的一个原函数 F x( ), (2): 将F x( )加上任意的常数C 即可得到 f () = () x dx F x C+ ∫ 二、基本积分表 (1)(C) 0 ′ = (2) 1 1 x x μ μ μ + ′ ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ + (3)( ) 1 ln x x ′ = 0 x C = ∫ d 1 1 x xx C μ μ μ + = + + ∫ d ln x x C x = + ∫ d
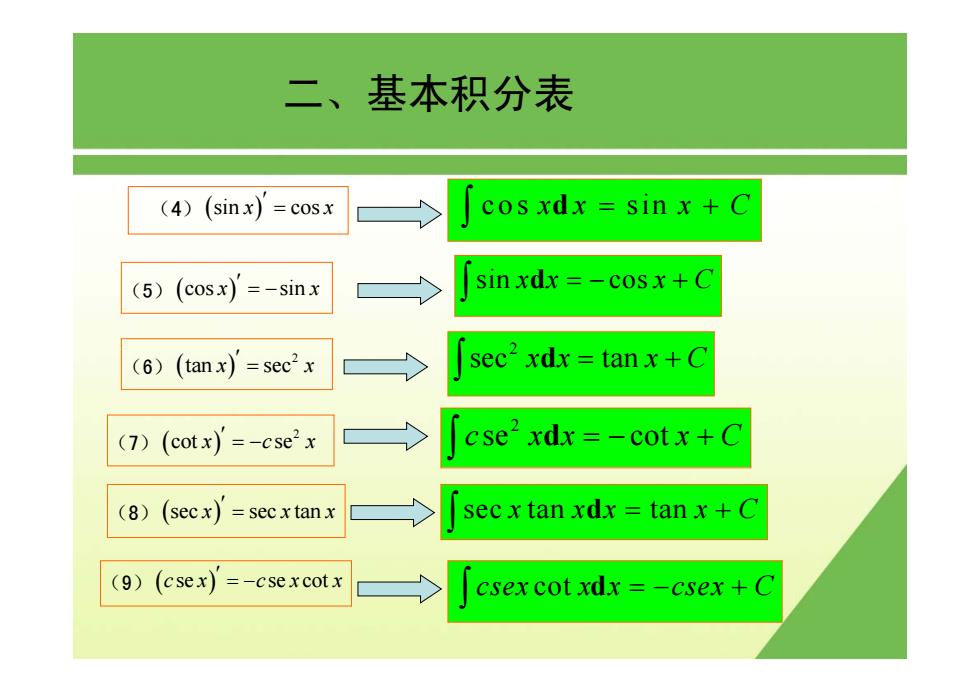
二、基本积分表 (4)(sinx)=cosx cosxdx sin x +C (5)(cosx)'=-sinx sin xdx =-cosx+C (6)(tanx)=sec2x sec2 xdx tanx+C (7)(cotx)'=-cse2x cse xdx=-cotx+C (8) (secx)'=secxtanx secx tan xdx tanx+C (9)(csex) =-csexcotx csex cot xdx =-csex +C
二、基本积分表 (4)(sin cos x x )′ = (5)( ) cos sin x x ′ = − cos sin xx x C = + ∫ d sin cos xx x C =− + ∫ d (6)( ) 2 tan sec x x ′ = 2 sec tan xx x C = + ∫ d (7)( ) 2 cot se x cx ′ = − 2 c xx x C se cot = − + ∫ d (8)( ) sec sec tan x xx ′ = sec tan tan x xx x C = + ∫ d (9)(cx cx x se se cot )′ = − csex x x csex C cot = − + ∫ d
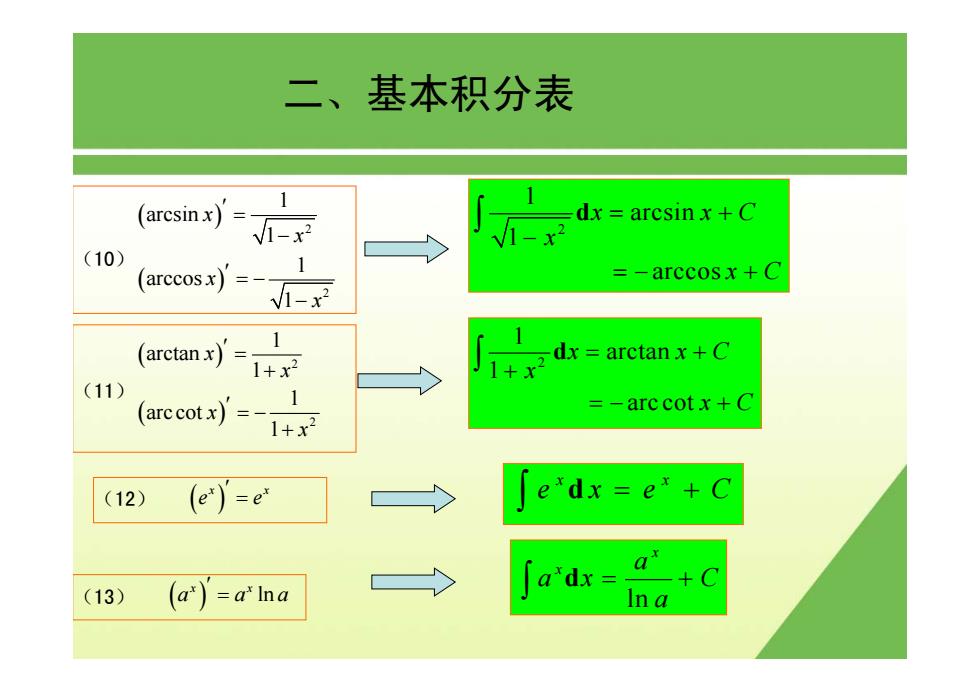
二、基本积分表 (arcsinx)=1 dx arcsinx+C √-x2 V1-x2 (10) 1 (arccosx)'=-- =-arccosx+C -2 (arctan.) 1+x2 dx arctanx+C 1+x (11) =-arc cotx+C 1+x2 (12) (e)'=e e*dx=e*+C a a*dx= (13) (a)=alna Ina
二、基本积分表 (10) ( ) ( ) 2 2 1 arcsin 1 1 arccos 1 x x x x ′ = − ′ = − − 2 1 arcsin 1 arccos x xC x x C = + − = − + ∫ d (11) ( ) ( ) 2 2 1 arctan 1 1 arc cot 1 x x x x ′ = + ′ = − + 2 1 arctan 1 arccot x x C x x C = + + = − + ∫ d (12) ( ) x x e e ′ = x x exe C = + ∫ d (13) ( ) ln x x a aa ′ = ln x x a ax C a = + ∫ d

三、不定积分的性质 性质1两个函数和的不定积分等于各个函数不定积分的和 「[fx)+gxdx=「f(x)dx+「g(x)dx 性质2:不为零的常数因子可以提到积分号外面. 分项积分 公式 ∫ro)ax=k灯f(x)dr 注记4若k,k2,,kn均为非零的常数,则 [k(x)±k36(x)±…±knf,(x)]dx=k,∫f(x)dx±k2∫f(x)dx±…±k∫f(x)dx
性质 1 两个函数和的不定积分等于各个函数不定积分的和 [ ( ) ( )] ( ) ( ) . f x gx x f x x gx x += + ∫ ∫∫ ddd 三、不定积分的性质 三、不定积分的性质 性质 2:不为零的常数因子可以提到积分号外面. kf x x k f x x () () = ∫ ∫ d d 分项积分 公式 注记 4 若 1 2 ,,, n kk k ⋅⋅⋅ 均为非零的常数,则 [ ] 11 2 2 () () () n n kf x kf x kf x x ± ±± ∫ " d 11 2 2 () () () . n n = ± ±± k f xxk f xx k f x x ∫∫ ∫ dd d