
导航 3.做一做:已知随机变量服从正态分布 N(2,o2)σ>0),P(6≤4)=0.84,则P(6≤0)等于( A.0.16 B.0.32 C.0.68 D.0.84 答案:A 解析:.随机变量服从正态分布N(2,62), .∴=2. 又P(64)=0.84, .∴P(≥4)=1-0.84=0.16, .∴.P(≤0)=P(24)=0.16
导航 3.做一做:已知随机变量ξ服从正态分布 N(2,σ 2 )(σ>0),P(ξ≤4)=0.84,则P(ξ≤0)等于( ) A.0.16 B.0.32 C.0.68 D.0.84 答案:A 解析:∵随机变量ξ服从正态分布N(2,σ 2 ), ∴μ=2. 又P(ξ≤4)=0.84, ∴P(ξ≥4)=1-0.84=0.16, ∴P(ξ≤0)=P(ξ≥4)=0.16

导 思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X” (I)函数p4x)中参数u,o的意义分别是样本的均值与方差 (2)正态曲线是单峰的,其与x轴围成的面积是随参数4,ō的变 化而变化的.( 3)正态曲线可以关于y轴对称(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“ ”,错 误的画“×” . (1)函数φμ,σ (x)中参数μ,σ的意义分别是样本的均值与方差. ( × ) (2)正态曲线是单峰的,其与x轴围成的面积是随参数μ,σ的变 化而变化的.( × ) (3)正态曲线可以关于y轴对称.( )
导航 课堂·重难突破 探究一正态曲线 【例1】一条正态曲线如图所示,试根据图象写出该正态分布 的密度函数解析式,求出总体随机变量的均值和方差 2元 510152025303540x
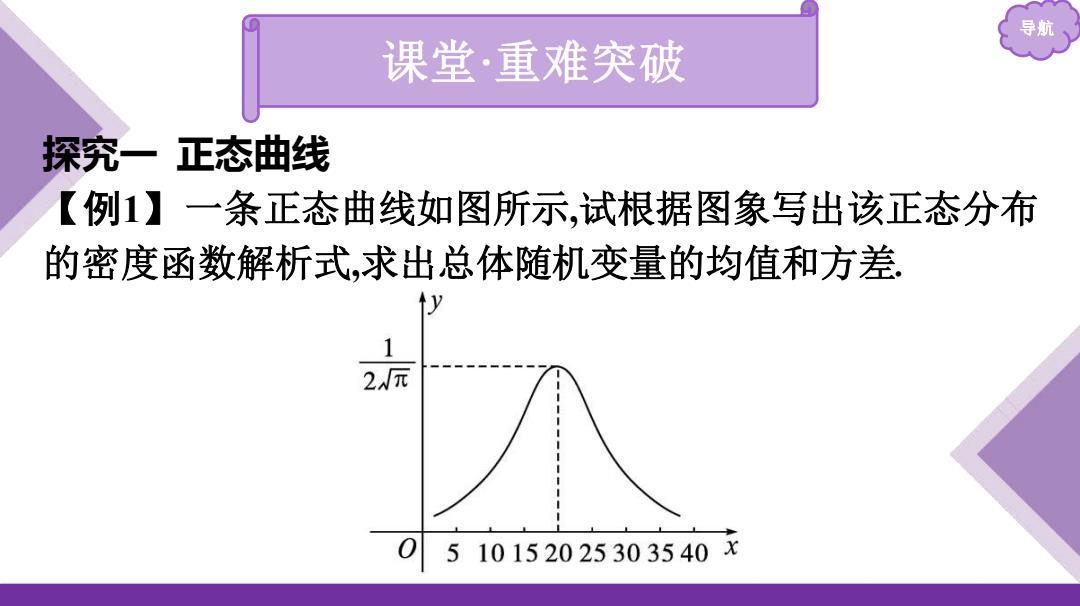
导航 课堂·重难突破 探究一 正态曲线 【例1】一条正态曲线如图所示,试根据图象写出该正态分布 的密度函数解析式,求出总体随机变量的均值和方差