
( =ker其中t为实变量 事实上设k=ax+iB,则 dek dt -e1=ee) _dt _dt dear iBt +ear de dt dt -aee4 (sin Bi+cos Bt) dt -ae(atip)+ea(-Bsin Bt+iB cos Bt) -ae +iBeaein=(a+iB)e=ke (3) 来er=4e 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 (2) 其中 为实变量 kt de kt ke dt = t 事实上,设 k i = + ,则 ( ) [ ] ( ) i t kt d d t i t e e de dt e dt dt + = = i t i t t de de t e e dt dt = + (sin cos ) t i t t d e e e t t dt = + + ( ) ( sin cos ) i t t e e t i t + = + − + ( ) kt t i t kt kt = + = + = e i e e i e ke (3) ( ) n kt n kt n d e k e dt =

现在我们引进线性方程的复值解的定义.定义于区间α≤t≤b 上的实变量复值函数x=(t)称为方程(4.1)的值解如果 0+a0+a产0 d"t du-2t +n-o8+a.00=0) 对于a≤t≤b恒成立. 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 现在我们引进线性方程的复值解的定义.定义于区间 上的实变量复值函数 称为方程 (4.1) 的值解如果 a t b x z t = ( ) ( ) 1 2 1 2 1 2 1 ( ) ( ) ( ) ( ) ( ) . ( ) ( ) ( ) ( ) n n n n n n n n d z t d z t d z t a t a t d t d t d t dz t a t a t z t f t dt − − − − − + + + + + 对于 a t b 恒成立.

定理8:如果方程(4.2)中所有系数4(t)(i=1,2,n) 都是实值函数,而x=z(t)=p(t)+i(t)是方程的复值 解,则z(的实部p(t),虚部和共轨复值函数 (t) 也都是方程(42)的解 证明设xz行=p(t)+()是方程(4.2)的复值解,则代入 方程得 [(t)+i(t)]+a (t)(t)+ig(t)]+ .+an(t)lp(t)+igp(t)]≡0 而1pm())+a,(t)pn-())+.+an()(川+ iLpm(t)+a,(t)pn-(t)+.+an(t)p(t川≡0 g((t)+a (t)o(-1()+.+a,()()]=0 由此得 pm)(t)+a1(t)pm-(t)+.+an(t)p(t)=0 结束 上一贡返回下页 首页
结束 帮助 上一页 返回 下一页 目录 首页 定理8:如果方程 中所有系数 都是实值函数,而 是方程的复值 解,则 的 和共轨复值函数 (4.2) ( )( 1,2,., ) a t i n i = x z t t i t = = + ( ) ( ) ( ) z t( ) 实部 ( ) ( ) t t ,虚部 z t( ) 也都是方程(4.2)的解. 证明:设 是方程(4.2)的复值解,则代入 方程得 x z t t i t = = + ( ) ( ) ( ) ( ) ( 1) 1 [ ( ) ( )] ( )[ ( ) ( )] n n t i t a t t i t − + + + + . . + + a t t i t n ( )[ ( ) ( )] 0 而 ( ) ( 1) 1 [ ( ) ( ) ( ) . ( ) ( )] n n n t a t t a t t − + + + + ( ) ( 1) 1 [ ( ) ( ) ( ) . ( ) ( )] 0 n n n i t a t t a t t − + + + 由此得 ( ) ( 1) 1 [ ( ) ( ) ( ) . ( ) ( )] 0 n n n t a t t a t t − + + + = ( ) ( 1) 1 ( ) ( ) ( ) . ( ) ( ) 0 n n n t a t t a t t − + + + =

由上面证明式说明中(利pt)的解),同理可证 (t)+i图的4.2) 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 也是 的解。 由上面证明式说明 ( )t 和 是 ( )t 的解 (4.2) ,同理可证 (4.2) ( ) ( ) t i t +
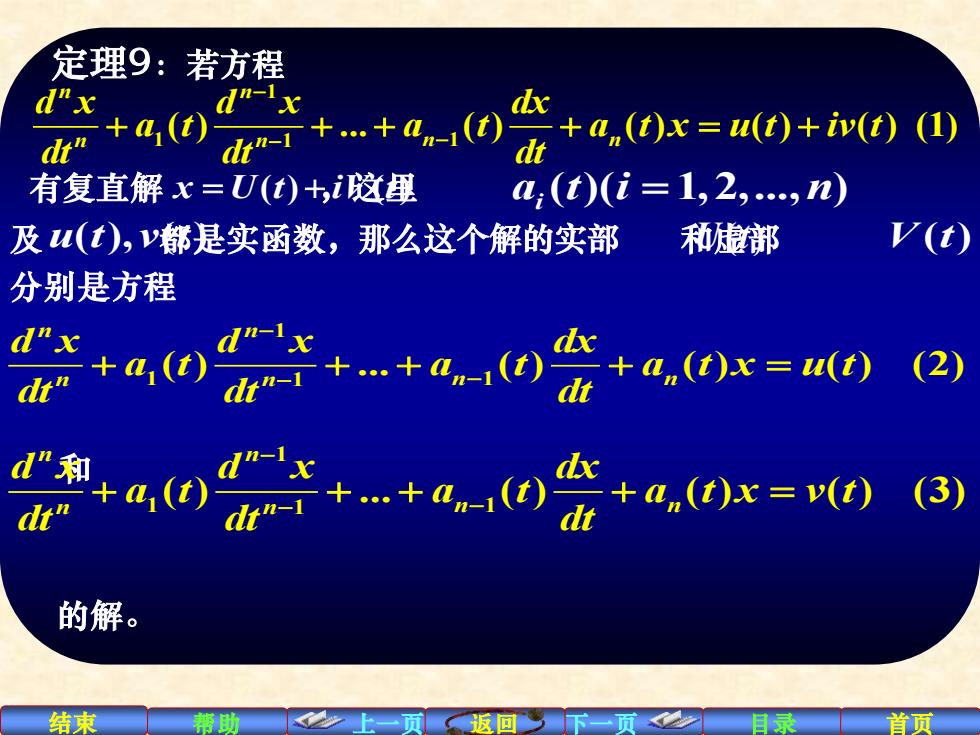
定理9:若方程 d"x d"-Ix dx +a(t) dt" dri+.+an-() +a,(t)x=u(t)+iv(t)(1) dt 有复直解x=U(t)+,这里 4,(t)(i=1,2,n) 及(t),都是实函数,那么这个解的实部 和虚部 V(t) 分别是方程 dx dt" )(2) )(3) 的解。 结束 上一贡扳同下一<2 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 和 1 1 1 1 ( ) . ( ) ( ) ( ) (3) n n n n n n d x d x dx a t a t a t x v t dt dt dt − + + + + = − − 的解。 1 1 1 1 ( ) . ( ) ( ) ( ) (2) n n n n n n d x d x dx a t a t a t x u t dt dt dt − + + + + = − − 定理9:若方程 1 1 1 1 ( ) . ( ) ( ) ( ) ( ) (1) n n n n n n d x d x dx a t a t a t x u t iv t dt dt dt − + + + + = + − − 有复直解 x U t iV t = + ( ) ( ) ,这里 ( )( 1,2,., ) a t i n i = 及 u t v t ( ), ( ) 都是实函数,那么这个解的实部 和虚部 U t( ) 分别是方程 V t( )