
§3.解对初值的连续性和 可微性 讲授内容:解对初值的连续性概念及解对 初值的连续性,可微性定理 讲授要点:解对初值的连续性定理 结束 助2上一贡返回下一页<2目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 §3. 解对初值的连续性和 可微性 讲授内容: 解对初值的连续性概念及解对 初值的连续性, 可微性定理 讲授要点: 解对初值的连续性定理

3.3解对初值的连续性和可微性 例:求方程 =y满足yx,)=的解。 d y=ce由y,=ce的满足y(x)=的解为y=ye- 说明解不仅是的函数,而且也是xo,'o的函数.所以 一般地初值问题 [y'=f(x,y) (2.1) y(x)=yo 的解,不仅依赖于x,同时也依赖于初值x) 因此,在初值变化的情况下,初值问题(2.1)的解是x,xo,y 的三元函数.记为 y=e(x,) 满足yo=p(X0,X0,yo) 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 例: 求方程 = 满足 的解 . dy y dx y x y ( ) 0 0 = 0 ( , ) (2.1) ( ) y f x y y x y = = x 0 0 ( , ) x y 0 0 x x y , , 的解,不仅依赖于 ,同时也依赖于初值 . 因此,在初值变化的情况下,初值问题(2.1)的解是 的三元函数.记为 = x y ce = 0 0 x y ce y x y ( ) 0 0 = − = 0 0 x x y y e 0 0 x y, 由 的满足 的解为 说明解不仅是 的函数,而且也是 的函数. 所以 一般地初值问题 x §3.3 解对初值的连续性和可微性 = 0 0 y x x y ( , , ) 满足 y x x y 0 0 0 0 =( , , )

3.3解对初值的连续性和可微性 解关于初值的一些基本性质 解关于初值的对称性: 设(2.1)满足y(x)=y的解是唯一的,记为 y=P(x,xo>Yo) 则在解的存在范围内,有y=p(x,x,y)成立. 事实上,在解的存在区间内任取一值x1,且记 =(x,x,o) 则由解的唯一性知,(x,y)过的解与过点(x1y)是同一条积 分曲线.即此解可表示为:y=p(x,七1,y1) 结束 上一贡返回下页<2 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 = 0 0 y x x y ( , , ) y x x y 1 1 0 0 =( , , ) 解关于初值的一些基本性质 解关于初值的对称性: 设(2.1)满足 y x y ( ) 0 0 = 的解是唯一的,记为 则在解的存在范围内,有 y x x y 0 0 =( , , ) 成立 . 1 事实上,在解的存在区间内任取一值 x ,且记 §3.3 解对初值的连续性和可微性 1 1 则由解的唯一性知, 过的解与过点 ( , ) x y 是同一条积 分曲线. 即此解可表示为: 0 0 ( , ) x y = 1 1 y x x y ( , , )
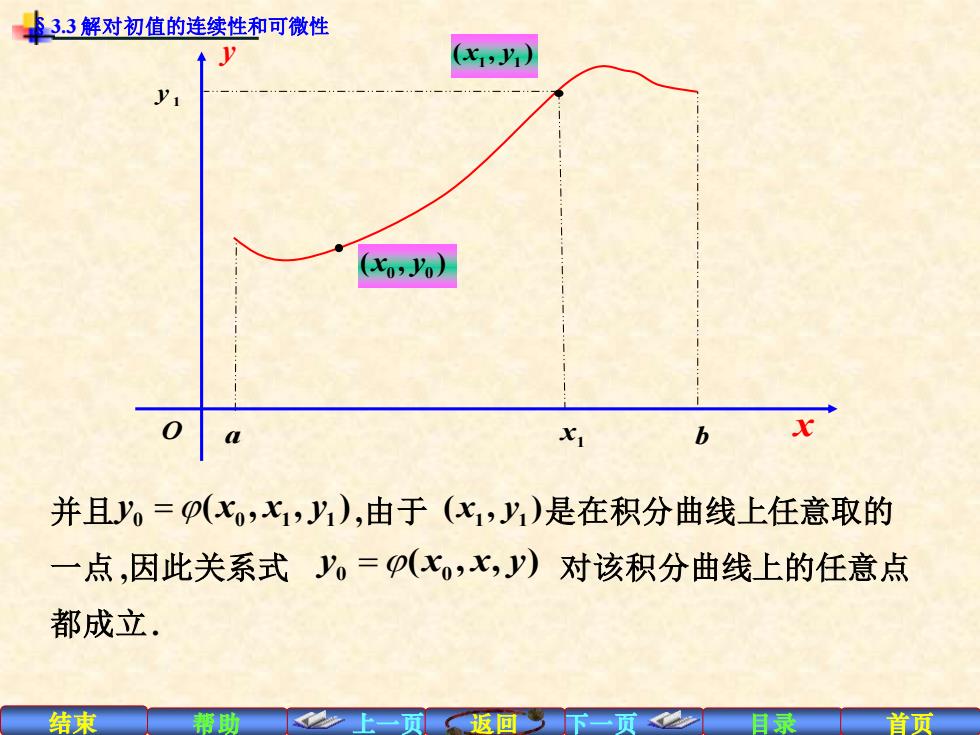
33解对初值的连续性和可微性 (y1) (xo2Yo) XI b 并且J=(xo,x1,1),由于(x1,y1)是在积分曲线上任意取的 一点,因此关系式'=(xo,x,)对该积分曲线上的任意点 都成立. 结束 帮助 返
结束 帮助 上一页 返回 下一页 目录 首页 并且 ,由于 是在积分曲线上任意取的 一点 ,因此关系式 对该积分曲线上的任意点 都成立. y x x y 0 0 1 1 =( , , ) 1 1 ( , ) x y y x x y 0 0 =( , , ) 1 y 1 1 ( , ) x y O a x1 b 0 0 ( , ) x y y x §3.3 解对初值的连续性和可微性

33解对初值的连续性和可微性 引理.如果函数f(x,y在某域D内连续,且关于y满足 Lipschitzz条件(Lip常数为L),则对(2.1)的任意两个解p(x)及(r), 在它们公共存在的区间内成立着不等式 o(x)-(x)(x)-(x)ex 其中x为所考虑区间内的某一值。 证明:设p(x),(x)的公共存在区间为[a,b],令 V(x)=(p(x)-(x)),xEla,b] ◆V'(x)=2(p(x)-(x)(p'(x)-'(x) =2(p(x)-(x)(f(x,p(x)-f(x,p(x)) ≤2L(p(x)-(x)=2LV(x) →V'(x)-2LV(x)≤0,两边乘e-2Lx:V'(x)e2-2Le2V(x)≤0 d(V(x)e2) ≤0 dx 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 引理. 如果函数 在某域 内连续,且关于 满足 Lipschitz条件(Lip常数为L) ,则对(2.1)的任意两个解 及 , 在它们公共存在的区间内成立着不等式 f x y ( , ) D y ( ) x ( ) x 0 0 0 ( ) ( ) ( ) ( ) L x x x x x x e − − − = − ( ) 2 V x x x x a b ( ) ( ) ( ) , [ , ] = − − 2 ( ) ( ) ( , ( )) ( , ( )) ( x x f x x f x x )( ) 0 其中 x 为所考虑区间内的某一值。 证明:设 ( ) x , ( ) x 的公共存在区间为 [ , ] a b ,令 V x x x x x ( ) 2 ( ) ( ) ( ) ( ) = − − ( )( ) §3.3 解对初值的连续性和可微性 ( ) 2 − = 2 ( ) ( ) 2 ( ) L x x LV x − V x LV x ( ) 2 ( ) 0 −2Lx e − − − 2 2 ( ) 2 ( ) 0 Lx Lx ,两边乘 : V x e Le V x ( ) − 2 ( ) 0 Lx d V x e dx