
常微分方程多媒体教学课件 第二章:一阶微分方程的初等解法 ○第一节变量分离方程与变量变换 ○第二节线性方程与常数变易法 ○第三节恰当方程与积分因子 第四节一阶隐方程与参数表示 。总结 ○本章重点与难点 测试题 结束 帮助 返回下一顶<2 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 第二章:一阶微分方程的初等解法 常微分方程多媒体教学课件 第一节 变量分离方程与变量变换 第二节 线性方程 与常数变 易法 第三节 恰 当 方 程与 积分 因 子 第四节 一阶隐方程 与 参数表示 本章重点与难点 总结 测试题

第二章一阶微分方程的初等解法 本章介绍一阶方程的初等解法。初等解法也称为初等积 分法。之所以称为初等积分法,是因为这样解法最后都 把求解的问题化成求积分,并将方程的通解用初等函数 或它的积分表达出来。凡是能做到这一点的常微分方程, 称为可积方程。并不是所有的一阶微分方程都是可积的, 即一般的微分方程它没有初等解法。这一章将介绍若干 个可积方程的解法。这些内容虽然简单,但都是常微分 方程求解的基本方法。 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 第二章 一阶微分方程的初等解法 • 本章介绍一阶方程的初等解法。初等解法也称为初等积 分法。之所以称为初等积分法,是因为这样解法最后都 把求解的问题化成求积分,并将方程的通解用初等函数 或它的积分表达出来。凡是能做到这一点的常微分方程, 称为可积方程。并不是所有的一阶微分方程都是可积的, 即一般的微分方程它没有初等解法。这一章将介绍若干 个可积方程的解法。这些内容虽然简单,但都是常微分 方程求解的基本方法

§2.1变量分离方程与变量变换 一.分离变量法 例2.1 例2.2 例2.3 例2.4 二.可化为变量分离方程的方程 例2.5 例2.9 例2.6 例2.10 例2.7 例2.11 例2.8 结束 上一版下而 首页
结束 帮助 上一页 返回 下一页 目录 首页 §2.1 变量分离方程与变量变换 一.分离变量法 二.可化为变量分离方程的方程 例2.1 例2.2 例2.5 例2.3 例2.4 例2.6 例2.9 例2.10 例2.8 例2.7 例2.11
§2.1变量分离方程与变量变换 讲授内容: 1.变量分离方程及其求解方法 2.可化为变量分离的方程 教学要求: 掌握一解变量分离方程求解方法;掌握齐 次方程求解方法. 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 §2.1 变量分离方程与变量变换 1.变量分离方程及其求解方法. 2.可化为变量分离的方程. 掌握一解变量分离方程求解方法;掌握齐 次方程求解方法. 讲授内容: 教学要求:
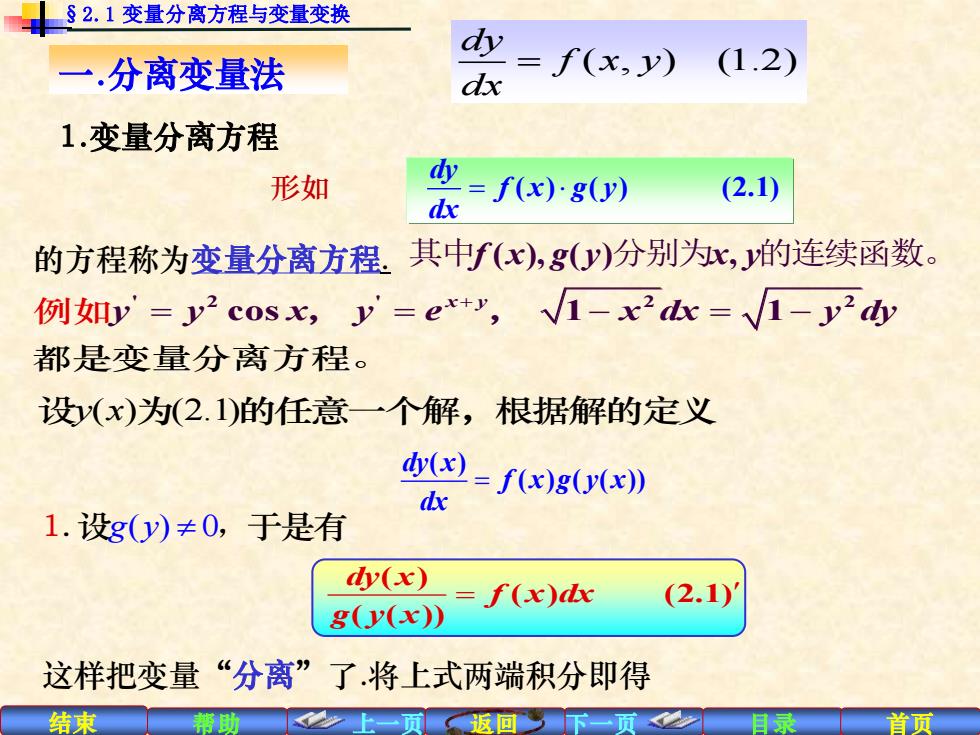
§2.1变量分离方程与变量变换 dy 一.分离变量法 dx .=f(x,y) (1.2) 1.变量分离方程 形如 =f(x)80) d (2.1) 的方程称为变量分离方程。其中f(x),g()分别为r,的连续函数。 例y'=y2cosx,y'=e*+",√1-x2dx=√1-y2y 都是变量分离程。 设(x)为(2.1)的任意一个解,根据解的定义 (x d 2=fx)g(0(x》 1.设g(y)≠0,于是有 dy(x) (2.1) g(v(x)) =f(x)dx 这样把变量“分离”了.将上式两端积分即得 结束 帮助 2一贡返回下页<之 首页
结束 帮助 上一页 返回 下一页 目录 首页 ' 2 ' 2 2 cos 1 1 x y y y x y e x dx y dy + 例如 = = − = − 都是变量分 , , 离方程。 1. 设g y( ) 0 ,于是有 ( ) ( ) (2.1) ( ( )) dy x f x dx g y x = 一.分离变量法 1.变量分离方程 的方程称为变量分离方程. 其中f x g y x y ( ), ( ) , 分别为 的连续函数。 这样把变量“分离”了.将上式两端积分即得 设y x( ) (2.1) 为 的任意一个解,根据解的定义 ( ) ( ) ( ( )) dy x f x g y x dx = §2.1 变量分离方程与变量变换 ( ) ( ) (2.1) dy f x g y dx 形如 = ( , ) (1.2) dy f x y dx =