
导效 方本 4.开区域及闭区域 ·若点集E的点都是内点,则称E为开集; ·E的边界点的全体称为E的边界,记作∂E, ·若点集E一OE,则称E为闭集; ·若集D中任意两点都可用一完全属于D的折线相连 则称D是连通的; ·连通的开集称为开区域,简称区域; ·开区域连同它的边界一起称为闭区域
山东农业大学 高等数学 主讲人:苏本堂 D 4. 开区域及闭区域 • 若点集 E 的点都是内点,则称 E 为开集; • 若点集 E E , 则称 E 为闭集; • 若集 D 中任意两点都可用一完全属于 D 的折线相连 , • 开区域连同它的边界一起称为闭区域. 则称 D 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; 。 。 • E 的边界点的全体称为 E 的边界, 记作E ;
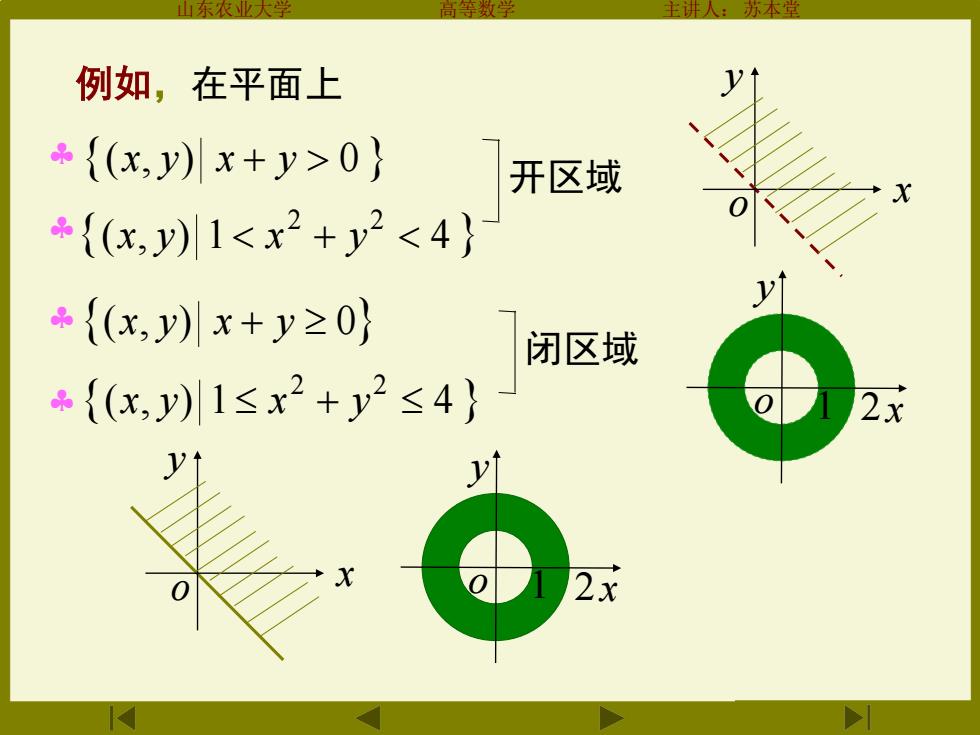
例如,在平面上 {(xy)x+y>0} 开区域 {(x,y)1<x2+y2<4} 1 {(,y)x+y≥0} 闭区域 {(x,y)1≤x2+y2≤4} 2x 2x
山东农业大学 高等数学 主讲人:苏本堂 例如,在平面上 (x, y) x + y 0 ( , ) 1 4 2 2 x y x + y (x, y) x + y 0 ( , ) 1 4 2 2 x y x + y 开区域 闭区域 x y o 1 2 x y o x y o x y o 1 2

主计 苏本堂 整个平面是最大的开域, 也是最大的闭域; 点集{(x,y)川x>}是开集, 但非区域 ·对区域D,若存在正数K,使一切点P∈D与某定点 A的距离AP飞K,则称D为有界域,否则称为无 界域
山东农业大学 高等数学 主讲人:苏本堂 整个平面 点集 (x, y) x 1 是开集, 是最大的开域 , 也是最大的闭域; 但非区域 . −1 o 1 x y • 对区域 D , 若存在正数 K , 使一切点 PD 与某定点 A 的距离 AP K , 则称 D 为有界域 , 界域 . 否则称为无

5.n维空间 n元有序数组(1,x2,.,xn)的全体称为n维空间, 记作R”,即 Rn=RxRX.xR ={(,2,.,xnk∈R,k=1,2,.,n} n维空间中的每一个元素(x1,x2,.,xn)称为空间中的 一个点,数x称为该点的第k个坐标 当所有坐标x=0时,称该元素为R”中的零元,记作
山东农业大学 高等数学 主讲人:苏本堂 5. n 维空间 n 元有序数组 的全体称为 n 维空间, R , n n 维空间中的每一个元素 称为空间中的 称为该点的第k 个坐标 . 记作 即 R = R R R n 一个点, 当所有坐标 称该元素为 n R 中的零元,记作 O