《复变函数与积分变换》课程教学资源（PPT课件）第一章 复数与复变函数 1.0 习题课

复变函数（3）三角表示法x = rcoso.利用直角坐标与极坐标的关系y=rsine,复数可以表示成z=r(cos+isine)(4）指数表示法利用欧拉公式 eio=cosの+isinの,z=reie复数可以表示成称为复数z的指数表示式u

11 （3）三角表示法 利用欧拉公式 cos sin ,  e i i = + 复数可以表示成 i z = re 称为复数 z 的指数表示式. （4）指数表示法 利用直角坐标与极坐标的关系    = = sin , cos ,   y r x r 复数可以表示成 z = r(cos + isin )

复变函数4.复数的乘幂与方根1）乘积与商两个复数乘积的模等于它们的模的乘积；两个复数乘积的辐角等于它们的辐角的和若z=ri(cos +isin),Z2 = r2(cos0, +isin0,),则有z · z2 = ri · r[cos(0 +0,) + isin(0 +0)]Arg(z,z2) = Argzi + Argz2.U

12 4.复数的乘幂与方根 1) 乘积与商 两个复数乘积的模等于它们的模的乘积; 两个复数乘积的辐角等于它们的辐角的和. (cos sin , 若 z1 = r1 1 + i 1） (cos sin , z2 = r2  2 + i  2） [cos( ) sin( )] 1 2 1 2 1 + 2 + 1 + 2 z z = r r i Arg( ) Arg Arg . 1 2 1 2 z z = z + z 则有

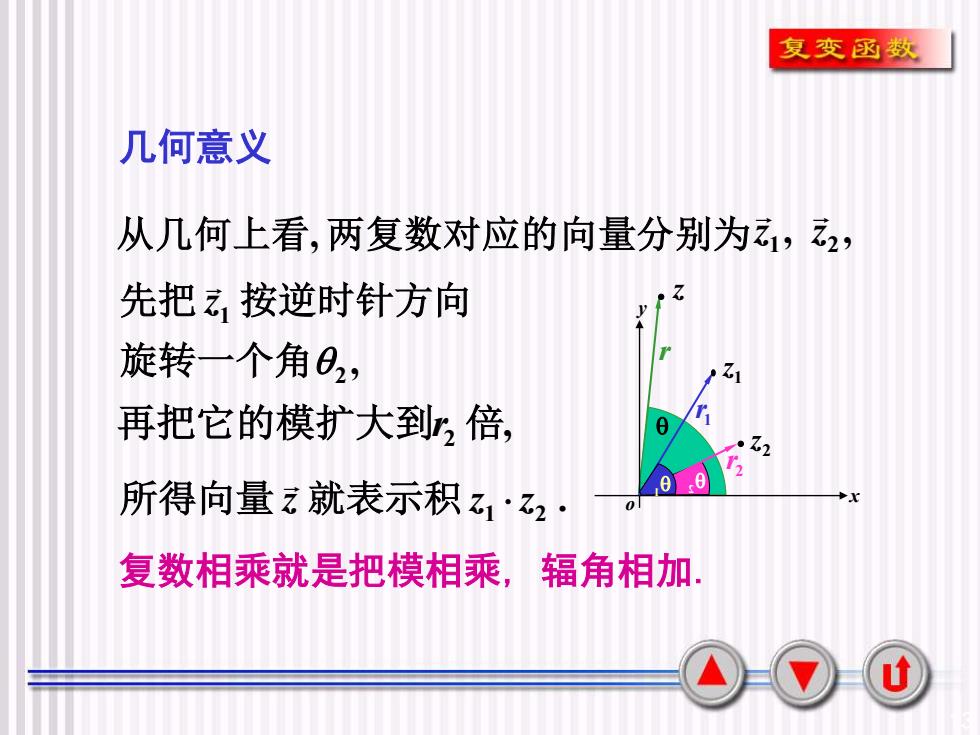
复变函数几何意义从几何上看，两复数对应的向量分别为，Z先把按逆时针方向旋转一个角02:Z12r再把它的模扩大到r,倍A·Z210O所得向量之就表示积Z·z2·X0辐角相加复数相乘就是把模相乘u

13 几何意义 复数相乘就是把模相乘, 辐角相加. , 再把它的模扩大到r2 倍 从几何上看, 两复数对应的向量分别为 , , 1 2 z z   , 2 1 旋转一个角 先把 z 按逆时针方向  . 1 2 所得向量 z 就表示积 z z   2  o x y r 2r 1r • 2 z 1  • 1z • z

复变函数两个复数的商的模等于它们的模的商：两个复数的商的辐角等于被除数与除数的辐角之差若Zi = ri(cose, +isine),z2 = r2(cos0, + isin e,)则有5Z2Z2Arg= Argz2 - ArgziZ1Z12.1设复数z,和z的指数形式分别为2i(02-0)则2Zi = rieio,Z2 = reio,，2rZ1U

14 两个复数的商的模等于它们的模的商; 两个 复数的商的辐角等于被除数与除数的辐角之差. , 1 2 1 2 z z z z = Arg Arg Arg . 2 1 1 2 z z z z  = −      设复数z1和z2的指数形式分别为 , 1 1 1 i z = r e . ( ) 1 2 1 2  2−1 = i e r r z z z2 = r2 e i 2 , 则 (cos sin , 若 z1 = r1 1 + i 1） (cos sin , z2 = r2  2 + i  2） 则有

复变函数2)幂与根(a) n次幂:n个相同复数z的乘积称为z的n次幂记作z"，"=n个对于任何正整数n,有 zn =rn(cos ne+isinnの)n为负整数时，有z-n=t因而有z"=z",Argz" = nArgz.U

15 2) 幂与根 (a) n次幂: , , n z n z z n 记作 个相同复数 的乘积称为 的 次幂  . n个 n z = zz z n, z r (cos n isin n ). n n 对于任何正整数 有 = + . 1 , n n z n z = 为负整数时 有 − z z , Arg z nArg z. n n n 因而有 = =