
复变函数4)共轭复数实部相同而虚部绝对值相等符号相反的两个复数称为共轭复数与z共轭的复数记为z,若z=x+iv,则z=x-iy共轭复数的性质Z一2(1) Z ± Z2 = Z ± ; Z : Z2 = Z Z2 ;(2) z = z; ;(3) z·z=[Re(z)} +[Im(z)};(4) z + z = 2Re(z),z-z = 2iIm(z)u
6 4)共轭复数 与z 共轭的复数记为z, 若 z = x + iy, 则 z = x − iy. 实部相同而虚部绝对值相等符号相反的两 个复数称为共轭复数. 共轭复数的性质 (1) ; 1 2 1 2 z z = z z ; 1 2 1 2 z z = z z ; 2 1 2 1 z z z z = (2) z = z; (3) Re( ) Im( ) ; 2 2 zz = z + z (4) z + z = 2Re(z), z − z = 2iIm(z)

复变函数3.复数的其它表示法(1)几何表示法复数z=x+i与有序实数对(x,y)成一一对应.因此,一个建立了直角坐标的平面可以用来表示复数,通常把横轴叫实轴或x轴,纵轴叫虚轴或√轴.这种用来表示复数的平面叫复平面.yz=x+iy1(x,y)复数z=x+i可以用复平面上的点(x,J)表示xX0U
7 3.复数的其它表示法 . . , , . , ( , ) 面 叫虚轴或 轴 这种用来表示复数的平面叫复平 用来表示复数 通常把横轴叫实轴或 轴 纵 轴 对 应 因 此 一个建立了直角坐标系的平面可以 复 数 与有序实数对 成一一 y x z = x + iy x y 面上的点( , )表示. 复数 可以用复平 x y z = x + iy (x, y) x y x y o z = x + iy (1)几何表示法
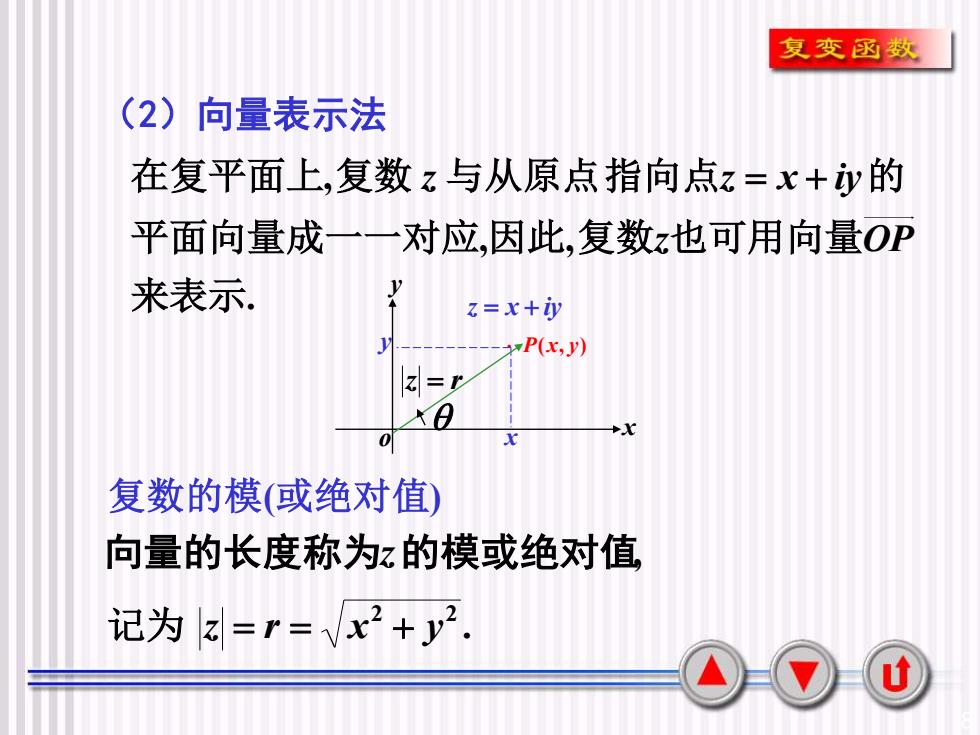
复变函数(2)向量表示法在复平面上,复数z与从原点指向点z=x+i的平面向量成一一对应,因此.复数z也可用向量OPy来表示z=x+iyyP(x,y)z=rNA+xx0复数的模(或绝对值)向量的长度称为的模或绝对值记为z=r=x2+2u
8 (2)向量表示法 . , , , 来表示 平面向量成一一对应 因此 复数 也可用向量 在复平面上 复数 与从原点指向点 的 z OP z z = x + iy P(x, y) x y x y o z = x + iy z = r 复数的模(或绝对值) 向量的长度称为z的模或绝对值, . 2 2 记为 z = r = x + y

复变函数模的性质[≤,≤+,·==x≤z,三角不等式(1)+z2≤+;(2) -z2≥-2复数的辐角在z≠0的情况下,以正实轴为始边以表示Z的向量OP为终边的角的弧度数称为z的辐角记作 Argz=.当z=0时,lz=0,而辐角不确定任何一个复数z≠0有无穷多个辐角如果θ是其中一个辐角 那么z的全部辐角为Argz=, +2k元(k为任意整数)u
9 模的性质 x z, y z, z x + y , . 2 2 zz = z = z (1) ; 1 2 1 2 z + z z + z (2) . 1 2 1 2 三角不等式 z − z z − z 复数的辐角 当 z = 0 时, z = 0, 而辐角不确定. 任何一个复数 z 0有无穷多个辐角. , 如果1 是其中一个辐角 那么 z 的全部辐角为 Arg 2 π ( ). z =1 + k k为任意整数 Arg . , 0 , , = z z OP z z 记 作 的向量 为终边的角的弧度数 称 为 的辐角 在 的情况下 以正实轴为始边 以表示

复变函数辐角的主值在z(≠0)的辐角中,把满足一元<≤元的称为Argz的主值,记作。=argz.x>0,arctanxZ±0π-2+x =0, y± 0,辐角的主值argz=V二±元,x<0,y±0,arctanxx<0,y= 0.元,元.12y(其中/arctan2xU
10 Arg , arg . ( 0) , π π 0 0 0 z z z = − 称为 的主值 记作 在 的辐角中 把满足 的 = = = , 0, 0. arctan , 0, 0, , 0, 0, 2 arctan , 0, arg x y x y x y x y x x y 辐角的主值 z z 0 ) 2 arctan 2 ( − x y 其中 辐角的主值